Деление отрезков в данном отношении.

Дано: произвольный отрезок М₁М₂ и пусть М-произв. точка этого отрезка, отличная от М₂. Число - отношение, в к-ром М делит отрезок М₁М_2.

_{Теорема:} Если делит отрезок М₁М₂ в отнош. l, то корд. этой точки определяются рав-вом , где -коорд. М₁, -М₂.

Док-во:Докажем 1 из формул: 1) х₁=х₂=х=х₁*(1+λ)/1+ λ=( х₁+ λ х₁)/1+ λ=

2) х₁ не=х₂,опустим перпендикуляры из т.М,М₁,М₂ на ось ОХ и обозначим их Р,Р₁,Р₂,по теореме о пропорциональности отрезков ММ1/ ММ₂= РР₁/ РР₂=λ; РР₁= / х- х₁/; РР₂ =/ х₂- х/

Эти выражения имеют один и тот же знак.неогранич. общности будем считать,что эти выражения положительны,тогда: / х- х₁/ / /х₂- х/=λ,выражаем х=

Следствие:еслитМ-середина отрезка М₁М₂,то её координаты (х₁+х₂)/2 и аналогич. У

Площадь треугольника.

Т. Для любых точек не лежащих на одной прямой, выражается ф-лой

3)Ур-ние прямой на плоскости

Пусть на плоскости задана прямоуг. с-ма координат и нек-рая линия .

О. Ур-ние вида связывающее переменные 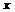и 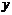наз-тсяур-нием линии (в заданной с-ме координат); если этому ур-нию удовлетворяют координаты любой точки, лежащей на линии и не удовлетворяют координаты никакой другой точки, не лежащей на линии .

Примеры ур-ний линий на плоскости.

1. Рассм. прямую параллельную оси Оу. Обозначим буквой А точку пересечения А с Ох. Точка А(а,0).

Ур-ние х=а явл. ур-нием данной прямой, т.к. этому ур-нию удовлетворяют координаты любой точки М(а,у) и не удовлетворяют координатам ни одной точки не лежащей на этой прямой. Если а=0, то прямая совпадает с осью Оу.

2. Ур-ние определяет множ-во точек плоскости, составляющих биссектрисы 1-го и 3-го координатных углов.

3. . Данноеур-ние задает множ-во точек на плоскости, составляющих биссектрисы коорд. углов.

4. . Это ур-ние задает единственную точку на плоскости с коорд (0,0). . Это ур-ние с центром в точке (0,0)

Ур-ниепрямой с угловым коэффициентом.

Пусть прямая, не параллельная оси Оу.

Обозначим точки пересечения с Оу точкой В, а угол между полож. направлением оси Ох и обозначим j .Ðjназ-тся углом наклона к Ох (и в пределах от [0;p) ). Пусть М(х,у)- произвольная точка прямой. Величину обозначают и называют угловым коэффициентом прямой. Тогда ур-ние примет вид –ур-ние прямой с угловым коэффициентом, в частности если =0, то j=0, прямая параллельна оси Ох. с ур-нием если =0 и получаем ур-ние оси Ох.

Уравнение прямой по 2 точкам.

Пусть данная прямая имеет угловой коэф. и проходит через точку . Искомое ур-ние прямой . Подставим коорд. точки М₁в ур-ние

Ур-ние прямой, проходящей через 2 данные точки.

Пусть искомая прямая проходит через точки и . Искомое ур-ние , где и неизвестны. Т.к. прямая проходит через М₁, то , т.к. прямая проходит через М₂, то . Выразим из первого ур-ния и подставим во второе

Пр. Составить ур-ниепрямой по точкам (1;2);(2;4)

Общее ур-ниепрямой.

Т. Каждая прямая на плоскости с прямоуг. с-мой корд.определяется ур-нием первой степени , где α и b одновременно не равны 0. a² + b² ≠0 определяет нек-рую прямую на плоскости.

Док-во:Пусть прямая имеет ур-ние ,тогда кх-у+b,тоесть А=к,В=-1,С=b,следовательно Ур-ние прямой удовлетворяет общему виду Ур-ний;

Обратно если прямая задается этим урачнение,по условию хотябы один из коэффициентов отлтченотнуля делим на этот коэффициент,и получаем прямую которая соответствует Ур-нию с угловым коэффициентом.

Это ур-ние называют общим ур-нием прямой на плоскости.