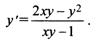Производная алгебраической суммы функций, произведения и частного.

Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих

функций, т.е.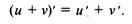

Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.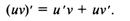

Производная частного двух дифференцируемых функций может быть найдена по формуле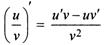

Общая схема нахождения производных функций.

Производная функции у =f(x) может быть найдена по следующей схеме:

1. Дадим аргументу х приращение 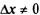и найдем наращенное значение функции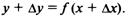

2. Находим приращение функции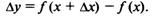

3. Составляем отношение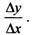

4. Находим предел этого отношения при 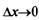, т.е.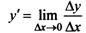

(это не к вопросу, но знать нужно)

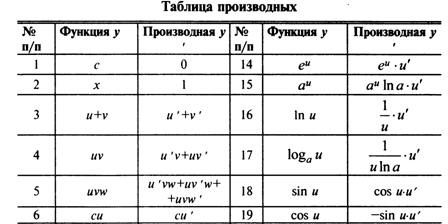
Правило дифференцирования сложной функции.

Пусть переменная у есть функция от переменной 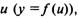а переменная u в свою очередь есть функция от независимой переменной х:, т.е. задана сложная функция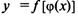

Теорема. Если 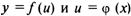— дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного

аргумента по независимой переменной х, т.е.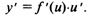

Правило дифференцирования сложной функции может

быть записано и в других формах: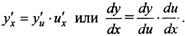

Логарифмическое дифференцирование.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для н𝜟хождения производных степенных, рациональных и некоторых иррациональных функций.

Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

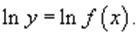
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

Отсюда видно, что искомая производная равна

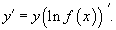
Такая производная от логарифма функции называется логарифмической производной.

Данный метод позволяет также эффективно вычислять производные показательно-степенных функций, то есть функций вида

где u(x) и v(x) − дифференцируемые функции от x.

Дифференцирование неявных функций.

Рассмотрим дифференцирование неявной функции, заданной урав-

нением F{x, у) = 0

Для нахождения производной функции у, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от х, а затем из полученного уравнения найти производную у'.

Найти производную функции у, заданной уравнением 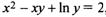, и вычислить ее значение в точке (2; 1).

Решение. Дифференцируя обе части равенства и учитывая,

что у есть функция от х, получим 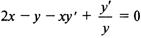, откуда