Транспонирование и эрмитово сопряжение

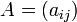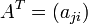Транспонирование уже обсуждалось выше: если , то . Для комплексных матриц более употребительно эрмитово сопряжение: 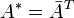. С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряжённая матрица — это матрицы оператора, сопряжённого относительно скалярного или эрмитова произведения, соответственно.

След

Основная статья: След матрицы

Для квадратной матрицы определен след:

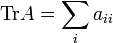
(иногда также обозначается как Sp или Spur).

Является инвариантом ортогональных (унитарных) преобразований матрицы, соответствующих преобразованию матричного представления линейного оператора или билинейной (квадратичной) формы при соотвестствующем преобразовании векторного пространства (например, вращении).

Определитель (детерминант)

Основная статья: Определитель

Перманент

Основная статья: Перманент

Линейные трансформации

Основные статьи: Линейная трансформация, Трансформация матрицы

Векторы представлены как матрица 2 x 2, образованная сторонами соответствующего единичного квадрата, трансформируемого в параллелограмм.

Матрицы и их произведения выявляют их существенные особенности, когда это связано с линейными преобразованиями, так же известными, как линейные карты. Матрица A вещественных чисел размера m × n порождает линейное преобразование Rⁿ → R^m отображая каждый вектор x в Rⁿ на новую матрицу Ax, которая является вектором R^m. Наоборот, каждое линейное преобразование f: Rⁿ → R^m вытекает из уникальной m × n матрицы A: явно (i, j)-вхождение матрицы A есть i-тая координата f(e_j), где e_j = (0,...,0,1,0,...,0) является единичным вектором с единицей в j-той позиции и 0 в остальных случаях. Матрица A как говорят, представляет собой линейную карту f, и называется матрицей трансформирования f.

Для примера матрица 2×2

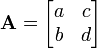
может быть рассмотрена при трансформации единичного квадрата в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d). Параллелограмм, показанный на рисунке справа получается путем умножения матрицы A на каждый вектор-столбец 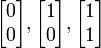и . Эти векторы определяют вершины единицы площади.

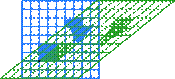
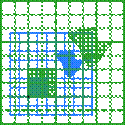
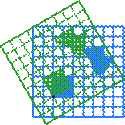
В следующей таблице показаны матрицы 2 × 2 вещественных чисел с соответствующими им линейными картами R². Синим цветом обозначена исходная карта, а зеленым - трансформированная and shapes. Начало (0,0) обозначено черной точкой.

Горизонтальный сдвиг (m=1.25)	Горизонтальный поворот	Сжатие (r=3/2)	Масштабирование (3/2)	Поворот (π/6R = 30°)

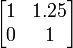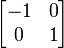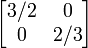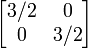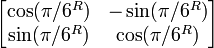Связанные понятия

Линейные комбинации

В векторном пространстве линейной комбинацией векторов 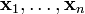называется вектор

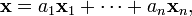
где 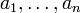— коэффициенты разложения:

• если все коэффициенты равны нулю, то такая комбинация называется тривиальной,
• если же хотя бы один коэффициент отличен от нуля, то такая комбинация называется нетривиальной.

Это позволяет описать произведение 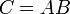матриц и 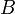терминах линейных комбинаций:

• столбцы матрицы 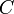— это линейные комбинации столбцов матрицы с коэффициентами, взятыми из матрицы ;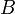
• строки матрицы 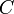— это линейные комбинации строк матрицы 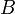с коэффициентами, взятыми из матрицы .

Линейная зависимость

Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.

Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или

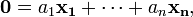
где не все числа 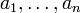равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.

Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.

Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:

• если строки матрицы 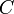линейно зависят от строк матрицы 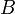, то 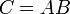для некоторой матрицы ;
• если столбцы матрицы 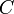линейно зависят от столбцов другой матрицы , то 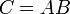для некоторой матрицы .

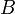Ранг матрицы

Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.

Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

Свойства

Матричные операции

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица 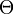такая, что её прибавление к другой матрице A не изменяет A, то есть

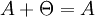
Все элементы нулевой матрицы равны нулю.

Возводить в степень можно только квадратные матрицы.

• Ассоциативность сложения:
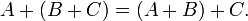
• Коммутативность сложения:
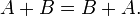
• Ассоциативность умножения:
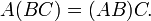
• Вообще говоря, умножение матриц некоммутативно: 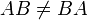. Используя это свойство, вводят коммутатор матриц.
• Дистрибутивность умножения относительно сложения:

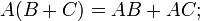
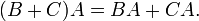
• С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
• Свойства операции транспонирования матриц:

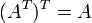
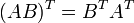
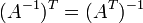, если обратная матрица 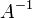существует.

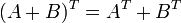
Примеры

Основная статья: Список матриц