Безусловный и условный экстремумы функций двух переменных.

Безусловный экстремум.

z=f(x,y) (x,y) ∈D U – окрестность (x0,y0)

Точка (x0,y0) ∈D называется точкой локального минимума (максимума) функции z=f(x,y), если найдется такая окрестность точки (x0,y0), что f(x0,y0)<= (x,y) любая (x,y)∈U. Значения в этих точках называются loc min (loc max).

Точки loc min (loc max) – точки локального экстремума.

Теорема 1. Если (x0,y0)∈D – точка лок экстремума и ф-ция z=f(x,y) дифференцируема в точке (x0,y0), то ∂f(x0,y0)/∂x=∂f(x0,y0)/∂у=0. Еще такие точки называют стационарными.

Теорема 2.Пусть (x0,y0) – стационарные точки ф-ции z=f(x,y) и пусть в окрестностях точки (x0,y0) ф-ции z=f(x,y) дважды дифференцируема, обозначим

а₁₁=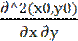

а₁₂= 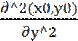=a₂₁

_∆=

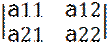
1. Если ∆>0 – точка (x0,y0) точка лок экстремума (а₁₁>0-лок мин_, а₁₁<0-лок макс)

2. ∆<(x0,y0) нет лок экстремума

3. ∆=0 лок экстремум может сущ, а может и не сущ.

Условный экстремум.

z=f(x,y) (x,y)∈D Х∈D

Х={(x,y) ∈R² : g_i (x,y)=0, i=1,k}

Ф-ция g_i – уравнение связи

а) (x0,y0)∈Х – точка условного мин (макс) ф-ции z=f(x,y, если найдется такая окрестность точки (x0,y0), что f(x0,y0)<= f(x,y).

Точки условного мин (макс) - точки условного экстремума.

Для исследования экстрим значений ф-ции на множестве Х, задачу поиска условнго экстремума заменяют задачей поиска условного экстремума для ф-ции Лагранжа L(x,y,z)=f(x,y)+δ_i+1, λ_ig_i(x,y), λ(λ1,…, λk) множители Лагранжа

Метод Лагранжа:

1. Составляем ф-цию Лагранжа

2. Ищем условную стационарную точку

3. Исследуем хар-р найденного условия, используя второй дифференциал ф-ции Лагранжа (если больше 0 – точка условного мин и наоборот)

Площадь фигуры и объем тела.

Площадь фигуры

Рассмотрим множество точек плоскости R². Фигурой будем называть любое подмножество множества R². Множество P = [a,b] Х [c,d] ⊂ R² является прямоугольником. Площадь прямоугольника P равна S_P = (b − a)(d − c).

Элементарной фигурой D ⊂ R2 назовем фигуру, составленную из конечного числа прямоугольников, каждые два из которых не имеют общих внутренних точек.

Площадь элементарной фигуры равна сумме площадей прямоугольников, составляющих эту фигуру,

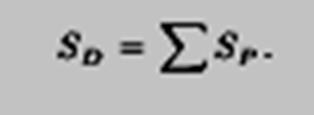
Элементарные фигуры D_∗ и D^∗ называют, соответственно, вписанной и описанной для фигуры F, если D_∗⊂F⊂D^∗.

Число S_∗, равное супремуму площадей элементарных фигур, вписанных в фигуру F, называют внутренней площадью фигуры F:

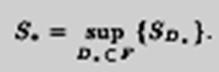
Аналогично, S∗ = inf_F⊂D^∗{SD^∗} – внешняя площадь фигуры F.

Фигура F ⊂ R2 называется квадрируемой, если ее внешняя S^∗ и внутренняя S_∗ площади равны. При этом число S = S_∗ = S^∗ называется площадью фигуры F.

Объем тела

Рассмотрим множество точек пространства R³. Телом будем называть любое подмножество множества R³. Множество P = [a,b]х[c,d]х[g,h]⊂R³ является прямоугольным параллелепипедом (коротко – параллелепипедом). Объем параллелепипеда P равен

VP = (b − a)(d − c)(h − g).

Элементарным телом D ⊂ R³ назовем тело, составленное из конечного числа параллелепипедов, каждые два из которых не имеют общих внутренних точек.

Объем элементарного тела равна сумме объемов параллелепипедов, составляющих это тело

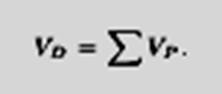
Элементарные тела D_∗ и D^∗ называют, соответственно, вписанным и описанным для тела F, если D_∗⊂F⊂D^∗.

Число V∗, равное супремуму объемов элементарных тел, вписанных в тело F, называют внутренним объемом тела F:

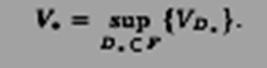
Тело F ⊂ R3 называется кубируемым, если его внешний V ∗ и внутренний V∗ объемы равны. При этом число

V = V _∗ = V^∗ называется объемом тела F.