Оценка среднего квадратического отклонения
Несмещенная оценка среднего квадратического отклонения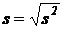 
.
Оценка средней квадратической погрешности среднего арифметического
Оценка среднеквадратической погрешности среднего арифметического вычисляется по формуле: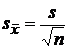 
.
При решении задач на вычисление оценок дисперсий расчеты удобно проводить в таблице.
Интервальные оценки
Интервальной оценкой называется множество точечных оценок, которое зависит от результатов наблюдений и, следовательно, является случайным. Интервальной называется оценку, которая определяется двумя числами – концами интервала. Поэтому каждой интервальной оценке ставится в соответствие доверительная вероятность или надежность, с которой эта оценка накроет неизвестный параметр. В качестве надежности берут число близкое к единице.
Вероятность того, что интервал (Q*-d, Q*+d) заключает в себе (покрывает) неизвестный параметр Q, равна p: Р[Q*-d<Q< Q*+d]=p. Доверительным называется интервал (Q*-d, Q*+d), который покрывает неизвестный параметр с заданной надежностью g.
Наиболее часто p равно 0,9; 0,95; 0,99; 0,999. При исследованиях в фармации, медицине и биологии доверительную вероятность принимают равной 0,95.
Нахождение доверительного интервала для оценки m нормального
распределения при неизвестном s. Распределение Стьюдента
Пусть случайная величина Х имеет нормальное распределение, причем s и m неизвестны. По данным выборки можно построить случайную величину Т (ее возможные значения обозначим через t):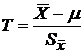 
, где 
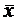– выборочная средняя из n наблюдений; 
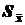– оценка среднего квадратического отклонения выборочной средней (оценка среднеквадратической погрешности среднего арифметического вычисляется по формуле: 
)
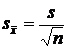Распределение Т с f=n-1 степенями свободы называется t-распределением или распределением Стьюдента. Функция плотности вероятности зависит от числа степеней свободы f и не зависит от дисперсии случайных величин s. Пользуясь распределением Стьюдента можно определить доверительный интервал, покрывающий неизвестный параметр μ с надежностью g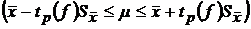 
.
Таким образом, интервальной оценкой математического ожидания является доверительный интервал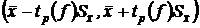 
.
Решение задач
1. Построить полигон относительных частот, если дискретный ряд распределения представлен в таблице:
| хi | |||||||
| mi |
Решение. Найдем объем выборки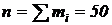 
. Так как относительная частота 
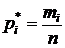, запишем в таблицу полученные значения:
| хi | ||||||||
| mi | ||||||||
| p* | 0,02 | 0,1 | 0,1 | 0,16 | 0,3 | 0,08 | 0,24 | S=1 |
Проконтролируем результат, вычислив сумму полученного ряда (по определению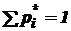 
). Построим полигон относительных частот (рис. 9.3).
2. Результаты наблюдений за числом частиц, попавших в счетчик Гейгера в течение минуты, приведены в виде интервального ряда распределения:
| Интервал Х | 20-24 | 24-28 | 28-32 | 32-36 | 36-40 | 40-44 | 44-48 | 48-52 |
| mi | 1 | 4 | 20 | 10 | 8 | 4 | 2 | 1 |
Построить гистограмму частот распределения.
Решение.
Так как гистограмма это фигура, составленная из прямоугольников с основаниями Dх – длина частичного интервала и высотами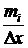 
, то запишем в таблице дополнительную строку 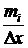. Величина интервала 
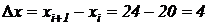, тогда получим таблицу:
| Интервал Х | 20-24 | 24-28 | 28-32 | 32-36 | 36-40 | 40-44 | 44-48 | 48-52 |
| mi | 1 | 4 | 20 | 10 | 8 | 4 | 2 | 1 |
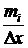| | 0,25 | 1 | 5 | 2,5 | 2 | 1 | 0,5 | 0,25 |
Построим гистограмму (рис. 9.4)
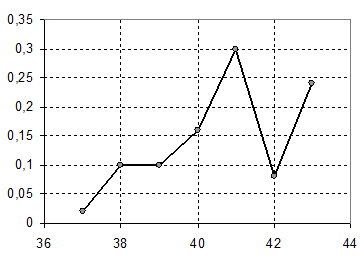
Рис. 9.3
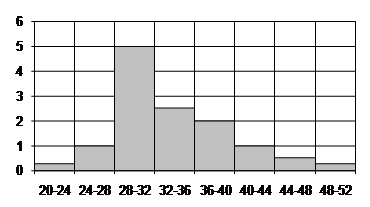
Рис. 9.4.
3. Найти оценку математического ожидания и несмещенную оценку дисперсии, если дана таблица распределения:
| хi | 2 | 4 | 5 | 6 |
| mi | 8 | 9 | 10 | 3 |
Решение. Для вычисления характеристик воспользуемся расчетной таблицей:
| x | m | xm | xв-x | (xв-x)2 | (xв-x)2m |
| -1 | |||||
| -2 | |||||
Оценкой математического ожидания является выборочное среднее – среднее арифметическое значений статистического ряда: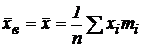 
; итак,
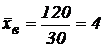. Несмещенная оценка дисперсии генеральной совокупности:
; 
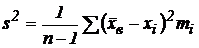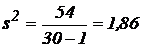
4. Получена выборка значений случайной величины (длина вируса): 0,33; 0,34; 0,32; 0,33; 0,31 (нм). Найти оценку математического ожидания и оценку средней квадратической погрешности выборочного среднего.
Решение. Обратите внимание: другой вариант составления таблицы (без учета повторений)!
| xi |  |  | |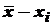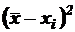
| 0,31 | 0,016 | 0,000256 | |
| 0,32 | 0,006 | 0,000036 | |
| 0,33 | -0,004 | 0,000016 | |
| 0,33 | -0,004 | 0,000016 | |
| 0,34 | -0,014 | 0,000196 | |
| S | 1,63 | 0,00052 |
Найдем среднее арифметическое: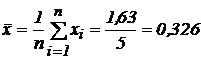 
.
Найдем оценку средней квадратической погрешности среднего арифметического: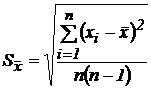 
; 
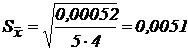(нм).
5. Известно, что количественный признак х генеральной совокупности распределен нормально. По выборке объема n=20 найдены выборочная средняя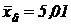 
и несмещенная оценка дисперсии 
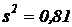. Определить интервальную оценку математического ожидания с доверительной вероятностью р=0,95.
Решение. Доверительный интервал для математического ожидания, в который с вероятностью р попадает m имеет вид: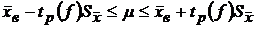 
.
Найдем оценку среднего квадратического отклонения выборочного среднего:
; 
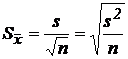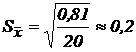. По таблице найдем коэффициент Стьюдента 
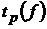. По условию р=0,95, число степеней свободы 
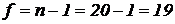. Итак, 
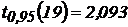. Запишем:
;
.
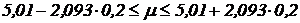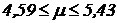Самостоятельная работа студентов на занятии
1. Найти оценку генеральной средней, несмещенную оценку дисперсии и исправленное среднее квадратическое отклонение по выборке: 289; 203; 243; 210; 251; 224; 220; 211; 246. (Указание. Для расчета использовать формулы без учета частот).
2. Время цветения 100 одинаковых растений (в сутках) даны в таблице:
| Фазы цветения | Число цветущих растений (mi) |
| 5-10 | |
| 10-15 | |
| 15-20 | |
| 20-25 | |
| 25-30 | |
| 30-35 | |
| 35-40 |
Построить гистограмму относительных частот распределения фазы цветения. Какой тип распределения напоминает гистограмма.
3. Дана выборка объема n. Найти объем выборки, оценки характеристик распределения, доверительный интервал с вероятностью 0,99, если статистические данные записаны в таблице:
| хi | 0,3 | 0,5 | 0,6 | 0,8 | 0,9 |
| mi | 6 | 10 | 20 | 3 | 1 |
4. В компьютерном классе средствами Excel построить гистограмму распределения для задачи 2, средствами MS Excel решить задачу 3.
Задание на дом
Практика
1. Из генеральной совокупности извлечена выборка:
| хi | 2 | 5 | 7 | 10 |
| mi | 6 | 12 | 8 | 2 |
Найти оценки характеристик распределения. Построить полигон частот.
2. Построить полигон частот и относительных частот по распределению выборки
| хi | 2 | 3 | 5 | 6 |
| mi | 10 | 15 | 5 | 20 |
3. Построить гистограмму относительных частот по распределению выборки
| Интервал Х | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 |
| mi | 2 | 4 | 8 | 4 | 2 |
4. При подсчете количества листьев у одного из лекарственных растений были получены следующие данные: 8, 10, 7, 9, 11,6, 9, 8, 10, 7. Вычислить выборочную среднюю и оценку среднего квадратического отклонения выборочной средней, интервальную оценку с вероятностью 0,95.
Теория
1. Лекция по теме «Погрешности измерений и их оценки. Типы погрешностей. Погрешности прямых и косвенных измерений».
2. Занятие 10 данного методического пособия.
3. Павлушков И.В. и другие стр. 283-288.