Некооперативные игры в сравнении с кооперативными

ОГЛАВЛЕНИЕ

Предисловие……………………………………………………………..

1. Элементы теории игр………………………………………………….

1.1. Основные понятия……………………………………………….

1.2. Матричные игры. Решение матричных игр в чистых стратегиях………………………………………………………..

1.3. Упрощение игр…………………………………………………...

1.4. Решение матричных игр в смешанных стратегиях……………

1.5. Решение задач в смешанных стратегиях. Игра 2×2……………

1.6. Критерии принятия решения в играх с «природой».

1.7. Упражнения………………………………………………………

2. Элементы теории массового обслуживания…………………………

2.1. Структура и классификация систем массового обслуживания.

2.2. Марковский случайный процесс в системах массового обслуживания……………………………………………………

2.3. Уравнения Колмогорова…………………………………………

2.4. Одноканальная система массового обслуживания с отказами..

2.5. Одноканальная система массового обслуживания с очередью.

2.6. Упражнения………………………………………………………

3. Ответы к упражнениям……………………………………………….

4. Библиографический список…………………………………………..

ПРЕДИСЛОВИЕ

Настоящее учебно-методическое пособие предназначено для изучения элементов теории игр и основ теории массового обслуживания.

Работа состоит из двух глав и списка литературы. В первой главе излагаются основные понятия, теоремы и методы решения матричных игр в чистых и смешанных стратегиях, игр с «природой». Во второй главе излагаются основные понятия, формулы и подходы к решению задач по теории массового обслуживания, а именно одноканальные системы массового обслуживания.

Изложение теоретического материала сопровождается подробными решениями примеров. В конце каждой главы приведены упражнения для самостоятельного решения. Библиография, приведенная в конце пособия, может служить путеводителем для более подробного изучения какого-либо из рассматриваемых вопросов.

Элементы теории игр

К задачам теории игр и теории массового обслуживания сводятся многие прикладные задачи экономики.

Подобно линейному программированию теория игр (ТИ) также является одной из современных областей математики. Если при исследовании общей задачи линейного программирования мы определяли способ эффективного использования или распределения ограниченных ресурсов для достижения желаемых целей, то в ТИ нас интересует стратегия, с помощью которой достигается выигрыш, максимально возможный в данной игре. В то время, когда закладывались основы ТИ, замечательное соответствие между этими двумя задачами не было известно. Связь между линейным программированием и ТИ впервые была установлена Джоном фон Нейманом и Данцигом.

Анализ математической стороны и основных принципов ТИ был дан Дж. фон Нейманом в 1928 году. В 1944 фон Нейман и Моргенштерн опубликовали известную работу «Теория игр и экономического поведения», положившую начало бурному развитию математического исследования игр. Эта работа явилась основным толчком для развития линейного программирования и теории статистических решений Вальда. Она открыла также новый подход к задачам выбора решений в конкурентных ситуациях.

Основные понятия

В природе и обществе часто возникают конфликтные ситуации, в которых участвуют стороны с различными или даже противоположными интересами. Конфликтные ситуации возникают при операциях типа купли-продажи (особенно при наличии конкуренции), в судопроизводстве, в спорте и т.д.

Математическая теория конфликтных ситуаций называется ТИ. Задачей ТИ является выработка рекомендаций поведения, которое приводило бы к наибольшей выгоде той или иной стороны.

Методы и рекомендации ТИ разрабатываются применительно к таким специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации ТИ теряют смысл. Чтобы проанализировать конфликтную ситуацию с помощью математических методов ее необходимо упростить, учитывая лишь важнейшие факторы, влияющие на ход конфликта.

Игра – это упрощенная формализованная модель реальной конфликтной ситуации.

Для математического описания игры необходимо четко сформулировать:

· правила игры, в которых должны быть описаны возможные варианты действий игроков;

· объем информации каждой стороны о поведении другой;

· результат игры, к которому приводит каждая совокупность ходов. Этому результату, хотя бы условно, должно быть приписано число, которое называется выигрышем или проигрышем.

Игрок – это одна из сторон в игровой ситуации.

Стратегия игрока – это его правила действия в каждой из возможных ситуаций игр.

Стратегия игрока, обеспечивающая ему максимальный выигрыш, называется оптимальной стратегией этого игрока.

Основная задача ТИ состоит в выявлении оптимальных стратегий игроков.

Конфликтные ситуации, встречающиеся в практике, порождают различные виды игр. Классификацию игр можно проводить по разным признакам. Различают игры:

· по количеству игроков. В игре может участвовать любое конечное число игроков. Если игроки объединяются в две группы, преследующие противоположные цели, то имеет место игра двух «лиц» (парная игра). Например: шахматы – игра двух партнеров с конечным числом возможных ходов; покер – игра многих партнеров с конечным числом возможных ходов.

· В зависимости от взаимоотношений участников различают игры некооперативные и кооперативные.

Решение.

	B1	B2	B3	В4	αi
A1			-1		-1
A2
A3			-2	-1	-2
βj

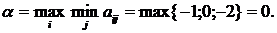
Максиминной чистой стратегией является А₂.

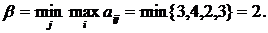
Минимаксной для игрока B является стратегия В₃.

Теорема 1. В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т.е. α ≤ β.

Доказательство:

По определению

,

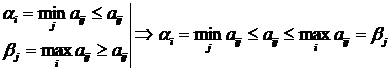значит α_i ≤ a_ij ≤ β_j или α_i ≤ β_j.

Это неравенство справедливо при любых комбинациях i и j. Будет оно справедливо для тех i и j, для которых 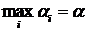и , и 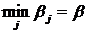при этих i и j получим α ≤ β.

Если в матричной игре нижняя и верхняя чистые цены игры совпадают, т.е. α = β, то это игра имеет седловую точку в чистых стратегиях и чистую цену игры .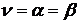

Обозначим через i_* и j_* номера чистых стратегий, при которых имеет место равенство α = β. Пару чистых стратегий 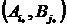игроков А и В, при которых достигается равенство α = β, называют седловой точкой матричной игры, а элемент a_i*j* матрицы, стоящий на пересечении i_* строки и j_* столбца, – седловым элементом платежной матрицы.

Седловой элемент 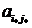является наименьшим в i_* строке и наибольшим в j_* столбце, т.е. 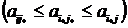. Поэтому, если игрок В отклонится от своей минимальной стратегии, то его проигрыш может увеличиться. Аналогично, отклонение игрока А от своей максимальной стратегии ведет к уменьшению его выигрыша. Таким образом, минимальные стратегии в игре с седловой точкой обладают свойством устойчивости, создают ситуацию равновесия. Следовательно, если в матрице игры существует седловой элемент, то наилучшими для игроков являются их минимальные стратегии. Назовем чистые стратеги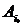и и 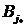, образующие седловой элемент, оптимальными чистыми стратегиями соответственно игроков А и В. Набор 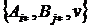назовем решением игры.

Пример. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Предполагают, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируется три возможных варианта выпуска данной модели (А₁, А₂, А₃). Каждый из этих вариантов требует своих затрат и обеспечивает различный эффект. Прибыль (тыс. руб.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей

	I	II	III
A1
A2
A3

Найти объем выпуска модели одежды обеспечивающий среднюю величину прибыли при любом состоянии спроса.

Решение. Проверим, имеет ли исходная матрица седловую точку.

.

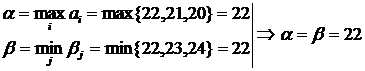Число 22 – цена игры. Игра имеет седловую точку, соответствующую варианту А₁ выпуска модели одежды. Объем выпуска модели, соответствующий данному варианту, обеспечивает прибыль в 22 тыс. руб. при любом состоянии спроса.

Упрощение игр

Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Для игр с платежными матрицами большой размерности отыскание решения можно упростить, если уменьшить их размерность, вычеркивая дублирующие и заведомо невыгодные стратегии.

Если в матрице (a_ij)_m×n игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующие строкам (столбцам) стратегии называются дублирующими.

Если в матрице (a_ij)_m×n игры все элементы некоторой строки, определяющей i-ю стратегию А_i игрока А, не больше (меньше или равны) соответствующих элементов другой строки, то i-я стратегия А_i называется заведомо невыгодной.

Если в матрице (a_ij)_m×n игры все элементы некоторого столбца, определяющего j-ю стратегию В_j игрока В, не меньше (больше или равны) соответствующих элементов другого столбца, то j-я стратегия В_j называется заведомо невыгодной.

Рассмотрим платежную матрицу игры:

B1 B2 B3 В4 В5 αi A1 A2 A3 A4 βj

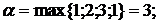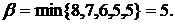α = 3 ≠ β = 5. Платежная матрица игры не имеет седловой точки.

Сравнивая почленно элементы второй и третьей строк, видим, что все элементы второй строки меньше соответствующих элементов третьей строки. Следовательно, вторая стратегия для игрока А заведомо невыгодна и ее можно исключить. Аналогично, сравнивая А₃ и А₄, исключаем А₄. Получаем матрицу игры:

	B1	B2	B3	В4	В5
A1
A3

Замечаем, что 1, 2, 3 стратегии игрока В заведомо невыгодны по сравнению с 5-й стратегией, поскольку игрок В стремится уменьшить выигрыш игрока А. Исключая эти стратегии, получаем матрицу 2×2, в которой нет дублирующих и заведомо невыгодных стратегий.

	В4	В5
A1
A3

Перенумеруем стратегии, запишем платежную матрицу:

В1 В2 αi A1 A2 βj

α = 3, β = 5.

Если для упрощенной матрицы α = β, то число α = β = v есть цена игры не только с упрощенной, но и со сходной матрицей. Если α < β, то анализируется упрощенная матрица, а затем осуществляется возвращение к исходной матрице.

Пример.

В1 В2 αi A1 A2 βj

α = 3, β = 6.

Игрок А может выиграть не менее 3 единиц, а игрок В может ограничить свой проигрыш (выигрыш игрока А) 6 единицами. Область между числами 3 и 6 является как бы нейтральной, и каждый игрок может попытаться улучшить свой результат за счет этой области. А₂ и В₁ – минимаксные стратегии игроков. Если игрок В заметит, что игрок А предпочитает стратегию А₂, то он может использовать стратегию В₂ и уменьшить выигрыш игрока А до 3. Но если игрок А раскроет замысел игрока В и применит стратегию А₁, то он увеличит свой выигрыш до 9. В свою очередь, узнав об этом, игрок В выберет стратегию В₁ и понизит выигрыш игрока А до 2. Таким образом, в очередной партии игрокам надо так выбирать стратегии, чтобы противник о них не догадался, т.е. использовать механизм случайного выбора.

Пусть имеется игра m×n.

Ai Bj	B1	B2	………	Bn	pi
A1	a11	a12	………	a1n	p1
A2	a21	a22	………	a2n	p2
…	…	…	………	…	…
Am	am1	am2	………	amn	pm
qj	q1	q2	………	qn

Обозначим через p₁, p₂, …, p_m вероятности, с которыми игрок А использует чистые стратегии A₁, A₂, …, A_m. Ясно, что

. (*)

Упорядоченное множество (m-мерный вектор), элементы которого удовлетворяют условиям (*), называют смешанной стратегией игрока А. Т.е. смешанной стратегией игрока А является полный набор вероятностей применения его чистых стратегий. Механизм случайного выбора чистых стратегий, которым пользуется игрок А, обеспечивает ему множество смешанных стратегий. Любая чистая стратегия А_i есть частный случай смешанной стратегии , i-ая компонента которой равна 1, а остальные равны 0.

Аналогично упорядоченное множество , элементы которого удовлетворяют соотношениям , является смешанной стратегией игрока В.

Пусть игроки А и В применяют смешанные стратегии и . Это означает, что игрок А использует стратегию А_i с вероятностью p_i, а игрок В – стратегию В_j с вероятностью q_j. Вероятность выбора комбинации стратегий (А_i,В_j) равна P(А_i;В_j) = p_iq_j, при этом будет получен выигрыш a_ij. При использовании смешанных стратегий игра носит случайный характер, случайной становится и величина выигрыша игрока А (проигрыша игрока В). Средняя величина выигрыша (математическое ожидание) является функцией от смешанных стратегий и и определяется:

.

Функция называется платежной функцией игры с матрицей (a_ij)_m×n.

Для решения игры с точки зрения игрока А необходимо найти такие смешанные стратегии и , при которых ему обеспечивался бы средний выигрыш, равный . Эту величину назовем верхней ценой игры .

Аналогичной должна быть ситуация для игрока В: нижняя цена игры .

Оптимальным назовем смешанные стратегии и игроков А и В, удовлетворяющие равенству:

;

– цена игры.

Отметим свойства оптимальных смешанных стратегий.

1) Основная теорема теории игр: любая конечная матричная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно, в смешанных стратегиях.

Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры v.

α ≤ v ≤ β.

2) Для того, чтобы смешанные стратегии и были оптимальными для игроков А и B в игре с матрицей (a_ij)_m×n и ценой v необходимо и достаточно выполнение неравенств:

;

.

3) Пусть и – оптимальные смешанные стратегии игроков А и B в игре I с матрицей (a_ij)_m×n и ценой v. Тогда и будут оптимальными в игре I' с матрицей (ba_ij + c)_m×n, где b>0, и ценой v'=bv+c.

Благодаря этому утверждению любую платежную матрицу можно преобразовать в платежную матрицу, все элементы которой положительны, поэтому цена игры v' также положительна.

1.5. Решение задач в смешанных стратегиях. Игра 2×2

В приведенных формулах для α и β функции min и max вычисляются на бесконечных множествах смешанных стратегий, поэтому значения α и β нельзя найти путем перебора вариантов. Воспользуемся теоремой об активных стратегиях.

Стратегии игроков, входящие в их оптимальные смешанные стратегии, называются активными. В оптимальной смешанной стратегии активными являются стратегии А₂ и А₃.

Теорема 2. Применение оптимальной смешанной стратегии обеспечивает игроку максимальныq средний выигрыш (или минимальный средний проигрыш), равный цене игры v, независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.

Найдем решение в случае игры 2×2. У игроков А и В по две стратегии, игра не содержит седловую точку. Найдем оптимальную смешанную стратегию .

Решение. Матрица игры имеет вид:

Ai Bj	B1	B2
A1	a11	a12
A2	a21	a22

Поскольку игра не имеет решения в чистых стратегиях, в оптимальной стратегии игрока В числа и , т.е. обе стратегии В₁ и В₂ активные. Тогда по теореме об активных стратегиях, если игрок А придерживается своей оптимальной стратегии , то игрок В может, не влияя на значение выигрыша, применять какую-либо из своих чистых активных стратегий В₁ или В₂. Игрок А получит средний выигрыш равный цене игры. Имеем два уравнения:

(при стратегии В₁);

(при стратегии В₂).

Учитывая, что , будем иметь систему трех линейных уравнений с тремя неизвестными. Решив ее, найдем оптимальную смешанную стратегию игрока А и цену игры v. Рассуждая аналогично, для определения оптимальной стратегии игрока В получим систему уравнений:

Пример. Имеются две конкурирующие фирмы А и В, выпускающие однотипные изделия, соответственно видов I и II, которые могут быть окрашены в один из двух цветов: красный (кр.) или синий (син.). Изучение спроса покупателей показало, что если выпущены изделия I кр. и II кр., то 40% покупателей получают I кр. и 60% – II кр. Если выпущены I кр. и II син., то 90% покупателей приобретают I кр. Если изготовлены I син. и II кр. будет продано 70% I син. Если сделаны I син. и II син., то 20% покупателей получат I син.

Найти оптимальные стратегии и цену матричной игры.

Решение. Составим платежную матрицу игры (выигрыш а_ij фирмы А).

A B	II кр.	II син.	αi
I кр.	-20		-20
I син.		-60	-60
βj

– игра не имеет седловой точки.

Найдем оптимальное решение матричной игры в смешанных стратегиях.

Пусть фирма А придерживается своей оптимальной стратегии . По теореме об активных стратегиях, при применении фирмой В чистой стратегии В₁ или В₂ фирма А получит средний выигрыш, равный цене игры, т.е.

Решим систему трех уравнений с тремя неизвестными.

– цена игры.

, v = 10.

Составим систему уравнений для определения оптимальной стратегии игрока В.

Решая систему, найдем .

При таких оптимальных стратегиях изделия фирмы А будут покупать 55%, фирмы В – 45% покупателей (55%+45%=100%).

Упражнения

1. Решить и привести графическую иллюстрацию игр, заданных следующими матрицами:

1.1. . 1.2. .

2. Найти оптимальные стратегии и цену игр, заданных платежными матрицами:

2.1. . 2.2. . 2.3. .

2.4. . 2.5. .

3. Для приведенных ниже платежных матриц вычислить верхнюю и нижнюю цены игры, найти максиминные и минимаксные стратегии, выявить наличие седловых точек. При наличии седловых точек выписать цену игры и оптимальные решения.

3.1. . 3.2. .

3.3. . 3.4. . 3.5. .

4. Для приведенных ниже платежных матриц матричных игр выявить доминирующие строки, доминирующие столбцы и найти для упрощенных матриц α и β. В случае равенства α = β выписать цену игры и оптимальные стратегии не только для упрощенных, но и для исходных матриц.

4.1. . 4.2. . 4.3. .

Уравнения Колмогорова

При анализе случайных процессов с дискретными состояниями пользуются графом состояний, где прямоугольниками изображают состояния системы, а переходы из состояния в состояние – стрелками. Если у стрелок проставлены интенсивности, то граф состояния называется размеченным. Переходы системы из состояния S_i в состояние S_j происходят под воздействием простейших потоков событий с интенсивностями λ_ij.

Простейший граф состояний представлен на рис.1.

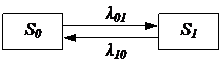
Рис. 1

На рис. 1 изображена СМО, состоящая из одного телефонного аппарата, который находится в двух возможных состояниях: либо свободен (S₀), либо занят (S₁); λ₀₁ – интенсивность нагрузки аппарата, или количество заявок на переговоры в единицу времени; λ₁₀ – интенсивность обслуживания аппаратом, или количество обслуживаемых заявок в единицу времени.

Стрелка из S₀ в S₁ означает переход системы из состояния «аппарат свободен» в состояние «аппарат занят». Стрелка из S₁ в S₀ означает обратный переход.

Анализ состояния СМО сводится к определению вероятности, с которой система пребывает в данном состоянии.

В общем случае вероятностью i-го состояния p_i(t) называется вероятность того, что в момент t система будет находиться в состоянии S_i.

Для любого момента t справедливо соотношение:

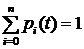, (5)

где n+1 – общее число состояний СМО.

Определить вероятности состояний СМО можно, решив систему уравнений Колмогорова.

Алгоритм составления системы уравнений Колмогорова:

1. В левую часть каждого уравнения ставится производная вероятности i-го состояния по времени.

2. В правую часть каждого управления ставится:

а) сумма произведений вероятностей всех состояний, из которых идут стрелки в i-е состояние, на интенсивности соответствующих потоков событий;

б) минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i-го состояния.

В полученной системе Колмогорова независимых уравнений на единицу меньше их общего числа. Для решения системы добавим уравнение (5).

Задав начальные условия и решив систему дифференциальных уравнений Колмогорова, находят систему функций времени p_i(t), где i – номер состояния. Это позволяет получить дискретное распределение вероятностей СМО для любого момента времени. Для достаточно большого значения времени t независимо от начальных условий распределение вероятностей стабилизируется и практически не зависит от времени.

С неограниченной очередью

Примером одноканальной СМО с неограниченной очередью является одна касса в универмаге.

Пусть поток заявок, поступающих в систему, имеет интенсивность λ, а поток обслуживания – интенсивность μ. Граф состояний подобной системы представлен на рис.3.

Рис. 3

На рис.3 введены следующие обозначения:

состояние S₀ – канал свободен;

состояние S₁ – канал занят, очереди нет;

состояние S₂ – канал занят, одна заявка стоит в очереди; …;

состояние S_k – канал занят, k-1 заявок стоит в очереди и т.д.

Таким образом, на рис.3 представлен процесс гибели и размножения для бесконечного числа состояний.

В общем случае название процесса гибели и размножения связано с биологией и используется для исследования динамики колебаний численности популяций животных, что возможно в рамках теории массового обслуживания. Граф состояний процесса гибели и размножения представлен на рис.4.

Рис. 4

Система алгебраических уравнений для предельных состояний рассматриваемой СМО имеет вид:

Здесь , где p_i(t) – вероятность того, что в момент времени t СМО находится в состоянии S_i.

Решение полученной системы из n+1 уравнений имеет вид:

(10)

Вернемся к одноканальной СМО с неограниченной очередью. При ее анализе полезно знать положение о конечной величине очереди, которое связано с оценкой предельной интенсивности потока заявок . Если в единицу времени среднее число пришедших заявок меньше среднего числа обслуженных заявок, т.е. ρ<1, то предельные вероятности существуют. Если же ρ>1, то очередь растет до бесконечности. Поэтому предельные вероятности состояний СМО следует искать только в том случае, если ρ<1.

Как следует из первого уравнения системы (10), предельные вероятности СМО, представленной на рис.3, определяются соотношениями

(в скобках стоит сумма бесконечной геометрической прогрессии со знаменателем ρ). Если ρ<1, то эта сумма равна

.

Таким образом, предельная вероятность состояния S₀ СМО определяется соотношением .

Предельная вероятность любого состояния S_k СМО вычисляется по формуле (см. систему (10)):

. (11)

Т.к. ρ<1, то из последнего равенства следует, что вероятность p₀ наибольшая.

Рассмотрим среднее число заявок, находящихся на обслуживании , среднее число заявок в очереди и среднее число заявок в системе . При этом выполняется соотношение

.

Среднее число заявок на обслуживании находят как среднее арифметическое взвешенное от двух состояний: канал свободен и каналом обслуживается одна заявка, т.е.

.

Сомножители 0 и 1 в этой системе означают, что в системе на обслуживании находятся ноль заявок, когда канал свободен, или одна заявка, когда канал занят. Вероятности того, что канал свободен или занят соответственно равны p₀ и 1- p₀. Следовательно

. (12)

Среднее число заявок в системе также определяется по формуле взвешенного арифметического среднего:

.

Сумма называется бесконечной арифметико-геометрической прогрессией и вычисляется по формуле:

.

Таким образом получим

. (13)

Среднее число заявок в очереди найдем как разность двух предыдущих величин:

. 14)

Среднее время нахождения системы в том или ином состоянии равно среднему числу заявок, деленному на интенсивность потока заявок:

Пример. В универмаге имеется одна касса. Интенсивность потока покупателей составляет 0,9 покупателей в минуту. Интенсивность обслуживания покупателей кассой – один покупатель в минуту. Предполагается, что очередь может быть неограниченной длины. Определить показатели эффективности работы кассы и вероятность того, что ожидает своей очереди не более трех покупателей.

Решение. Найдем предельную интенсивность потока заявок:

Т.к. ρ<1, то очередь не может бесконечно возрастать и предельные вероятности существуют.

Предельная вероятность того, что у кассы нет ни одного покупателя

Соответственно вероятность того, что касса занята,

Среднее число заявок на обслуживании, в системе, в очереди найдем по приведенным выше формулам (12-14).

заявок,

заявок,

заявок.

Среднее время нахождения системы в том или ином состоянии будет равно:

мин.;

мин.;

мин.

Вероятность того, что у кассы ожидают не более трех покупателей, складывается из предельных вероятностей того, что у кассы нет покупателей или ожидает один, либо два, либо три покупателя, т.е.

.

Рассчитав предельные вероятности по вышеприведенной формуле, получим:

.

Упражнения

1. На телефонную линию приходит простейший поток вызовов с интенсивностью 0,9 выз./мин.; производительность линии 0,7 выз./мин. Вызов, пришедший на линию во время ее занятости, не обслуживается. Найти абсолютную пропускную способность линии, среднее время обслуживания од