Экономические приложения дифференциальных уравнений второго порядка
Пример 12.31.
Рассмотрим модель рынка с прогнозируемыми ценами. В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят и от тенеденции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены P(t).
Пусть функция спроса D и предложение S имеют следующие зависимости от цены P и ее производных: D(t) = 3P'' - P' – 2P +18,
S(t) = 4P'' + P' + 3P + 3.
Требуется установить зависимость цены от времени. Поскольку равновесное состояние рынка характеризуется равенством D = S, приравниваем правые части уравнений, откуда получим Р'' + 2Р' + 5Р = 15.
Последнее соотношение представляет собой линейное неоднородное дифференциальное уравнение второго порядка относительно функции Р(t).
Найдем общее уравнение однородного уравнения Р'' + 2Р' + 5Р = 0.
Характеристическое уравнение имеет вид λ2 + 2λ + 5 = 0. Его корни – комплексно-сопряженные числа: λ 1,2 = -1+2i.
Общее решение однородного уравнения Роо(t) = e-1 (C1 cos2t + C2 sin2t), где С1 и С2 – произвольные постоянные.
Частным решением возьмем Р = Рst – постоянную величину, которая представляет собой установившуюся цену. Подстановка в уравнение Р'' + 2Р' + 5Р = 15 частного решения дает значение Рst = 3.
Таким образом, общее решение неоднородного уравнения имеет вид Рон(t)= =3+ e-1(C1 cos2t +C2 sin2t).
Нетрудно видеть, что Рон(t) → Рst = 3 при t → ∞, то есть все интегральные кривые имеют горизонтальную асимптоту Р = 3 и колеблются около нее. Это означает, что все цены стремятся к установившейся цене Рst с колебаниями около нее, причем амплитуда этих колебаний затухает со временем.
Рассмотрим два частных решения
1) Задача Коши.
Пусть в начальный момент времени t = 0 известна цена, а также тенденция ее изменения, то есть Р = 4; Р′ = 1.
Подставляя первое условие в формулу Рон(t) = 3 + е-t(C1 cos2t + C2 sin2t), получим Р(0) = С1 + 3 = 4, откуда С1 = 1.
Таким образом, имеем Р(t) = 3 + е-t(cos2t +С2 sin2t).
Дифференцируя, получим Р′(t) = 3 + е-t[(2C2 – 1)cos2t + (C2 + 2)sin2t].
Подставляя t = 0 и используя второе условие задачи Коши, получим Р′(0) = 2С2 – 1 = 1, откуда С2 = 1.
Окончательно получим решение задачи Коши Р(t) = 3 + е-t(cos2t + sin2t).
2) Смешанная задача.
Пусть в начальный момент времени t =0 известны цена Р = 4 и спрос D = 16.
Поскольку первое начальное условие такое же, как и в случае 1), то имеем аналогичное решение Р(t) = 3 + е-t(cos2t +С2 sin2t).
Тогда производные функции Р(t) выражаются формулами
Р′(t) = е-t[(2C2 – 1)cos2t + (C2 + 2)sin2t], Р′′(t) = - е-t[(4C2 + 3)cos2t+(3C2 - 5)sin2t].
Следовательно Р′(0) = 2C2 – 1 и Р′′(0) = -4C2 - 3.
Имеем D(0)= 3P′′(0)-P′(0) – 2P(0) + 18 = 3(-4C2 – 3) – (2C2 – 1) - 2∙4 + 18 = 4, откуда C2 = -1.
Таким образом, решение смешанной задачи имеет вид
Р(t) = 3 + е-t(cos2t - sin2t).
Приложение 1
Формулы элементарной математики
1. Тождества сокращенного умножения
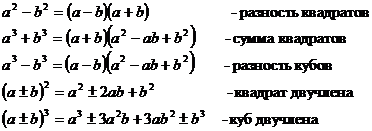
2. Квадратное уравнение ax2+bx+c=0, a ≠ 0
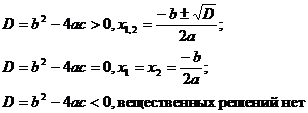
Теорема Виета:
Если D ≥ 0, то 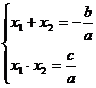
3. Разложение квадратного трехчлена на множители
Если D=b2-4ac ≥ 0, то ax2+bx+c=a(x-x1)(x-x2)
4. Степени
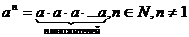 ;
;
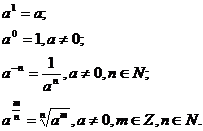
Свойства степеней:
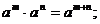
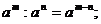
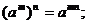
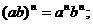
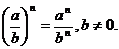
5. Логарифмы и их свойства
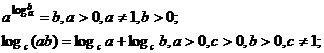
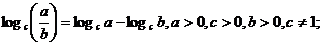
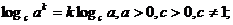
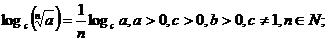
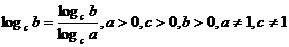 .
.
6. Тригонометрия
а) Знаки тригонометрических функций
| Четверть | функция | |||
| sinα | cosα | tgα | ctgα | |
| I | + | + | + | + |
| II | + | - | - | - |
| III | - | - | + | + |
| IV | - | + | - | - |
б) Значения тригонометрических функций при некоторых значениях
аргумента.
| Функция | Аргумент | |||||||
| (0о) | 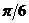 (30о) (30о) | 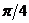 (45о) (45о) | 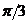 (60о) (60о) | 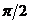 (90о) (90о) | 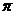 (180о) (180о) | 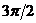 (270о) (270о) | 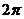 (360о) (360о) | |
| sinα | 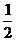 | 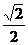 | 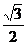 | -1 | ||||
| cosα | 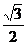 | 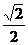 | 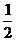 | -1 | ||||
| tgα | 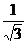 | 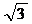 | - | - | ||||
| ctgα | - | 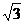 | 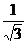 | - | - |
в) Формулы приведения.
| Функция | Аргумент | |||||||
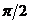 -α -α | 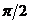 +α +α | 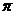 - α - α | 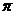 +α +α | 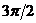 -α -α | 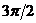 +α +α | 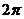 -α -α | 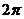 +α +α | |
| sinα | cosα | cosα | sinα | -sinα | -cosα | -cosα | -sinα | sinα |
| cosα | sinα | -sinα | -cosα | -cosα | -sinα | sinα | cosα | cosα |
| tgα | ctgα | -ctgα | -tgα | tgα | ctgα | -ctgα | -tgα | tgα |
| ctgα | tgα | -tgα | -ctgα | ctgα | tgα | -tgα | -ctgα | ctgα |
г) Зависимости между тригонометрическими функциями одного и того
же аргумента.
tgα= 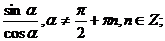
сtga= 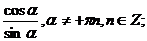
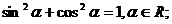
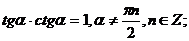
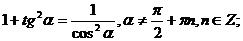
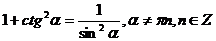 .
.
д) Формулы сложения для тригонометрических функций.
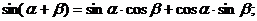
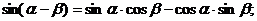
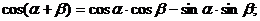
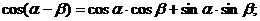
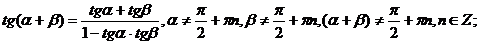
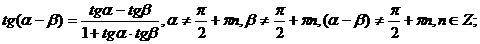
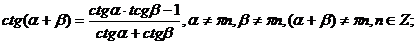
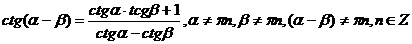 .
.
е) Тригонометрические функции двойного и тройного аргумента.
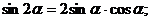
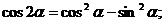
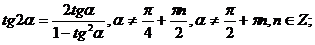
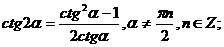
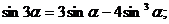
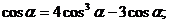
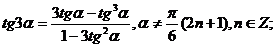
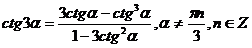 .
.
ж) Формулы половинного аргумента.
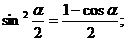
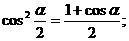
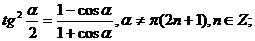
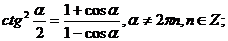
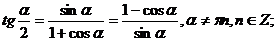
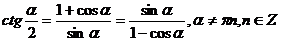 .
.
з) Формулы преобразования суммы и разности тригонометрических
функций в произведение.
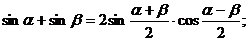
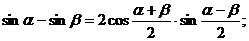
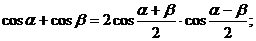
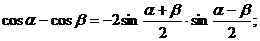
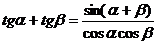
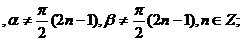
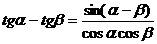
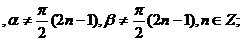
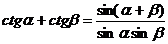
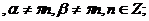
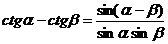
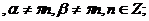
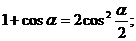
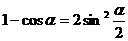 .
.
и) Формулы преобразования произведения тригонометрических функций в сумму.
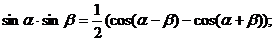
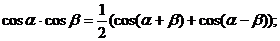
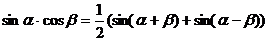 .
.
к) Простейшие тригонометрические уравнения.
| Уравнение | Формула решения | Частные случаи | Примечание |
| sinx=a | 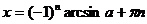 | 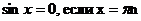 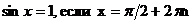 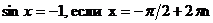 | 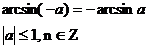 |
| cosx=a | 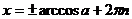 | 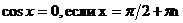 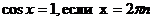 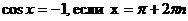 | 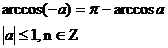 |
| tgx=a | 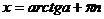 | 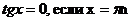 | 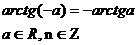 |
| ctgx=a | 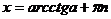 | 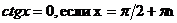 | 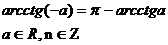 |
Приложение 2
Основные элементарные функции: свойства и графики
1. Степенные функции
1.1. f(x) = x2.
a) D(f) = /R;
б) E(f) = [0, +∞);
в) точка пересечения с осями координат – (0; 0);
г) функция четная (f(-x) = f(x));
д) функция непериодичная;
|
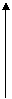 е) график функции:
е) график функции: 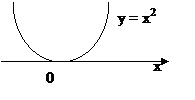 |
1.2. f(x) =  .
.
а) D(f) = /R 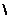 {0};
{0};
б) E(f) = /R 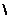 {0};
{0};
в) точек пересечения с осями координат нет;
г) функция нечетная (f(-x) = f(x));
д) функция непериодичная;
|
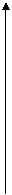 е) график функции:
е) график функции: 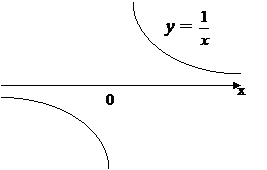 |
2. Показательная функция
f(x) = ах, а  (0, +∞)
(0, +∞) 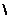 {1}.
{1}.
а) D (f) = /R;
б) E(f) = (0, +∞);
в) точка пересечения с осью Оу – (0; 1);
г) функция ни четная, ни нечетная;
д) функция непериодическая;
е) график функции:
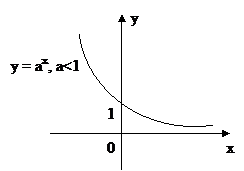 | |||
 |
3. Логарифмическая функция
f(x) = logax, a  (0, +∞)
(0, +∞) 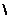 {1}.
{1}.
а) D (f) = (0, +∞);
б) E(f) = /R;
в) точка пересечения с осью Ох – (1; 0);
г) функция ни четная, ни нечетная;
д) функция непериодическая;
е) график функции:
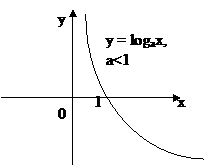 | |||
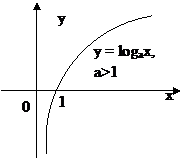 |
4. Тригонометрические функции
4.1. f(x) = sinx.
а) D (f) = /R;
б) E(f) =[-1; 1];
 в) точки пересечения с осью Ох – (
в) точки пересечения с осью Ох – ( 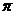 k; 0), k
k; 0), k  Z;
Z;
г) функция нечетная (f(-x) = -f(x));
д) функция периодическая с периодом Т = 2 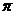 ;
;
е) график функции:

4.2. f(x) = cosx.
а) D (f) =/R;
б) E(f) =[-1; 1];
в) точки пересечения с осью Ох – ( 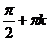 ; 0), k
; 0), k  Z, точка пересечения с осью Оу – (0; 1);
Z, точка пересечения с осью Оу – (0; 1);
г) функция четная (f(-x) = f(x));
д) функция периодическая с периодом Т = 2 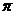 ;
;
 е) график функции:
е) график функции:
 |
4.3. f(x) = tgx.
а) D (f) =/R 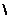 {
{ 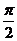 +
+ 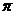 k}, k
k}, k  Z;
Z;
б) E(f) =/R;
в) точки пересечения с осью Ох – ( 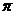 k; 0), k
k; 0), k  Z;
Z;
| |
 д) функция периодическая с периодом Т =
д) функция периодическая с периодом Т = 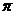 ;
;

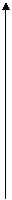

|
 |
4.4. f(x) = сtgx.
а) D (f) =/R 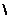 {
{ 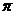 k}, k
k}, k  Z;
Z;
б) E(f) =/R;
в) точки пересечения с осью Ох – ( 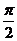 +
+ 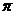 k; 0), k
k; 0), k  Z;
Z;
г) функция нечетная (f(-x) =- f(x));
д) функция периодичная с периодом Т = 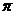 ;
;
е) график функции:
 |
5. Обратные тригонометрические функции
5.1. f(x) =arcsinx.
а) D (f) =[-1; 1];
б) E(f) =[- 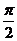 ;
; 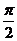 ];
];
в) точка пересечения с осями координат – (0; 0);
г) функция нечетная (f(-x) =- f(x));
д) функция непериодичная;
|
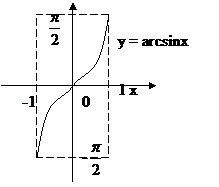 |
5.2. f(x) =arccosx.
а) D (f) =[-1; 1];
б) E(f) =[0; 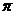 ];
];
в) точка пересечения с осью Оу – (0; 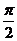 );
);
г) функция ни четная, ни нечетная;
д) функция непериодичная;
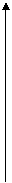
|
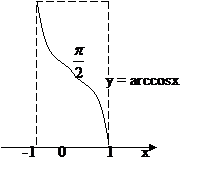 |
5.3. f(x) =arctgx.
а) D (f) =/R;
б) E(f) =[- 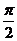 ;
; 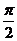 ];
];
в) точка пересечения с осями координат – (0; 0);
г) функция нечетная (f(-x) =- f(x));
д) функция непериодичная;
|

5.4. f(x) =arcctgx.
а) D (f) =/R;
б) E(f) =[0; 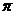 ];
];
в) точка пересечения с осью Оу – (0; 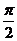 );
);
г) функция ни четная, ни нечетная;
д) функция непериодичная;
|
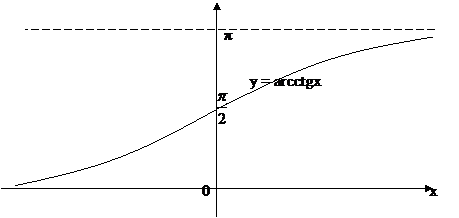
Литература
1. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. М.: Дело. 2002.
2. Высшая математика для экономистов. / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ. 2004.
3. Шипачев В.С. Высшая математика. М.: Высшая школа. 2003.
4. Васильев А.Б., Свешников А.Г., Тихонов А.Н. Дифференциальные уравнения. М.: Наука. 1978.
5. Смирнова Е.Л. Дифференциальное исчисление функций одной переменной. СПб.: ВИКА им. А.Ф. Можайского. 1993.
Оглавление
Предисловие........................................................................................... 3
Глава I.Введение в анализ.
1.1. Множества. Основные определения............................................... 4
1.2. Операции над множествами........................................................... 6
1.3. Функция одной переменной. Основные определения................... 7
1.4. Свойства функции........................................................................... 9
1.5. Способы задания функции............................................................. 9
1.6. Элементарные функции.................................................................. 10
Глава II.Предел и непрерывность функции одной переменной.
2.1. Последовательность и ее предел.................................................... 12
2.2. Предел функции в точке. Односторонние пределы...................... 13
2.3. Предел функции при х→ ∞. Бесконечно малые и бесконечно
большие функции................................................................................... 15
2.4. Основные теоремы о функциях, имеющих конечные пределы..... 17
2.5. Замечательные пределы.................................................................. 18
2.6. Сравнение функций......................................................................... 19
2.7. Асимптоты кривой.......................................................................... 22
2.8. Непрерывность функции в точке. Односторонняя непрерывность 24
2.9. Непрерывность функции на промежутке. Точки разрыва функции
и их классификация................................................................................ 26
Глава III.Производная и дифференциал функции одной переменной.
3.1. Производная функции в точке. Односторонние производные..... 30
3.2. Геометрический смысл производной............................................. 32
3.3. Понятие бесконечной производной............................................... 33
3.4. Основные правила дифференцирования функций........................ 34
3.5. Таблица производных основных элементарных функций............ 35
3.6. Дифференциал функции.................................................................. 37
3.7. Дифференцирование параметрически заданной функции............ 38
3.8. Производные и дифференциалы высших порядков...................... 38
Глава IV.Аналитические и геометрические приложения производных.
4.1. Основные теоремы дифференциального исчисления.................... 41
4.2. Правило Лопиталя.......................................................................... 42
4.3. Формула Тейлора........................................................................... 44
4.4. Возрастание и убывание функции.................................................. 44
4.5. Экстремумы функции..................................................................... 45
4.6. Направление выпуклости кривой................................................... 47
4.7. Точки перегиба кривой................................................................... 49
4.8. Построение графика функции........................................................ 51
Глава V.Функции нескольких переменных.
5.1. Понятие n-мерного координатного пространства........................ 54
5.2. Определение функции нескольких переменных............................ 55
5.3. Частные производные функции...................................................... 57
5.4.Геометрический смысл частных производных функции двух
переменных............................................................................................ 58
5.5 Дифференциал функции двух переменных..................................... 59
5.6. Частные производные высших порядков функции двух
переменных............................................................................................ 61
5.7. Экстремумы функции..................................................................... 62
Глава VI.Неопределенный интеграл.
6.1. Первообразная и неопределённый интеграл................................. 64
6.2. Основные свойства неопределенного интеграла........................... 64
6.3.Таблица основных неопределённых интегралов............................ 65
6.4. Основные методы интегрирования................................................ 66
6.5. Интегрирование простейших функций, содержащих
квадратный трехчлен............................................................................. 69
6.6. Интегрирование рациональных дробей........................................ 71
6.7. Интегрирование некоторых тригонометрических функций........ 75
6.8. Интегрирование некоторых иррациональных функций............... 78
Глава VII.Определенный интеграл.
7.1. Понятие определённого интеграла. Геометрический и
экономический смысл определённого интеграла................................. 82
7.2. Свойства определённого интеграла............................................... 85
7.3. Основные методы вычисления определённого интеграла........... 86
Глава VIII.Геометрические приложения определенного интеграла.
8.1. Вычисление площади плоской фигуры......................................... 88
|
8.3. Вычисление длины дуги плоской кривой...................................... 91
Глава IX.Несобственные интегралы.
9.1. Несобственные интегралы I рода (по бесконечному промежутку) 94
9.2. Свойства несобственных интегралов I рода.................................. 95
9.3. Признаки сходимости несобственных интегралов I рода............. 96
9.4. Несобственные интегралы II рода (от неограниченных функций)........ 97
Глава Х.Числовые ряды.
10.1. Основные определения и примеры.............................................. 100
10.2. Необходимый признак сходимости числового ряда. Операции
над числовыми рядами.......................................................................... 101
10.3. Знакоположительные ряды.......................................................... 102
10.4. Знакочередующиеся ряды............................................................ 107
10.5. Знакопеременные ряды................................................................. 108
Глава XI.Функциональные ряды.
11.1. Основные определения и примеры.............................................. 111
11.2. Степенные ряды. Свойства степенных рядов.............................. 113
11.3. Ряды Тейлора и Маклорена. Разложение функций в ряд
Тейлора и Маклорена............................................................................ 115
Глава XII.Обыкновенные дифференциальные уравнения.
12.1. Основные понятия и определения................................................ 119
12.2. Дифференциальные уравнения первого порядка. Классификация
решений.................................................................................................. 119
12.3. Дифференциальные уравнения первого порядка в нормальной и
диффернциальной форме....................................................................... 122
12.3.1. Уравнения с разделяющимися переменными........................... 122
12.3.2. Однородные дифференциальные уравнения и приводящиеся
к ним....................................................................................................... 124
12.3.3. Линейные уравнения первого порядка.Уравнение Бернулли. 127
12.3.4. Уравнения в полных диффернциалах. Интегрирующий множи-
тель......................................................................................................... 130
12.4. Дифференциальные уравнения второго порядка........................ 134
12.4.1.Основные понятия и определения. Задача Коши...................... 134
12.4.2. Уравнения, допускающие понижение порядка......................... 136
12.5. Линейные уравнения второго порядка........................................ 138
12.5.1. Основные понятия и определения............................................. 138
12.5.2. Линейные уравнения второго порядка с постоянными коэффици-
ентами..................................................................................................... 141
12.6. Экономические приложения дифференциальных уравнений второ-
го порядка.............................................................................................. 146
Приложение 1......................................................................................... 148
Приложение 2......................................................................................... 153
Литература............................................................................................. 159
