Интегрирование некоторых тригонометрических функций

1) Интегралы вида

Интеграл всегда сводится к интегралу от рациональной дроби с помощью подстановки .

Тогда .

Особенно удобно ею пользоваться, если под интегралом стоит дробь, в числителе и знаменателе которой стоят многочлены относительно sinx и cosx степени не более первой.

Пример 6.20.

Найдем интеграл .

Сделаем подстановку .

.

Заметим, что подстановка приводит иной раз к сложным выкладкам. Ниже указаны случаи, когда цель может быть достигнута с помощью более простых подстановок.

2) Интегралы вида .

Если имеет место тождество , то удобнее сделать подстановку .

Тогда .

Пример 6.21.

Найдем интеграл .

Так как ,

то делаем подстановку , тогда

, , .

.

3) Интегралы вида ,

Для нахождения этих интегралов применяется подстановка sinx = t (cosxdx = dt) и cosx = t (-sinxdx = dt) соответственно.

Пример 6.22.

Найдем интеграл .

Сделаем подстановку:

.

4) Интегралы вида , m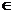, n /N.

Интеграл берётся понижением степени с помощью формул: .

Пример 6.23.

Найдем интеграл .

.

5) Интегралы вида .

Хотя бы одно из чисел – целое положительное и нечетное. Например, .

Имеем .

Дальше можно сделать подстановку: .

Пример 6.24.

Найдем интеграл I = .

Интегралы вида

Подынтегральные выражения преобразуются в сумму тригонометрических функций с помощью формул:

Пример 6.25.

Найдем интеграл .

Интегрирование некоторых иррациональных функций

Основной приём интегрирования таких функций заключается в рационализации подынтегрального выражения.

1) Интегралы вида .

Интеграл берется с помощью подстановки , где – наименьший общий знаменатель дробей , i = .

Пример 6.26.

Найдем интеграл .

Дан интеграл где N = 4. Сделаем подстановку: .

.

2) Интегралы вида .

Интегралы рационализуются с помощью соответствующих тригонометрических подстановок:

– подстановка: ;

– подстановка: ;

– подстановка: .

Пример 6.27.

Найдем интеграл .

Сделаем подстановку: .

,

=

=

.

Интегрирование дифференциальных биномов.

Дифференциальным биномом называется выражение .

Интегралы вида берутся в элементарных функциях только в следующих трёх случаях:

а) – целое;

б) – целое.

В этом случае делается подстановка: , где ;

в) – целое.

Подстановка: .

Пример 6.28.

Найдем интеграл .

.

Здесь , поэтому имеет место второй случай. Подстановка: , .

Пример 6.29.

Найдем интеграл .

.

Здесь m = 0, n = 4, p = – , , поэтому имеем третий случай.

Подстановка: ,

=

=

=

4) Интегралы вида .

Интегралы берутся с помощью подстановок Эйлера.

а) Если , то применяется первая подстановка Эйлера: ;

б) Если , то делается вторая подстановка Эйлера: ;

в) Если имеет различные двещественные корни x₁ и x₂, то применяется третья подстановка Эйлера: .

Пример 6.30.

Найдем интеграл .

Так как , то применим первую подстановку Эйлера:

, .

– .

Глава VII. Определенный интеграл

Понятие определённого интеграла. Геометрический и экономический смысл определённого интеграла

Определение 7.1.

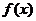Пусть функция определена и ограничена на отрезке [a, b] и – произвольное разбиение этого отрезка на частей (рис. 7.1).

Сумма вида , где называется интегральной суммой функции 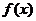на отрезке [a, b].

рис. 7.1.

Определение 7.2.

Диаметром разбиения называется наибольшая длина частичного отрезка разбиения, то есть .

Определение 7.3.

Если существует конечный предел суммы при условии, что диаметр разбиения , не зависящий от способа разбиения отрезка интегрирования [a,b], а также от способа выбора точек , то этот предел называется определённым интегралом функции f(x) на отрезке [a, b] ( в пределах от 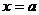до ).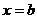

Обозначение: .

В этом случае функция у=f(х) называется интегрируемой на отрезке [a, b] (по Риману), выражение называется подынтегральным выражением, функция 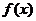– подынтегральной функцией, числа a, b называются нижним и верхним пределами интегрирования соответственно.

Теорема 7.1.(о достаточных условиях интегрируемости)

Непрерывные и кусочно-непрерывные отрезки на [a, b] функции являются интегрируемыми.

Геометрический смысл интеграла.

Геометрически определённый интеграл является алгебраической суммой площадей фигур, составляющих так называемую криволинейную трапецию , ограниченную указанной кривой , прямыми x=a, x=b и осью Ох (рис.7.1). Причем, площади частей, расположенных выше оси 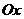берутся со знаком «+», а площади частей, расположенных ниже оси 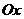– со знаком «–».