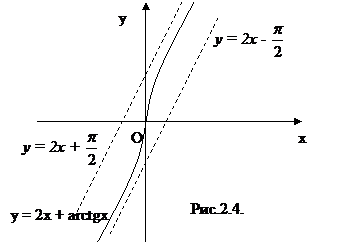Основные теоремы о функциях, имеющих конечные пределы

Теорема 2.3. (о единственности предела функции)

Пусть функция f(x) имеет конечный предел в точке 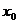, тогда такой предел единственный.

Теорема 2.4. (о связи функции, имеющей конечный предел, с бесконечно малой функцией).

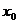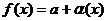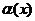Для того, чтобы функция f(x) имела конечный предел а в точке необходимо и достаточно, чтобы она была представлена в виде , где - бесконечно малая функция при .

Теорема 2.5. (об арифметических свойствах пределов).

Пусть функции f(x) и g(x) имеют в точке 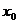конечные пределы, тогда:

1) 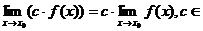/R;

2) ;

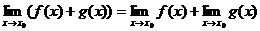3) ;

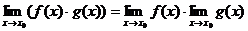4) .

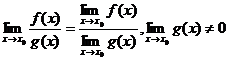Пример 2.8.

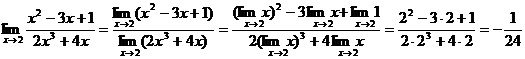
Теорема 2.6. (о замене переменной при вычислении предела).

Если 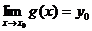, то 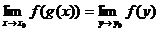при условии, что предел в правой части последнего равенства существует.

Замечательные пределы

Теорема 2.7. (о первом замечательном пределе).

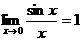(х выражено в радианах).

Следствия

1.

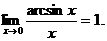
2.

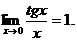
3.

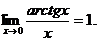
Пример 2.9.

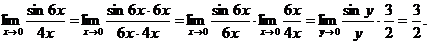, где у = 6х (здесь используется теорема 2.5 о замене переменной при вычислении предела).

Пример 2.10.

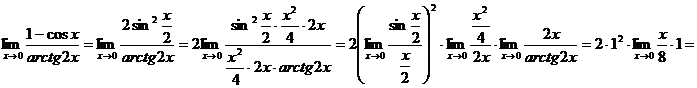
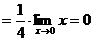
Замечание 2.6. (о числе е).

Рассмотрим последовательность 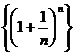. Можно показать, что такая последовательность имеет конечный предел, который обозначается е, то есть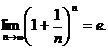

е является иррациональным числом, вычисленным приближенно: .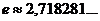

Показательная функция 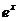называется экспоненциональной функцией или экспонентой.

Логарифм положительного числа х, вычисленный по основанию е, называется натуральным логарифмом и обозначается ln x.

Экспонента и натуральный логарифм играют важную роль в математическом анализе и его приложениях.

Теорема 2.8. (о втором замечательном пределе).

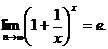
Следствия

1.

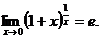
2.

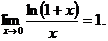
3.

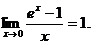
4. 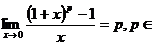/R.

Пример 2.11.

.

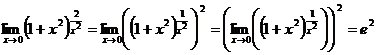Пример 2.12.

.

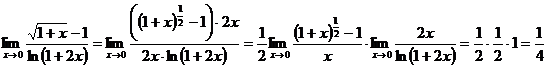Сравнение функций

Определение 2.11.

Пусть функции f(x) и g(x) определены в некоторой окрестности точки х 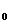за исключением возможно самой точки х .

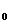1. Если 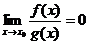, то говорят, что функция f(x) мала по сравнению с функцией g(x) при .

Обозначение: f(x) = о (g(x)), .

2. Если 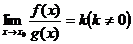, то говорят, что функции f(x) и g(x) одного порядка при .

Обозначение: f(x) = О (g(x)), .

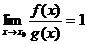3. Если, в частности, , то функции f(x) и g(x)называют эквивалентными при .

Обозначение: f(x)~ g(x) при .

Пример 2.13.

Доказать, что многочлен эквивалентен своему старшему члену при 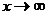, то есть 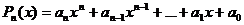~ 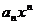при .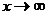

Решение

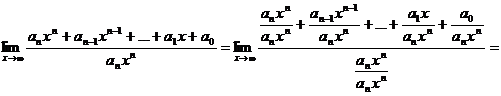
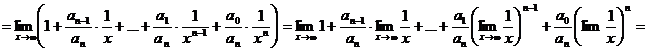
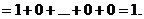
Таким образом, 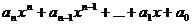~ 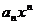при .

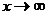Пример 2.14. (таблица эквивалентных бесконечно малых функций).

Используя замечательные пределы и следствия к ним, можно составить следующую таблицу:

sin x ~ x при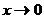

tg x ~ x при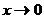

arcsin x ~ x при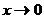

arctg x ~ x при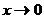

ln(1+x) ~ x при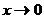

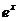-1 ~ x при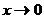

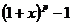~ px при .

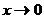Теорема 2.9. (о некоторых эквивалентных заменах).

1. Если f(x) ~ f₁(x) и g(x) ~ g₁(x) при , то при f(x)g(x) ~ f₁(x) g₁(x) и ~ .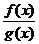

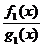2. Если f(x) = о (g(x)), при , то при f(x)+ g(x) ~ g(x).

3. Если f(x) ~ c₁ h(x) и g(x) ~ c₂h(x) при , то f(x) + g(x) ~ (с₁+ с₂)h(x) при условии, что с₁+ с₂ ≠ 0.

4. Если 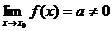, то f(x) ~ а при .

Теорема 2.10. (о замене на эквивалентную при вычислении предела отношения).

Пусть f(x) ~ f₁(x) и g(x) ~ g₁(x) при , тогда .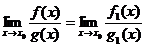

Замечание 2.7.

В том случае, когда 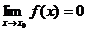и 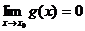, задача вычисления 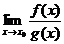называется задачей раскрытия неопределенности .

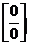Аналогично определяются неопределенности

С помощью теорем 2.9., 2.10. и таблицы эквивалентных бесконечно малых функций можно существенно упростить вычисление пределов, особенно в условиях неопределенности.

Пример 2.15.

Вычислить .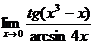

Решение

Поскольку 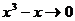, если 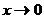, то из таблицы эквивалентных бесконечно малых функций имеем 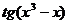~ 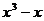при 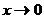. Аналогично arcsin 4x ~ 4x при 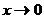. Заменяя числитель и знаменатель дроби под знаком предела эквивалентными функциями, получим

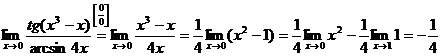
Пример 2.16.

Вычислить .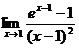

Решение

Если 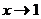, то х-1→0, а значит, можно воспользоваться таблицей эквивалентностей. Имеем 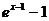~ х-1 при 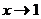, откуда .

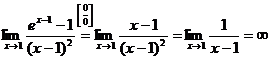Пример 2.17.

Вычислить .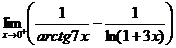

Решение

Имеем arctg 7x ~ 7x, ln(1+3x) ~ 3x при 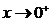, откуда 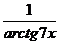~ ~ 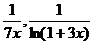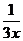при .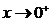

Согласно пункту 3 теоремы 2.8. 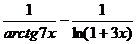~ 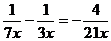при .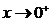

Таким образом, .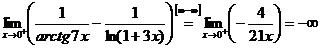

Асимптоты кривой

Определение 2.12.

Прямая х=х₀ называется вертикальной асимптотой кривой y=f(x), если хотя бы один из односторонних пределов 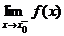, 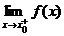равен +∞ или -∞.

Пример 2.18.

Найти вертикальные асимптоты кривой .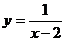

Решение

Будем искать односторонние пределы функции 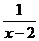в точке х₀ = 2, то есть в той точке, в которой эта функция не определена.

у

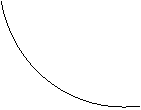Имеем 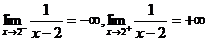, следовательно, х = 2 – вертикальная асимптота кривой .

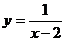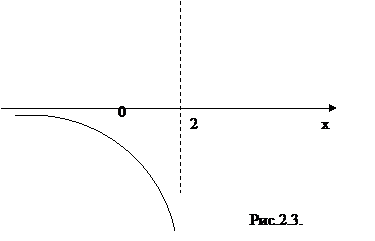
Как видно из рис.2.3., график исходной функции неограниченно приближается к вертикальной асимптоте х = 2 при х→2.

Определение 2.13.

Прямая y = kx + b называется наклонной асимптотой кривой y = f(x) при 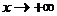, если f(x) = kx + b+ 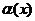, где 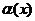- бесконечно малая функция при .

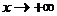Аналогично определяется наклонная асимптота кривой y = f(x) при .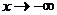

Теорема 2.11. (о наклонных асимптотах кривой).

1. Для того, чтобы прямая y = kx + b являлась асимптотой кривой y = f(x) при 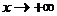, необходимо и достаточно, чтобы одновременно выполнялись условия .

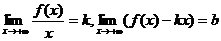2. Для того, чтобы прямая y = kx + b являлась асимптотой кривой y = f(x) при 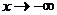, необходимо и достаточно, чтобы одновременно выполнялись условия .

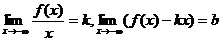Пример 2.19.

Найти наклонные асимптоты кривой y = 2x + arctg x.

Решение

1. Пусть .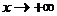

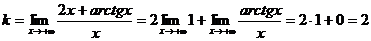(второй предел равен нулю,

поскольку arctg x ~ 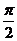при x→+∞), 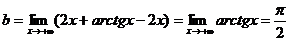. Таким образом, прямая y = 2x + 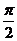является наклонной асимптотой исходной кривой при x→+ ∞.

2. Теперь рассмотрим x→- ∞.

,

.

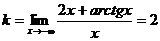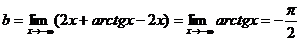Следовательно, прямая y = 2x - 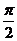является наклонной асимптотой исходной кривой при x→- ∞ (рис.2.4).