Тема 3. решение систем линейных уравнений
3.1. Метод обратной матрицы
Пример. Решить систему уравнений: 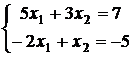 .
.
1. Запишем систему в матричном виде: вместо 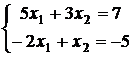 имеем
имеем 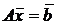 , где
, где 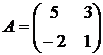 ;
; 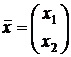 ;
; 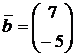 , то
, то 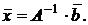
2. Найдем обратную матрицу:
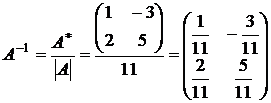 .
.
3. Вычисляем искомый вектор:
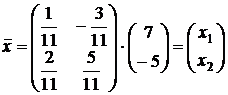 ,
,
где
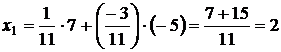 ,
,
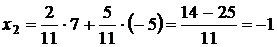 .
.
Сделаем проверку, подставив полученный результат в данную систему:
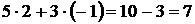 .
.
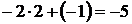 .
.
3.2. Метод Гаусса
Рассмотрим систему m уравнений,связывающих n неизвестных
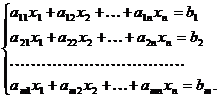 (1)
(1)
Здесь aij (1≤i≤m , 1≤j≤m) коэффициенты; bj – cвободные члены. Если все коэффициенты и свободный член какого- то уравнения равны нулю , то вычеркиваем его из системы. Если коэффициенты при всех неизвестных равны нулю, а b≠0 , то система решений не имеет .
Условимся,что первым в системе (1) стоит уравнение, в котором коэффициент при первом неизвестном отличен от нуля (например а11≠0). Запишем систему (1) в виде матрицы опустив неизвестные и отделяя свободные члены вертикальной чертой
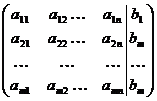 (2)
(2)
Делим все элементы первой строки на 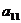
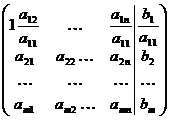 (3)
(3)
Затем из каждой 2-й,3-й,...,m-й строки матрицы (3) вычитаем почленно первую строку умноженной соответственно на a21,a31,..,am1 ; при этом результат вычитания получится в виде
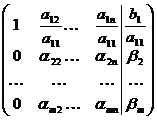 (4)
(4)
где 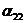 =
= 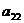 -
- 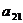
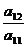 ,...,
,..., 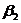 =b2 –
=b2 – 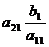 .
.
Повторяя указанную операцию необходимое число раз,получим матрицу вида
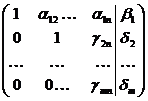 (5)
(5)
Полученной матрице соответствует система уравнений
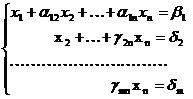 (6)
(6)
Пользуясь тем,что система имеет треугольный вид,ее можно решать последовательно, начиная с последнего уравнения.
Пример. Решить систему линейных уравнений методом Гаусса
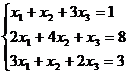 (7)
(7)
Матрица этой системы имеет вид

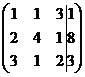 (8)
(8)
Первую строку матрицы (8) умноженную на 2 и на 3 вычитаем из второй и третьей, соответственно
( 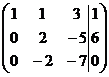 (9)
(9)
Далее, к третьей строке матрицы (9) прибавив вторую, получим матрицу
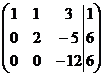
соответствующей системе
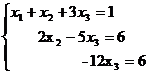
Значит, решением системы (7) будет
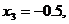
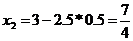 ,
, 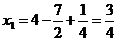 .
.
ТЕМА 4. ПРОИЗВЕДЕНИЕ ПРЕОБРАЗОВАНИЙ
Пусть даны линейные преобразования f и g соответственно с матрицами А и В в некотором базисе. Тогда произведение этих преобразований имеет матрицу ВА в том же базисе. Отметим, что в общем случае АВ ¹ ВА.
Например, преобразование g с матрицей 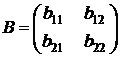 переводит точку М(х, у) в точку М¢(х¢, у¢) по формулам
переводит точку М(х, у) в точку М¢(х¢, у¢) по формулам
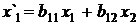
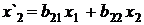 . (2)
. (2)
Преобразование А с матрицей 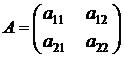 переводит точку М¢(х¢, у¢) в точку М²(Х2², У2²) по формулам
переводит точку М¢(х¢, у¢) в точку М²(Х2², У2²) по формулам
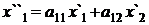 ,
, 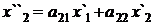 . (3)
. (3)
Чтобы получить формулы результирующего преобразования точки М в точку М², надо подставить в (3) выражения (2). Получим
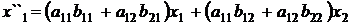 ,
,
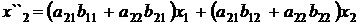 .
.
Стало быть, матрица произведения преобразований есть
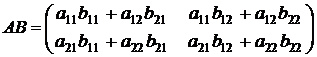 .
.
ТЕМА 5. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ
ПРЕОБРАЗОВАНИЙ
Пусть j- линейное преобразование, 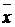 - вектор, отличный от нуля. Определение. Ненулевой вектор
- вектор, отличный от нуля. Определение. Ненулевой вектор 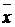 , удовлетворяющий равенству
, удовлетворяющий равенству
j 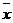 = l
= l 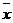 ,
,
где l -некоторое действительное число, называется собственным вектором преобразования j, число l - собственным значением этого преобразования.
Если А - матрица линейного преобразования, Х - матрица-столбец из координат вектора 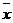 , то равенство (1) можно записать в матричном виде
, то равенство (1) можно записать в матричном виде
АХ = lХ.
Перенося члены в одну сторону получим
AX- 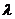 X=0 или (A-
X=0 или (A- 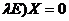
Уравнение 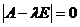 для собственных значений называется характеристическим
для собственных значений называется характеристическим
уравнением .
Пример
Пусть преобразование j имеет матрицу
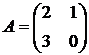 .
.
Найти собственные векторы матрицы.
Решение. Сначала найдем собственные значения матрицы. Характеристическое уравнение имеет вид
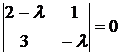 ,
,
или 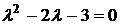 . Корнями этого уравнения являются l1 = -1,
. Корнями этого уравнения являются l1 = -1, 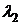 =3. Обозначаем через
=3. Обозначаем через 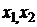 координаты собственного вектора
координаты собственного вектора 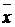 .
.
Тогда уравнение 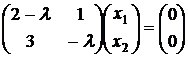 при l = l1 = -1 имеет вид
при l = l1 = -1 имеет вид
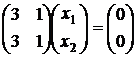 ,
,
или в раскрытом виде 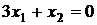 . Полагая
. Полагая 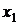 =a, найдем отсюда
=a, найдем отсюда 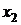 = -3a. Следовательно, собственные векторы, отвечающие корню l1, имеют вид
= -3a. Следовательно, собственные векторы, отвечающие корню l1, имеют вид 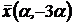 , где a - любое число, отличное от нуля.
, где a - любое число, отличное от нуля.
ТЕМА 6. КОМПЛЕКСНЫЕ ЧИСЛА
Комплексными называются числа вида z=x+iy, где x и y-действительные числа, а i2 =-1. Число x называется действительной частью комплексного числа z, а число y – коэффициент при i – мнимой частью. Число 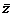 =x-iy называется сопряженным к числу z=x+iy. У сопряженных чисел равны действительные части, а мнимые отличаются только знаком. Числу z можно сопоставить вектор, направленный из начала O в точку z. Модуль
=x-iy называется сопряженным к числу z=x+iy. У сопряженных чисел равны действительные части, а мнимые отличаются только знаком. Числу z можно сопоставить вектор, направленный из начала O в точку z. Модуль 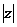 комплексного числа z вычисляется по формуле
комплексного числа z вычисляется по формуле
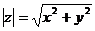 .
.
Угол 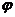 образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
Любое комплексное число z можно представить в алгебраической форме z = x + iy и в тригонометрической форме z= r (cosj +isinj). Здесь 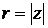 , j=Аrgz -, причем различные значения аргумента
, j=Аrgz -, причем различные значения аргумента 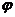 отличаются на 2
отличаются на 2 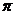 k
k  , где к - целое число. Под главным значением аргумента понимается значение j, удовлетворяющее условию -
, где к - целое число. Под главным значением аргумента понимается значение j, удовлетворяющее условию - 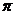 <j<
<j< 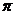 . Таким образом Аrgz = аrgz+2
. Таким образом Аrgz = аrgz+2 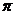 к.
к.
Комплексные числа z еще можно представить в показательной форме z =rеij, где r и j - то, что и в тригонометрической форме.
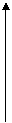 y
y
z
 |
r
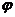
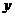
 o
o 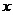 x
x
Рис.2
Пример
Найти корни уравнения 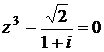 .
.
Решение. Находим модуль и аргумент числа 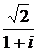
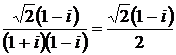
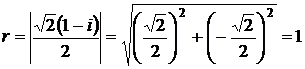
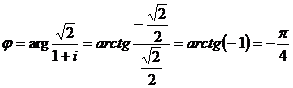 .
.
Тогда корни данного уравнения определяем по формулам
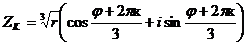 , к = 0,1,2, т.е. уравнение имеет три корня:
, к = 0,1,2, т.е. уравнение имеет три корня:
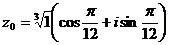 , при к=0;
, при к=0;
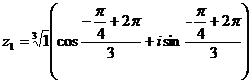 , при к=1;
, при к=1;
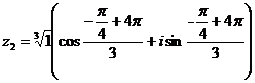 , при к=2
, при к=2
или 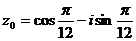
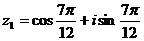
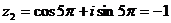
КОНТРОЛЬНАЯ РАБОТА № 1
Задание 1. Решить систему уравнений методом Гаусса и с помощью обратной матрицы
1. 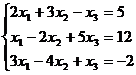
2. 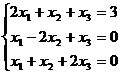
3. 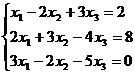
4. 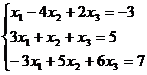
5. 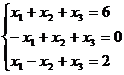
6. 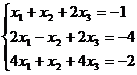
7. 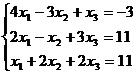
8. 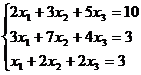
9. 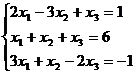
10. 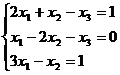
11. 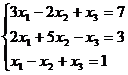
12. 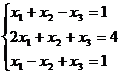
13. 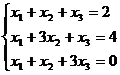
14. 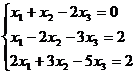
15. 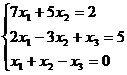
6. 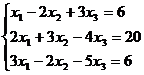
17. 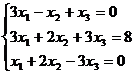
18. 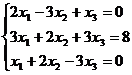
19. 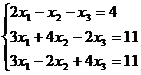
20. 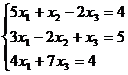
21. 
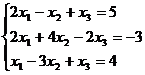
22. 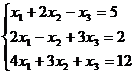
23. 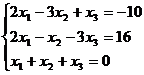
28. 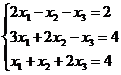
24. 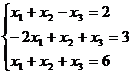
25. 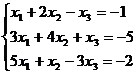
26. 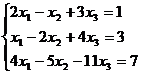
27. 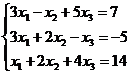

 29.
29. 
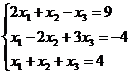
30. 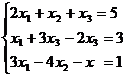

Задание 2.
В задачах 1-30 даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X"= 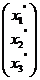 через X=
через X= 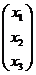
1. 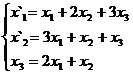
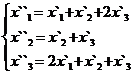
2. 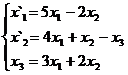
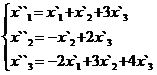
3. 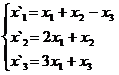
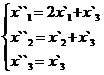
4. 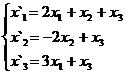
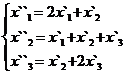
5. 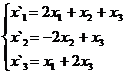
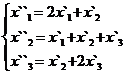
6. 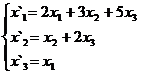
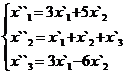
7. 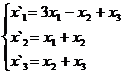
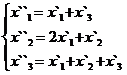
8. 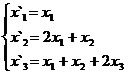
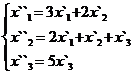
9. 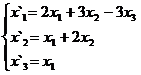
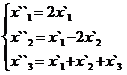
10. 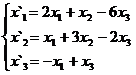
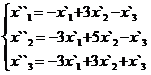
11. 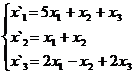
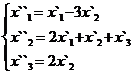
12. 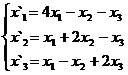
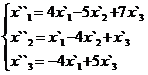
13. 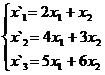
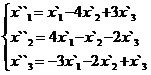
14. 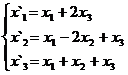
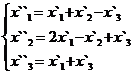
15. 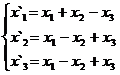
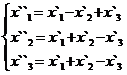
16. 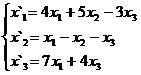
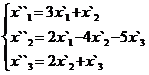
17. 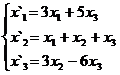
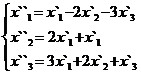
18. 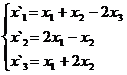
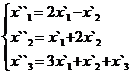
19. 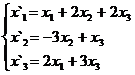
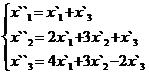
20. 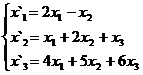
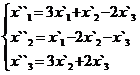
21. 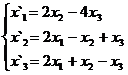
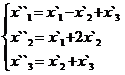
22. 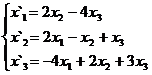
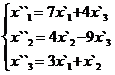
23. 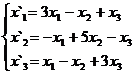
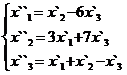
24. 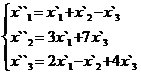
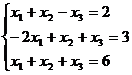
25. 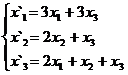
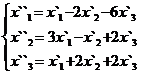
26. 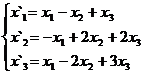
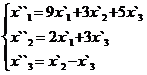
27. 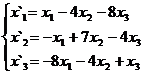
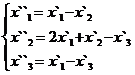
28. 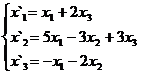
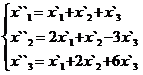
29. 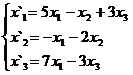
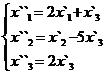
30. 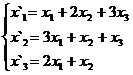
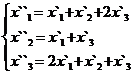
Задание 3.
Найти собственные векторы и собственные значения линейного преобразования, заданного в некотором базисе матрицей.
1. 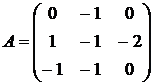 2.
2. 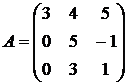 3.
3. 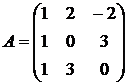
4. 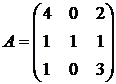 5.
5. 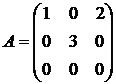 6.
6. 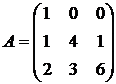
7. 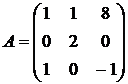 8.
8. 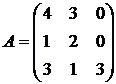 9.
9. 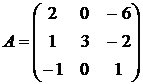
10.  11.
11. 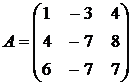 12.
12. 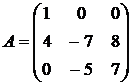
13. 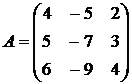 14.
14. 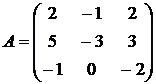 15.
15. 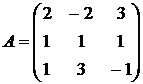
16. 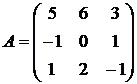 17.
17.  A=
A= 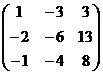 18.
18. 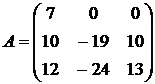
19. 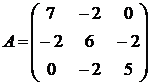 20.
20. 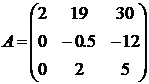 21.
21. 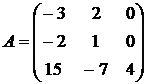
22. 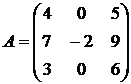 23.
23. 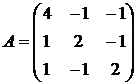 24.
24. 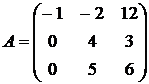
25. 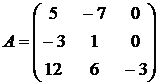 26.
26. 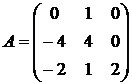 27.
27. 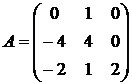
28. 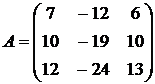 29.
29. 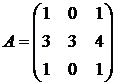 30.
30. 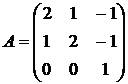
Задание 4.
Дано комплексное число 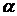 :
:
1) Записать число 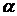 в алгебраической и тригонометрической формах.
в алгебраической и тригонометрической формах.
2) Найти и изобразить на плоскости все корни уравнения Z3 + 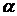 = 0.
= 0.
1. 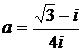 2.
2. 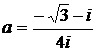 3.
3. 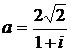 4.
4. 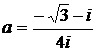
5. 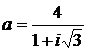 6.
6. 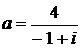 7.
7. 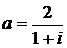 8.
8. 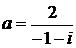
9. 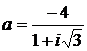 10.
10. 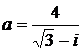 11.
11. 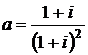 12.
12. 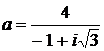
13. 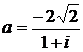 14.
14. 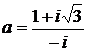 15.
15. 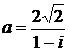 16.
16. 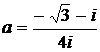
17. 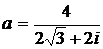 18.
18. 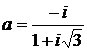 19.
19. 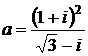 20.
20. 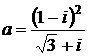
21. 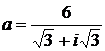 22.
22. 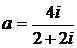 23.
23. 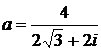 24.
24. 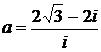
25. 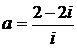 26.
26. 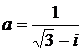 27.
27. 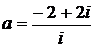 28.
28. 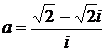
29. 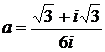 30.
30.