Предел функции в бесконечности и в точке.

Предел функции в бесконечности и в точке.

Число А называется пределом функции у=f(x) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 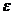>0, найдется такое положительное число S>0, чтодля всех х таких, что 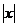>s, верно неравенство 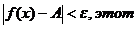предел функции обозначается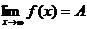

Число А называется пределом функции f(x) при х, стремящемся к 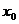(или в точке 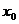), если для любого даже сколь угодно малого положительного числа 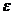>0, найдется такое положительное число 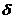>0, что для всех х, не равных 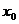и удовлет.условию 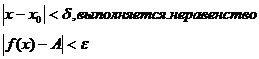,этот предел обозначается .

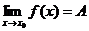Замечание 1. Определение предела не требует существования функции в самой точке .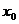

Непрерывность функции действительной переменной в точке и на отрезке. Свойства функций, непрерывных на отрезке.

Функция f(x) называется непрерывной в точке 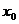,если она удовлетворяет след.трем условиям: 1)определена в точке 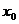(т.е. существует f( 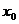)); 2) имеет конечный предел функции при 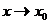;3) этот предел равен значению функции в точке 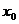,т.е.

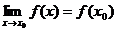
Функция y=f(x) называется непрерывной в точке 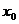,если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: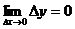

Св-ва функций, непрерывных на отрезке:

1) Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.

2) Если функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения М.

3) Если функция у=f(x) непрерывна на отрезке [a,b] и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка 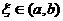такая, что f( 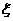)=0/

7. Производная функции и дифференциал.

Производной функции у=f(x) наз.предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю( если этот предел существует): .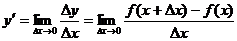

Нахождение производной функции наз. Дифференцированиемэтой функции. Если функция в точке х имеет конечную производную, то функция наз. Дифференцируемойв этой точке.

Если функция у=f(x) дифференцируема в точке 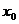, то она в этой точке непрерывна. (непрерывность функции-необходимое, но недостаточное условие дифференцируемости функции.)

Дифференциалом функцииназ.Главная, линейная относительно 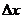часть приращения функции, равная 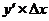. Dy=dx=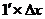

Dy= .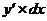

Дифференциал равен приращению ординаты касательной в данной точке, когда х получает приращение .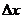

Св-ва дифференциала: 1)d(cf)=cdf, c=const. D(cf)=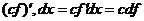

2)d(f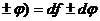

3)d(f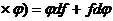

4)d(f/ .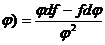

8. Производные и дифференциалы высших порядков.

Производной n-ого порядка наз.производная от производной (n-1)-ого порядка. Обозначение: 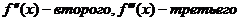и т.п. Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры.

Дифф.Высш.порядков.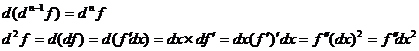

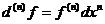
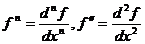
Формула Ньютона-Лейбница .

Теорема: Пусть функция у=f(x) непрерывна на отрезке [а,в] и F(x) – любая первообразная для f(x) на [а,в] .

Тогда определённый интеграл от функции f(x) на [а,в] равен приращению первообразной F(x) на этом отрезке, т.е.

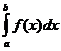= F(b) – F(a)

Алгоритм вычисления: 1. получить первозданную F(x) для подынтегральной ф-ии. f(x) с помощью нахождения неопределённого интеграла.

2. применить формулу (Вычисляя приращение первообразной равное искомому интегралу). Обозначение для приращения первообразной :F(x) = F(b) – F(a)

РАВНОМЕРНО СХОДЯЩИЙСЯ РЯД

функциональный ряд 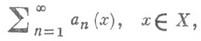(1)

Условие равномерной сходимости ряда (1) на множестве Xбез использования понятия суммы ряда дает Ноши критерий равномерной сходимости ряда. Достаточное условие равномерной сходимости ряда дается Вейерштрасса признаком.

т. е. если ряд (1) удовлетворяет условиям признака Веяорштрасса равномерной сходимости рядов. В силу этого признака правильно сходящийся на множестве Xряд равномерно сходится на этом множестве. Обратное, вообще говоря, неверно; однако во всяком равномерно сходящемся на множестве Xряде можно так объединить следующие друг за другом его члены в конечные группы, что получившийся при этом ряд будет уже правильно сходиться на множестве X.

Ряды Тейлора и Маклорена.

Ряд Маклорена:

Пусть f(x)- определенная и n-раз дифференцированная в окрестности точки х=0 функция, она может быть представлена ввиде степенного ряда( разложена в степенной ряд).

f(x)= 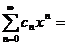C₀+C₁X+С₂Х²+...+С_nХⁿ

коэф-ты ряда:

f’(x)=C₁+2C₂X+3C₃X²+...+nC_nX^n-1

f“(x)=2C₂X+3∙2C₃X+...+n(n-1)C_nX^n-2

х=0,

f’(0)= C₁ => С₀=f(0)

f”(0)=2∙1 C₂=>C₁=f’(0)

f’”(0)=3∙2C₃ =>C₂=f”(0)/2!

f⁽ⁿ⁾(0)=n!C_n =>C_n=f⁽ⁿ⁾(0)/n!

Ряд Макларена: f(x)=f(0)+f’(0)∙x\1!+ f”(0)∙x²\2!+ f”’(0)∙x³\3!+..+ fⁿ(0)∙xⁿ\n!+..

Замечание1. Не всякая ф-ция может быть разложена в ряд Мак-на. Может получиться расх-ся ряд или ряд будет сводиться к др ряду.

Замечание2. Достаточное условие разложения ф-ции вряд Мак-на яв-ся ограниченность всех её производных в окрестности т.Х=0 одним и тем же числом, т.е. |f⁽ⁿ⁾(x)|≤C

*Если ф-ция раскладывается в ряд Маклорена, то это разложение единств-е.

Пр1: y=e^x

F(x)=1+x\1!+x²\2!+x³\3!+..+ xⁿ\n!+.. Отв:(-∞;+∞)

Пр2: f(x)=sinx

f’(x)=cosx, f’(0)=1

cos’x=-sinx, f”(0)=0

(-sinx)’=-cosx, f”’(0)=-1

(-cosx)’=sinx, f^IV(0)=0

Ряд: sinx=x- x³\3!+ x⁵\5!- x⁷\7!+..+(-1)ⁿx²ⁿ⁺¹\(2n+1)!+..

Ряд Тейлора:

Если ф-ция f(x) (n-1) раз дифференцируемых в окрестности т.Х₀, то для любого значения х из этой окрестности справедливы ф-ции Тейлора:

f(x)=f(x₀)+f’(x₀)(x-x₀)+f”(x₀)(x-x₀)²\2!+..+ fⁿ(x₀)(x-x₀)ⁿ\n!+Rn(x); Rn-остаточный член формулы Тейлора.

Rn= f⁽ⁿ⁺¹⁾(ξ)(x-x₀)ⁿ⁺¹\(n+1)!

Предел и непрерывность.

Число А-предел ф-ции Z=f(x,y) в т.М₀(х₀,у₀), если для любого сколь угодно малого положит числа 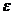>0, найдётся положит число ∂>0(зависящее от Е, ∂=∂(Е)), такое что для всех точек М (x,y), отстоящих от т.М₀(х₀,у₀) на расст ρ меньше, чем ∂ (0<ρ<∂) выполняется |f(x,y)-A|<E или lim(x→x₀, y→y₀)f(x,y)=A.

Ф-ция Z=f(x,y) непрерывна, если выполняется три усл:

1)она определена в этой т.(x₀, y₀)

2)сущ-ет конечный предел функции в т.М0.

3)этот предел=значению ф-ции lim(x→x₀, y→y₀)f(x,y)=f(x₀, y₀) в т.(x₀, y₀)

Обыкновенные дифференциальные уравнения. Основные понятия. Краевая задача и задача Коши.

Определение: Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных. Эти переменные и производные различных порядков данной функции. Если независимая переменная одна- обыкновенные Дифференциальные уравнения, если более - дифференциальные уравнения частных производных.

Решение дифференциального уравнения- такая функция у=у(х) , которая при подстановке ее в это уравнение образует его в тождество.

Порядок Дифференциального уравнения определяется порядком старшей производной.

Интеграл Дифференциального уравнения- решение полученное в неявной форме в виде G (x ; y)=0

Общее решение дифференциального уравнения У=Ф(х,с1,…..Еn)

Частное решение (при подстановке) Задачи:

1. Коши . Все дополнительные условия ставятся в одной точке

2. Краевая. Условия ставятся в разных точках ( как минимум два уравнения)

Предел функции в бесконечности и в точке.

Число А называется пределом функции у=f(x) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 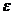>0, найдется такое положительное число S>0, чтодля всех х таких, что 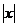>s, верно неравенство 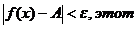предел функции обозначается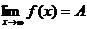

Число А называется пределом функции f(x) при х, стремящемся к 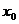(или в точке 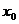), если для любого даже сколь угодно малого положительного числа 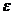>0, найдется такое положительное число 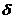>0, что для всех х, не равных 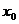и удовлет.условию 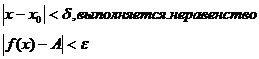,этот предел обозначается .

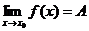Замечание 1. Определение предела не требует существования функции в самой точке 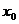.