Решение систем дифференциальных уравнений.

Системы дифференциальных уравнений операционным методом решаются также как и уравнения. Каждое дифференциальное уравнение переводится в операторное уравнение. Затем элементарный метод либо точка разложения находят искомые решения.

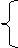
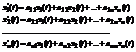
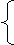
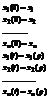
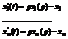
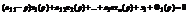
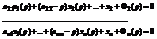
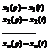
28. Применение операционного исчисления для расчета электрических цепей. Применение операционного метода исчисления основано на справедливости законов Кирхгофа для операторных тока и напряжения.Эти функции считают функциями оригиналами. Для различных элементов цепи справедливы следующие соотношения.

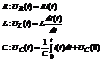
(1)

Переведем эти уравнения в операторные уравнения

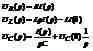
(2)

(3) , где 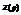- операторное сопротивление рассматриваемого участка цепи.

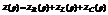
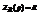
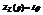
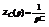
22. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.

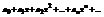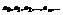Степенным рядом называется функциональный ряд вида , где - постоянные числа, называемые коэффициентами ряда.

Теорема Абеля.

Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком х, для которого .

Если ряд расходится при некотором значении 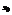, то он расходится при всяком х, для которого .

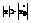Доказательство: Так как по предположению числовой ряд 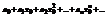сходится, то его общий член 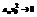при 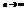, а это значит, что существует такое положительное число М, что все члены ряда по абсолютной величине меньше М. Перепишем ряд в виде 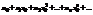и рассмотрим ряд из абсолютных величин его членов:

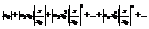Члены этого ряда меньше соответствующих членов ряда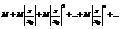

При 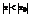последний ряд представляет собой геометрическую прогрессию со знаменателем 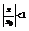и, следовательно, сходится.

Теперь нетрудно доказать и вторую часть теоремы: пусть в некоторой точке 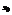ряд расходится. Тогда он будет расходиться в любой точке х, удовлетворяющей условию 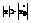. Действительно, если бы в какой-либо точке х-, удовлетворяющей этому условию, ряд сходился, то в силу только что доказанной первой части теоремы он должен был бы сходиться и в точке 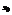, так как 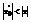. Но это противоречит условию, что в точке 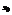ряд расходится. Следовательно, ряд расходится и в точке х. Теорема полностью доказана.

Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.

1. Двойной интеграл его опр. и св-ва:

Двойным интегр. от ф-ции f(x,y) по обл. D наз. предел, к которому стремится n-я интегр. сумма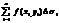

при стремлении к 0 наибольшего диаметра частичных обл..

Св-ва:1.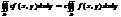

2.

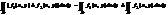
3.

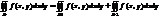
4. если f(x,y)>=0 ,то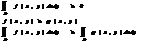

5.

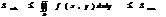
где S –площадь обл. D

6.

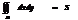
Вычисление двойного интеграла

Для вычисления дв. интегр применяется следующая ф-ла:

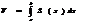
где S(х)-площю сечения плоскости ┴0х

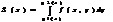
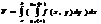
Замена переменных в двойн интегр . Якобиан.