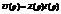Теорема о дифференцировании изображения
Теорема о дифференцировании изображения
Пусть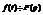 
, тогда дифференцированию изображения соответствует умножение оригинала на (-t)
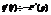
Поскольку F(p) аналогична, то она и дифференцируема
………………………….…..
.
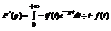
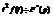
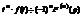34. Теорема об интегрировании изображения
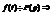
интегрированию изображение соответствует деление оригинала на t:
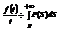
Док-во:
; 
;
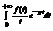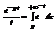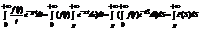
Пример: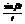 
.
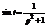
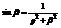
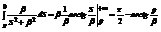37. Теорема Бореля об умножении изображений (о свертке)
Пусть функция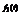 
- функция оригинал 
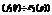, также функция 
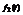- функция оригинал 
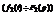, тогда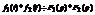 
Если вспомнить интеграл Лапласа:
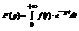
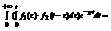
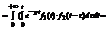
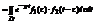=, где
Покажем порядок интегрирования, получим
= 
.
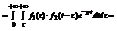
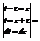
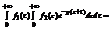
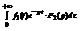
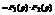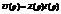
Вычисление двойного интеграла
Для вычисления дв. интегр применяется следующая ф-ла:
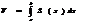
где S(х)-площю сечения плоскости ┴0х
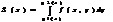
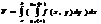
Замена переменных в двойн интегр . Якобиан.
Двойн интегр в полярных координатах
Введем замену переменных в 2-ом интегр х=φ(u,v)
Y= φ(u,v) если эти ф-ции лежат в обл. D
D<=0UV –непрерывн частные производные 1-ого порядка
и определитель
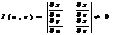
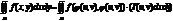
Замена полярных коорд. X=rcosφ Y=rsinφ –непрер. Диф ф-ции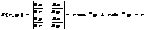 
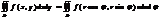
Приложения 2-ых интегралов
а) объем тела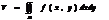 
б) площадь плоской фигуры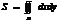 
в)масса плоской фигуры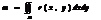 
г)Статические моменты и центр тяжести плоской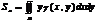 
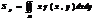
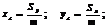
Ой интеграл, его св-ва и вычисление
3-ой интегр равен произедению значения подынтегр ф-ции в некоторой точке области интегрирования на объем област интегр.
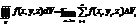
Св-ва 3-ого интеграла:
1. 
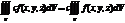
2. 
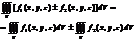
3. 
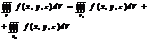4. 
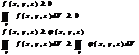
5. 
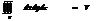
6. 
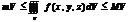
7. 
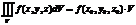
Замена переменных в 3-ом интегр. Цилиндрич и сферические координаты
Пусть: х=φ(u,v,w); Y= ψ(u,v,w); Z=λ(u,v,w)
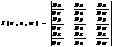
То справедлива ф-ла замены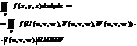 
Цилиндрические координаты:
Положение точки в пространстве OXYZ можно определить заданием 3-х чисел r, φ,z (цилиндрические координаты точки)
Заменяем x=rcos φ y=rsin φ z=z
Соответственно якобиан будет =r
Ф-ла замены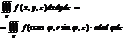 
Сферические координаты:
x=ρcosφsinӨ y=ρsinφcosӨ z=ρcosӨ
ρ>=0; 0<=φ<=2π; 0<=Ө<= π
I(ρ, φ, Ө)= ρ2sin Ө
Ф-ла замены
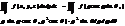
Приложение 3-ых интегралов
а)объем тела: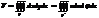 
б)масса тела: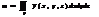 
γ(x,y,z)-поверхностная плотность
в)статистические моменты:
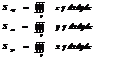
г)центр тяжести тела
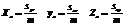
Криволинейный интеграл 1 рода, опр. ,
св-ва и вычисление:
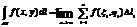
Св-ва криволин интегр 1 рода:
1. 
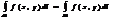
2. 
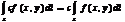
3. 
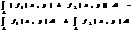
4. 
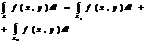
5. 
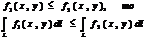
6. 
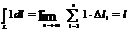
7. 
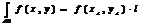
Вычисление кривол интегр 1-ого рода
а) параметрическое представление
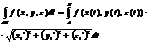
б) явное представление:
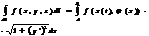
в) полярное представление:
Криволинейный интегр 2-ого рода, опр., св-ва и вычисление
Если кривая АВ гладкая , а ф-ция P(x,y) Q(x,y) непрерывны на прямой АВб то криволинейный интеграл 2-ого рода существует
Св-ва кр. интегр. 2-ого рода
1. 
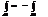
2. 
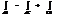
3. 
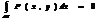
Если АВ лежит в плоскости ┴ оси ОХ
4. Криволинейные интегр по замкнутой кривой не зависит от выбора начальной точки
Пов. Инт. 1-го рода.Его св. и выч.
Пусть в точках пов. S С ПЛ. S пространства oxyz опред. Непрерывная ф. f(x,y.z) .
Разобьем пов. S на n частей Si, ПЛ. КАЖДОЙ ЧАСТИ дельта Si, а диаметр Di i=1..m в каждой части Si выберем произвольную точку Mi от (xi, yi, zi) и cоставим сумму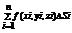 
. Сумма называется интегральной для ф. f(x,y.z) по поверхности S если при 
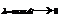интегр. Сумма имеет предел, то он наз. Пов интегралом 1-го родаот ф. f(x,y.z) по поверхности S и обозначается 
= 
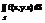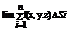
Свойства пов. Инт.
1) 
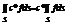, с=const
2) 
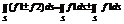3) S=s1+s2, Тогда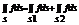 
4) f1<=f2 , т о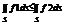 
5) 
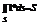6) 
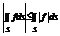7) Ф. f непрерывна на поверхности S , то на этой поверхности сущ. Точка M(x0,y0,z0) 
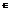S, такая , что 
.
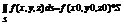Выч пов инт 1-го родасводиться к вычисленею2-го инт по обл Д, кот явл проекцией пов S на плоскость oxy, если пов s задана Ур z=z(x,y) то по винт равен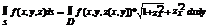 
.
Если S задано в виде y=y(x, z), то …
Пов инт 2-го рода
Пусть задана двусторонняя пов, после обхода такой пов не пересекая ее границы направление нормали к ней не меняется. Односторонныя пов: является Лист Мебиуса. Пусть в точке рассматриваемой двусторонней поверхности S в прстранстве oxyz определена ф. F(x,y,z). Выбронную сторону поверхности разбиваем на части Si i=1..m и проектируем их на корд плоскости. При этом пл пов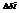 
,берем со знаком «+», если выбрана верхняя сторона пов ( если нормаль 
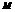образует острый угол с oz, выб со зн «–» если выбрана нижняя сторона пов( ТУПОЙ УГОЛ)). Составим инт сумму 
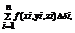Где 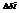– пл пов Si –части при 
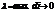если он сущ и не зависит от способа разбиения поверхности на части и от выбора точек в них, наз по инт 2-ого рода от ф. f(x,y,z) по пов s и обозначается: 
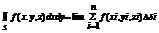по опред пов интеграл будет = пределу интегр суммы. Аналогично опред инт по пов s
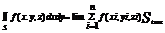
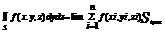, тогда общим видоим пов инт 2-го рода служит инт 
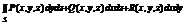где P, Q, R непрерывные функции опред в точках двусторонней пов s. Если S замкнутая пов, то по инт по внешней стороне обозначается 
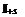и по внутренней стороне 
.
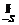Свойства по винт 2-го рода
1) Пов инт 2-го рода изм знак при перемене стороны пов 2) пост множетель можно выносить за знак инт 3) пов инт от суммы ф.равен суммен пов инт от слагаемых 4) по винт от всей пов S =S1+S2 равен сумме инт по ее частям S1и S2, если S1 иS2 пересек лишь по границе их разеляющей 5) если S1, S2 ,S3 цилиндрические поверхности с обр параллельными oz, ox, oy соотв, то пов инт: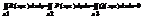 
Выч по винт 2-го рода
Пусть R(xyz) непрерывна во всех точках пов s задано Ур z=z(xy), где Z(xy) непрерывна в замкнутой области Дxy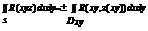 
Знак «+» если брать верхнюю сторону поверхности S, «–» если нижнюю.
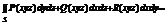
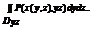Замеч Можно показать справедливость равенств dxdy=cos 
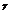ds, dydz=cos 
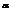ds, dxdz=cos 
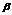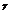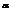ds. Где ds элемент площади пов S , а cos , cos cos 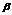напр cos нармали n. Выбранной стороны пов.
Формула Стокса
Если функции P(x,y,z),Q(x,y,z),R(x,y,z) непрерывны вместе со своими частными первого порядка в точках ориентированной поверхности S,то имеет место фо-ла:
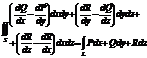
Где L-граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении(т.е.при обходе границы
L поверхность S должна остоваться все время с лева).
Циркуляция поля.
Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора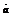 
на вектор 
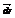, касательный к контуру L, называется циркуляцией вектора 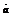вдоль L, т.е. 
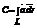. Рассмотрим различные формы записи циркуляции. Т.к.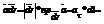 
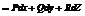. То 
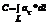или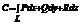 
. Циркуляция С имеет простой физический смысл: если кривая L расположена в силовом поле, то циркуляция - это работа силы 
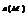поля при перемещении материальной точки вдоль L.
Ротор векторного поля.
Ротором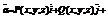 
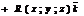называется вектор, обозначаемый 
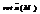и определяется формулой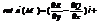 
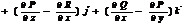
Формулу можно записать с помощью определителя:
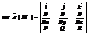
Свойства:
1 Если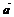 
- постоянный вектор, то 
.
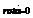2. 
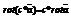, где c=const.
3. 
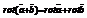, т.е.
Ротор суммы двух векторов равен сумме роторов слагаемых.
4. Если U – скалярная функция, а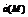 
- векторная, то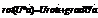 
Теорема о дифференцировании изображения
Пусть 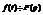, тогда дифференцированию изображения соответствует умножение оригинала на (-t)
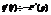
Поскольку F(p) аналогична, то она и дифференцируема
………………………….…..
.
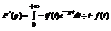
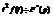
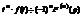34. Теорема об интегрировании изображения
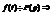
интегрированию изображение соответствует деление оригинала на t:
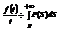
Док-во:
; ;
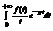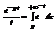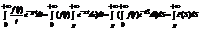
Пример: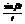
.
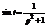
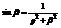
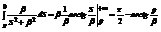37. Теорема Бореля об умножении изображений (о свертке)
Пусть функция 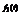- функция оригинал 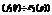, также функция 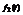- функция оригинал 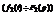, тогда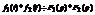
Если вспомнить интеграл Лапласа:
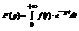
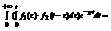
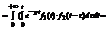
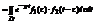=, где
Покажем порядок интегрирования, получим
=
.
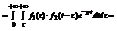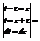
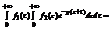
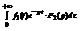
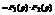