Основные теоремы о дифференцируемых функциях.

Основные теоремы о дифференцируемых функциях.

1)Теорема Ролля. Пусть на отрезке [a,b] определена ф-ция f(x) причем: f(x) непрерывна на [a,b]; f(x) диф. на (a,b); f(a)=f(b). Тогда $ т-ка сÎ(a,b), в которой f‘(c)=0.

2)Теорема Логранджа. Пусть на отрезке [a,b] определена f(x), причем: f(x) непр. на [a,b]; f(x) диф. на [a,b]. Тогда $ т-ка cÎ(a,b) такая, что справедлива ф-ла (f(b)-f(a))/b-a= f‘(c).

3)Теорема Коши. Пусть ф-ции f(x) и g(x) непр. на [a,b] и диф. на (a,b). Пусть кроме того, g`(x)¹0. Тогда $ т-ка сÎ(a,b) такая, что справедл. ф-ла (f(b)-f(a))/(g(b)-g(a))=f‘(c)/g‘(c).

Монотонность функции. Достаточное условие возрастания (убывания) функции.

Пусть ф-ия у= f(x) определена на Х и внутри этого мн-ва имеет конеч. производн. f ‘ (x), на (границе) концах сохр непрерывность,если конце принадл Х . Для того,чтобы f(x) была постоян на мн-ве Х чтоб выполн рав-во f ‘(x)=0 внутри мн-ва Х.

Убыв. и возраст. ф-ии назыв. монотонностью.

Достаточное условие возрастания(убывания): f(x) – возвраст. на Х, если для любых х1, х2 принадлеж. Х, х1<x2=>f(x1)<f(x2). f(x) – убыв. на Хó для любых х1,х2 принадлеж. Х, х1<x2=>f(x1)>f(x2).

Достаточное условие экстремума.

Max и min наз общ термином экстремума

Необходимый признак экстремума: ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.

Достаточный признак:1) точка х₀ является точкой экстремума,крит точкой 1 рода, если ее производная в этой точке меняет знак:- если при переходе слева напр производн меняет знак с “+” на “-”, то х₀- т. Max -если с “-” на “+”, то х₀- т. min – если при переходе знак не меняется,то т. х0—не явл экстремум 2) пусть х0 стационарн точка в которой ф-ия f(x) дважды дифференциров,тогда 1) если f’’(x0)<0 х0-max 2) если f’’(x0)>, x0-min Но 2-ым усл нельзя польз если 2-ая производн в т. х0 обращается в 0 или не сущ

Выпуклость, вогнутость и точки перегиба графика функции.

Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.

Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.

Достаточное усл выпукл и вогнутости)

Пусть функция f (x) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

-если f '' (x) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

-если f '' (x) < 0 для любого x (a, b), то функция f (x) является выпуклой на интервале (a, b) .

Признаки точки перегиба: чтобы X₀ была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х₀.

Асимптоты графика функции.

Прямая, к которой приближается график ф., но никогда не пересечёт её, называется асимптотой графика ф. Пусть y=kx+b называется асимптотой графика ф. f(x), при 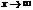, если 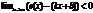. Коэффициент k и b вычисляются

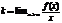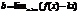; . Таким образом определяются горизонтальные и наклонные асимптоты. Чтобы определить вертикальную асимптоту, необходимо исследовать функцию в точке разрыва. Прямая x=a называется вертикальной асимптотой графика функции f(x), если 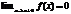или .

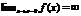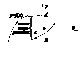разрыв ф-ции первого вида

Определение первообразной ф-ии и неопред интергала. Свойства неопределенного интеграла. Таблица основн интегралов.

Функция F(x) называется первообразнойфункции ƒ(х) на интервале (а; b), если для любого х є (а;b) выполняется равенство F'(x)=ƒ(x) (или dF(x)=ƒ(x)dx).

Множество всех пepвoобpaзныx функций F(x)+С для ƒ(х) называется неопределенным интегралом от функции ƒ(х) и обозначается символом ∫ ƒ(х) dx.

Таким образом, по определению ∫ƒ(x)dx= F(x)+C.

Св-ва..1. ( òf(х)dх)'= f(х) 2. dòf(х)dх)'=f(х)dх

3. òdF(х)=F(х)+С 4)òkf(х)dх=kòf(х)dх, k¹0.

5) ò(f(х)±g(х))dх= òf(х)dх±òg(х))

Таблица..1)ò0dх=С. 2.òхdх= х+С. 3. òх^adх= 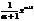+С, a¹1.4) òсоsхdх=sinх+С, 5. òsinхdх= –соsх+С;

6) ò 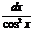=tgх+С; 7. ò 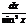=-сtgх+С;

8)ò 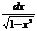= 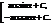; 8а. ò = ;

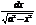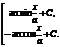9)ò 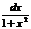= 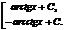; 9а. ò = ;

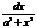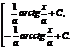10)òа^хdх=а^х/lnх+С; 10а. òе^хdх= е^х + С;

11)ò 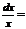ln|х|+С; 12. ò 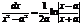+С;

13 ò 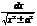=ln|х+ 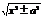|+С

12. Замена переменной (подстановка) в неопределённом интеграле. Интегрирование по частям.

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:

а) 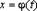, где – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае: ;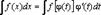

б) 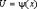, где U – новая переменная. Формула замены переменной при такой подстановке: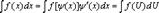

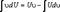
Нахождение интеграла по формуле

называется интегрированием по частям. Здесь U=U(х),υ=υ( x) непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла сводится к отысканию другого интеграла 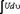,ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен. При этом за υ берется такая функция, которая при дифференцировании упрощается, а за dU – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Ф-ла замены переменной:

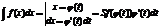
Длина дуги плоской кривой.

Пусть некот. линия y=f(x), где f(x) – дифф. на отрезке [a; b]

Y(k-1) M(k-1)

M1

yk A Mk

M(n-1) B

a=x0 x1 x2 xk x(n-1) b=xn 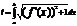- длина дуги АВ

Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой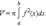

Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен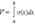

Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как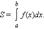

Дифференциальные уравнения.

1) Уравнение вида F(х,у,у’,у’’…у^n)=0 наз обыкновенным дифф. Уравнен n-ого порядка,или просто дифференц уравнен n-ого порядка.

2) Решением ур (1) наз ф-ия y=f (фи)(х) удовлетворяющ уравнению (1),т.е. такая,для которой выполн тождество F(x,f(x), f’(x)…f(x)^n)=0

3) График решения дифф уравн наз интегральн кривой.

4) дифф ур 1-ого порядка наз уравн вида F(x,y,y’)=0

Предполож что это уравнен можно решить относит y’=F(х,у) (3)

5) общим решением дифф уравн (3) наз такая ф-ия у=фи(х,с),котор при каждом значении с из некоторого мн-ва явл решен ур (3)

6) те решения дифф уравн которые получ из общего решения путём фиксирования произвольн постоян наз частной.

Необх признак

Если ряд 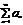- сход., то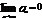

Док-во:

, ,

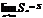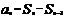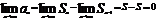
Данный признак означает, что если 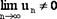то ряд расходится. Но условие 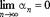явл необходим,но недостаточным,т.е из выполн данных услов не всегда следует сходимость рядов

Теорема Абеля

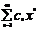(4)

1)Если степенной ряд сходится при х=х0, u≠0,то он сходится абсолютно при всех |x|<|x0|

2)если при х=х1 степенн ряд расход,то он расход при всех |x|>|x1|

Если ряд 4 сход. в некот. т. х1≠0, то он будит сход. при всех знач.-ях х принадлеж. R. |x|<|x1|.

Если ряд 4 расход, в x2, то он будит расходящимся и при всех х принадлеж. R, |x|>|x2|.

Ряды Тейлора и Маклорена

Пусть f(x) имеет производные всех порядков некотор. окрестн. т. x. Рядом Тейлора для f(x) в т. х0 назыв. степен. ряд след. вида: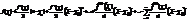

Если х0=0, то ряд 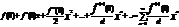назыв. рядом Маклорена

При выполнении некотр. условий ряд Тейлора для f(x) равен самой f(x). Говорят, что ф-ия представима в виде ф-ии степен. ряда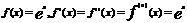

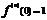
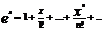x принадлеж. R.

3.Разложение функции y=cosx в ряд Маклорена.Дифференцируя ряд (33), получаем разложение при x (-∞;+∞):

cosx=1- .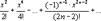

4/Разложить в ряд Маклорена функцию f(x)=ln(1+x).

Проинтегрируем обе части равенства (37) от 0 до x при x (-1;1). Получим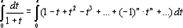

или

ln(1+x)=x .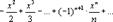

Можно показать, что ряд имеет область сходимости (-1;1].

39. Разложение ф-ий sinx, cosx, e^x, ln(1+x) в ряд Маклорена

Разложение функции f(x)=ex в ряд Маклорена.

f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex.

f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1.

Составим для функции f(x)=ex формально ряд Маклорена: 1+

Найдём области сходимости этого ряда.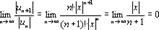

при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то 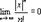при любых х и тем более 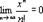при любых х. Так как f^(n+1)(x)=ex и f^(n+1)(с)=e^с, то 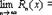=e^c=0. Таким образом, имеет место разложение при x(-∞;+∞)

e^x=1+ .

Разложение функции f(x)=sinx в ряд Маклорена.

Вычислим производные данной функции.

f′(x)=cosx=sin(x+ ), f″(x)=-sinx=sin(x+ ),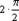

f″′(x)=-cosx=sin(x+ 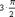), f(4)(x)=sinx=sin(x+ 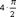), …, f(n)(x)=sin(x+ 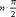), … . Вычислим значения f(x) и производных в точке 0: f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f^(4)(0)=0, …, f^(2n-1)(0)=(-1)^n-1, f^(2n)(0)=0.

Исследуем остаточный член ряда.

|Rn(x)|= 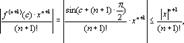= так как |sin(c+(n+1) |≤1. Переходя к пределу при n→∞, получаем 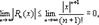следовательно, 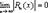и 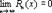. Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x (-∞;+∞):

sinx=x- .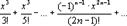

Основные теоремы о дифференцируемых функциях.

1)Теорема Ролля. Пусть на отрезке [a,b] определена ф-ция f(x) причем: f(x) непрерывна на [a,b]; f(x) диф. на (a,b); f(a)=f(b). Тогда $ т-ка сÎ(a,b), в которой f‘(c)=0.

2)Теорема Логранджа. Пусть на отрезке [a,b] определена f(x), причем: f(x) непр. на [a,b]; f(x) диф. на [a,b]. Тогда $ т-ка cÎ(a,b) такая, что справедлива ф-ла (f(b)-f(a))/b-a= f‘(c).

3)Теорема Коши. Пусть ф-ции f(x) и g(x) непр. на [a,b] и диф. на (a,b). Пусть кроме того, g`(x)¹0. Тогда $ т-ка сÎ(a,b) такая, что справедл. ф-ла (f(b)-f(a))/(g(b)-g(a))=f‘(c)/g‘(c).