Тема 3 Векторная алгебра и аналитическая геометрия
В пространстве
Задача 4. Даны координаты трех точек: A(3; 0; -5), В,(6; 2; 1),С(12; -12; 3).
Требуется: 1) записать векторы 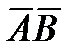 и
и 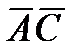 в системе орт и найти модули этих векторов; 2) найти угол между векторами
в системе орт и найти модули этих векторов; 2) найти угол между векторами 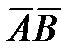 и
и 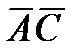 ; 3) составить уравнение плоскости, проходящей через точку С перепендикулярно вектору
; 3) составить уравнение плоскости, проходящей через точку С перепендикулярно вектору 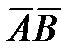 .
.
Решение. 1. Если даны точки М1(х1, у1, z1) и М2 (х2, у2, z2), то вектор 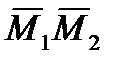 через орты
через орты 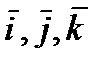 выражается следующим образом:
выражается следующим образом:
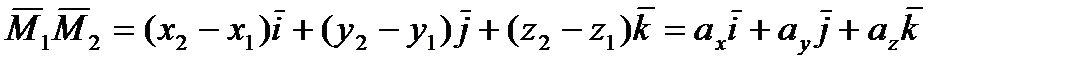 (1)
(1)
Подставляя в эту формулу координаты точек А и В, имеем:
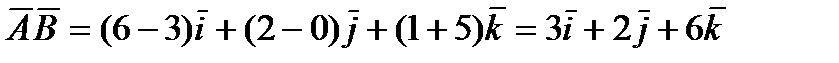
Подобным образом 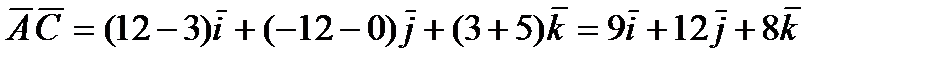
Модуль вектора 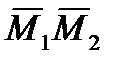 вычисляется по формуле:
вычисляется по формуле:
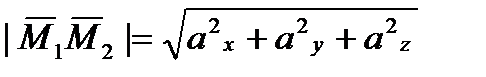 (2)
(2)
Подставляя в формулу (2) найденные ранее координаты векторов 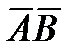 и
и 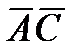 , находим их модули:
, находим их модули:
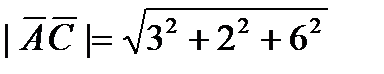
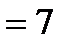
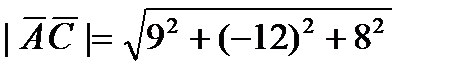 =17
=17
2. Косинус угла 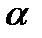 , образованного векторами
, образованного векторами 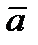 и
и 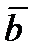 , равен их скалярному произведению, деленному на произведение их модулей:
, равен их скалярному произведению, деленному на произведение их модулей:
cos 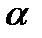 =
= 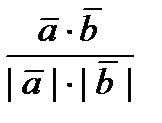 (3)
(3)
Так как скалярное произведение двух векторов, заданных своими координатами равно сумме попарныx произведений одноименных координат, то
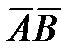 *
* 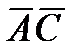 = 3*9+2*(-12)+6*8=51.
= 3*9+2*(-12)+6*8=51.
Применяя (3), имеем: сos 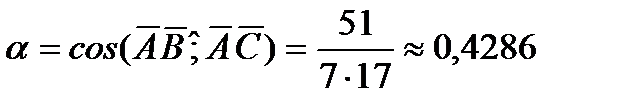
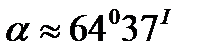
3. Известно, что уравнение плоскости, проходящей через точку М0(х0, у0, z0) перпендикулярно вектору 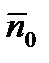 А; В; С имеет вид
А; В; С имеет вид
A(x – хо) +B(y – уо) + С(z – zо) =0 (4)
По условию задачи искомая плоскость проходит через точку С(12; - 12; 3) перпендикулярно вектору 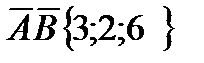
Подставляя в (4) А=3, В=2, С=6, хо = 12, уо = - 12, zо =3, получим:
3(х – 12)+2(у+12) +6(z – 3) = 0, Зх + 2у + 6z – 30=0 — искомое уравнение плоскости.
Вопросы для самопроверки
1. Какие величины называются скалярными, векторными?
2. Какие векторы навязываются коллинеарными?
3. Какие два вектора называются равными?
4. Как сложить два вектора? Как их вычесть?
5. Как найти координаты вектора по координатам точек его начала и конца?
6. Назовите правила сложения, вычитания векторов, заданных в координатной форме. Как умножить вектор на скаляр?
7. Дайте определение скалярного произведения двух векторов. Перечислите основные свойства скалярного произведения.
8. Как найти скалярное произведение двух векторов по их координатам?
9. Напишите формулу для определения угла между двумя векторами.
10.Напишите условия: коллинеарности двух векторов; их перпен-дикулярности.
11. Напишите общее уравнение плоскости.
12. Напишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
13.Какой вид имеет уравнение плоскости, проходящей через три данные точки?
14.Напишите формулу для определения расстояния от точки до плоскости.
Вопросы для самопроверки
1. Что называется определителем второго, третьего, n-го порядков?
2. Назовите основные свойства определителей.
3. Что называется минором, алгебраическим дополнением элемента определителя?
4. Напишите формулы Крамера решения системы линейных уравнений. В каких случаях их можно использовать?
5. Назовите схему решения системы линейных уравнений по методу Гаусса.
6. Что называется матрицей?
7. Как определяются основные действия над матрицами?
8. Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной?
9. Что называется рангом матрицы? Как найти ранг матрицы?
10. Сформулируйте теорему Кронекера - Капелли.
11. Опишите матричный способ решения системы линейных уравнений.
12. Какова геометрическая интерпретация систем линейных уравнений и неравенств?
Тема 4 Введение в анализ
Разберите решение задач 6, 7 данного пособия.
Задача 6. Вычислить пределы:
a) 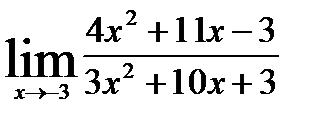 , б)
, б) 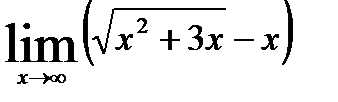
в). 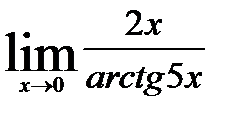 г)
г) 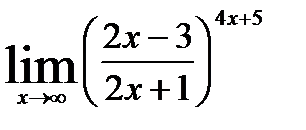
Решение. a) Подстановка предельного значения аргумента х= -3 приводит кнеопределенному выражению вида 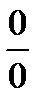 . Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при
. Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при 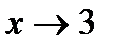 :
:
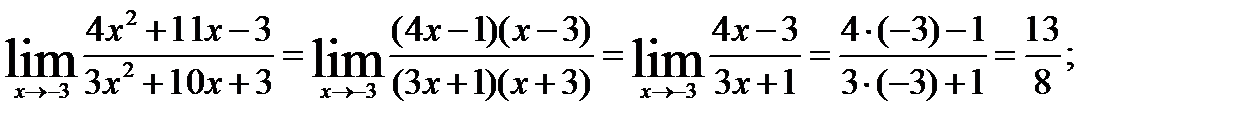
б). При 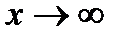 выражение
выражение 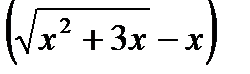 дает неопределенность вида
дает неопределенность вида 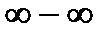 . Для ее устранения умножим и разделим это выражение на
. Для ее устранения умножим и разделим это выражение на 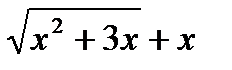
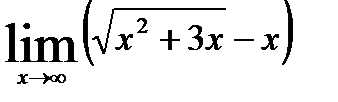 =
= 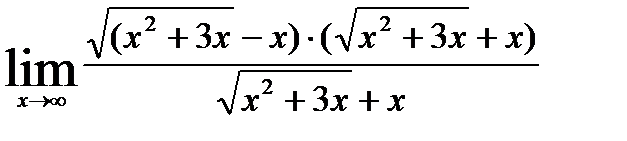 =
= 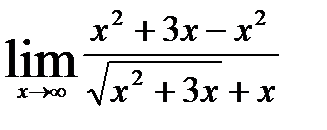 =
= 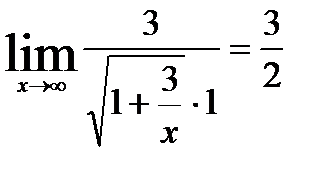 ;
;
в). Обозначим arctg5x=y. Тогда 5x=tg y и 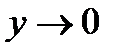 при
при 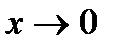 . Применяя свойства пределов и формулу первого замечательного предела
. Применяя свойства пределов и формулу первого замечательного предела 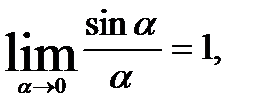 имеем:
имеем:
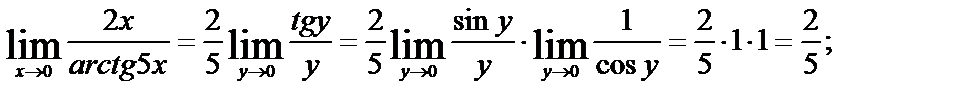
г). При 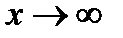 выражается
выражается 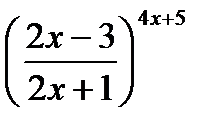 является неопределенностью вида
является неопределенностью вида 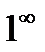 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при 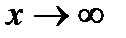 величины и применим формулу второго замечательного предела:
величины и применим формулу второго замечательного предела: 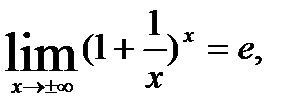
тогда имеем: 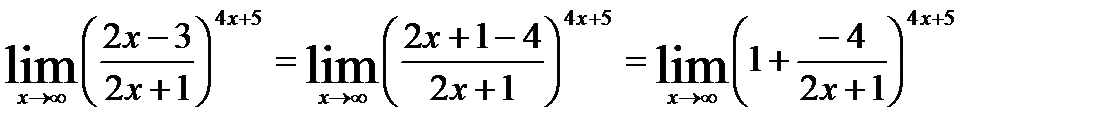
Пусть 2x+1=-4y. Тогда 4x+5=-8y+3 и 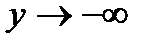 при
при 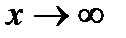 . Переходя к переменной y, получим:
. Переходя к переменной y, получим:
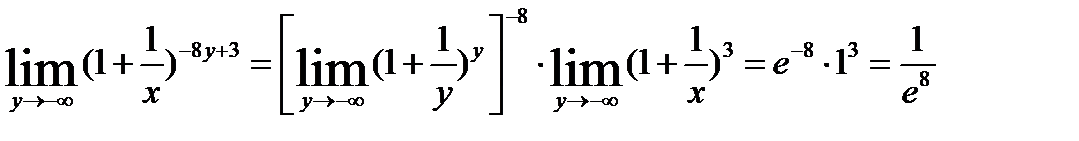
Задача 7. Исследовать на непрерывность функцию 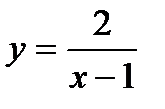 .
.
Решение. Данная функция является элементарной. Известно, что всякая элемен-тарная функция непрерывна на своей области определения. Данная функция определена на интервалах ( - 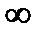 ; 1) и (1;
; 1) и (1; 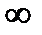 ) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 4.
) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 4.
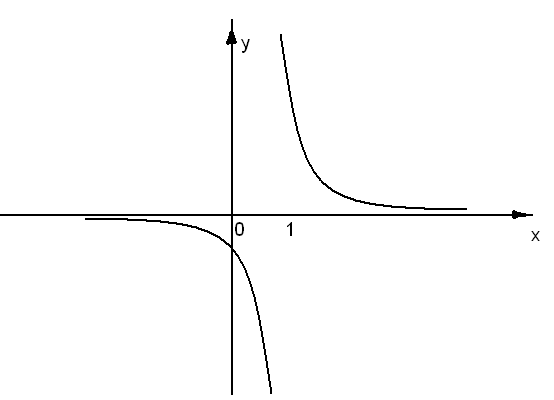
Рис. 4
Вопросы для самопроверки
1. Сформулируйте определение понятия функции.
2. Что называется областью определения функции? Областью изменения функции?
3. Перечислите основные элементарные функции. Назовите их основные свойства.
4. Какие функции называются элементарными? Приведите примеры.
5. Что называется пределом числовой последовательности?
6. Сформулируйте определение предела функции.
7. Назовите основные свойства пределов функций.
8. Какая функция называется бесконечно малой? Бесконечно большой?
9. Назовите свойства бесконечно малых функций.
10. Напишите формулы первого и второго замечательных пределов.
11. Какие логарифмы называются натуральными?
12. Дайте определение односторонних пределов функции в точке.
13. Какая функция называется непрерывной в точке? На интервале?
14. Какая точка называется точкой разрыва первого рода? Второго рода?
15. Перечислите основные свойства непрерывных на отрезке функций.
