Функция распределения одномерной случайной величины, определение, вывод свойств (включая формулу вероятности попадания в промежуток).

Случайной величиной ξ в данном опыте называется переменная величина, которая в результате испытания примет одно из своих возможных значений, но какое именно до проведения опыта неизвестно.

Спектр - совокупность всех возможных значений случайной величины.

Дискретный спектр - все возможные значения случайной величины образуют конечную или бесконечную последовательность.

Непрерывный спектр - все значения случайной величины заполняют сплошь некоторый промежуток.

Функцией распределения F(x) случайной величины ξ называется вероятность того, что случайная величина ξ в результате испытания примет значение, меньшее х, т.е.

F(x)=P(ξ<x).

Свойства F(x):

1) область определения F(x) - интервал (-бескон; +бескон))

2) 0 < F(x) £ 1,

3) F(-¥)=0, т.к. P(ξ<- ¥)=P(Q)=0,

4) F(+¥)=1, т.к. P(ξ<+ ¥)=P(W)=1,

5) F(x)- неубывающая функция.

Будем считать, что F(x) непрерывна слева

Вероятность попадания случайной величины в промежуток и в точку

Основное свойство функции распределения

Р(a£ξ<b)=F(b)-F(a).

Вероятность попадания случайной величины в заданный интервал равна разности значений функции распределения в концах интервала

Функция распределения одномерной случайной величины, определение, доказательства свойств (включая формулу вероятности попадания в промежуток).

Функцией распределения F(x) случайной величины ξ называется вероятность того, что случайная величина ξ в результате испытания примет значение, меньшее х, т.е.

F(x)=P(ξ<x).

Свойства F(x):

1) область определения F(x) - интервал

2) 0 < F(x) £ 1,

3) F(-¥)=0, т.к. P(ξ<- ¥)=P(Ø)=0,

4) F(+¥)=1, т.к. P(ξ<+ ¥)=P(W)=1,

F(x)- неубывающая функция.

Будем считать, что F(x) непрерывна слева

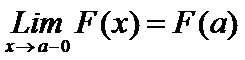
Вероятность попадания случайной величины в промежуток и в точку

Основное свойство функции распределения

Р(a£ξ<b)=F(b) – F(a).

Вероятность попадания случайной величины в заданный интервал равна разности значений функции распределения в концах интервала

Следствие:

Р(ξ=a) =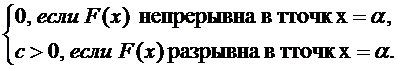

Действительно:

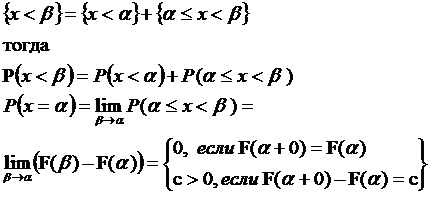
Замечание

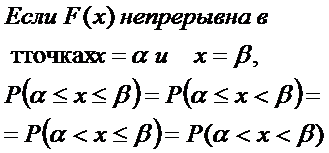
Функция распределения случайной величины ξ

F(x)=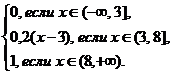

Найти вероятность попадания случайной величины ξ в интервал (1;6).

РешениеР(1<ξ<6)=F(6)-F(1)=0,2(6-3)-0=0,6.4

Дисперсия и среднеквадратическое отклонение случайной величины, формула для дискретного распределения, доказательство свойств дисперсии.

Дисперсией D(ξ) случайной величины ξ называется математическое ожидание квадрата ее отклонения от математического ожидания:

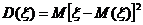
Среднее квадратическое отклонение

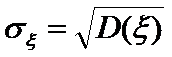
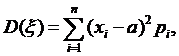
Свойства дисперсии

1. D(C) = 0

2. D(kξ) = k²D(ξ)

3. D(ξ) = M(ξ²) – [M(ξ)]²

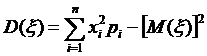
Пример:

D(ξ) = 13,61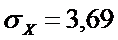

D(η) = 4,17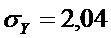

Основные распределения дискретной случайной величины

• Вырожденное распределение

• Распределение Бернулли

• Дискретное равномерное распределение

• Биномиальное распределение Р_n(m) = C_n^m p ^mq^n-m, где m=0;1;2;...,n и q=1-p.

• Гипергеометрическое распределение

• Геометрическое распределение

• Распределение Пуассона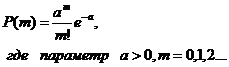

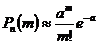
Биномиальное распределение. Формула вероятности, интерпретация, математическое ожидание с выводом, дисперсия.

Биномиальное распределение

Биномиальным распределением называется распределение дискретной случайной величины ξ = m, для которой ряд распределения задается формулой Бернулли

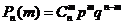
где m=0;1;2;...,n и q=1–p.

Биномиальное распределение имеет дискретная случайная величина ξ – число появлений события А в n независимых испытаниях, если вероятность появления события А в каждом испытании постоянна и равна р, и, следовательно, вероятность непоявления событияА в каждом испытании равна q=1–p.