Выпуклость и точки перегиба. Асимптоты графика функции.

49¹. Выпуклость и точки перегиба.

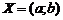Выпуклость графика функции. Пусть функция дифференцируема на интервале . Тогда в каждой точке ее графика существует касательная. График функции 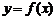называется выпуклым вверх (вогнутым вниз) на интервале X, если он целиком расположен ниже касательной в его произвольной точке; график функции 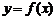называется выпуклым вниз (вогнутым вверх) на данном интервале, если он целиком расположен выше касательной в его произвольной точке.

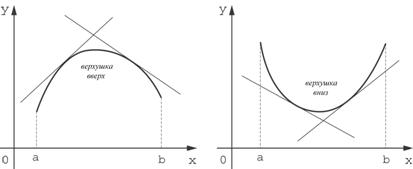
Рис. 1

Утверждение1. Если функция 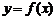имеет на интервале 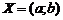вторую производную 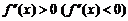во всех точках 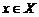, то ее график является выпуклым вниз (вверх) на этом интервале.

Точки перегиба графика функции. Говорят, что график непрерывной функции имеет при 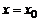точку перегиба, если слева и справа от точки 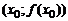график функции имеет разные направления выпуклости.

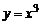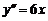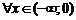Так, например, точка (0;0) является точкой перегиба графика функции . Так как и имеем ,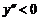
а 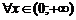получаем 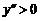, то на 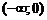график функции 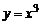– выпуклый вверх, а на 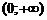– выпуклый вниз, и точка 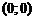является точкой, разделяющей промежутки выпуклости графика разной направленности, т.е. является точкой перегиба графика функции .

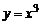Утверждение 2. Если в точке 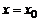вторая производная функции 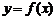обращается в нуль и при переходе через нее меняет знак, то 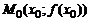– точка перегиба графика этой функции.

49². Асимптоты графика функции.

Асимптоты графика функции.Говорят, что прямая 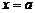является вертикальной асимптотой графика функции 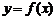, если хотя бы один из односторонних пределов 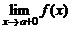или 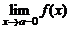равен 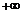или .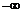

Так, график функции 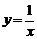имеет вертикальную асимптоту 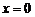, потому что .

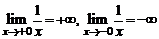Предположим, что функция определена на промежутке .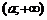

Говорят, что прямая 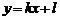является наклонной асимптотой графика функции при 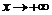, если функция представима в виде

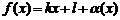, (4)

где 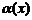– бесконечно малая функция при 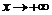, что означает неограниченное приближение графика функции к прямой, являющейся его асимптотой.

Утверждение 3. Для того, чтобы график функции имел асимптоту при 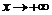, необходимо и достаточно, чтобы существовали конечные пределы:

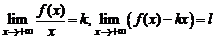. (5)

При выполнении условий (5) прямая 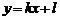является асимптотой.

Аналогично определяется наклонная асимптота графика функции при .

Общая схема исследования функции и построения её графика.

Для полного исследования поведения функций и построения их графиков рекомендуется следующее:

1) найти область определения функции;

2) найти точки разрыва функции, вертикальные асимптоты (если существуют), точки пересечения с осями координат;

3) определить четность (нечетность), периодичность функции;

4) найти промежутки монотонности функции и точки локального экстремума;

5) определить промежутки выпуклости графика функции и точки его перегиба;

6) найти наклонные асимптоты (если существуют);

7) на основании полученных данных построить график функции (иногда полученные данные сводят в таблицу).