Абсолютная величина (модуль) действительного числа.

Определение. Абсолютной величиной (или модулем) действительного числа а называется неотрицательное действительное число, удовлетворяющее условиям:

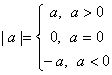
Из определения следует, что а ≤ │а│ для любого а.

Свойства абсолютных величин.

1. Абсолютная величина алгебраической суммы нескольких действительных чисел не больше суммы абсолютных величин слагаемых

.

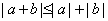2. Абсолютная величина разности не меньше абсолютных величин уменьшаемого и вычитаемого

> .

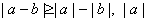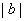3. Абсолютная величина произведения равна произведению абсолютных величин

.

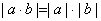4. Абсолютная величина частного равна частному абсолютных величин делимого и делителя

.

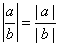Ограниченные и неограниченные числовые множества. 33⁴. Верхняя и нижняя грани числового множества.

Числовое множество А называется ограниченным сверху (снизу), если существует такое действительное число М (число т), что для каждого элемента х числового множества выполняется неравенство х≤M.При этом число М называется верхней границей (нижней границей) числового множества А. Геометрически это означает, что множество А расположено целиком слева от точки М, при этом не исключается, что сама точка М входит в А.

Числовое множество В называется ограниченным сверху, если существует такое действительное число m, что для каждого элемента х числового множества В выполняется неравенство х≥m. Число m называется нижней границей числового множества В. Множество В расположено целиком справа, от точки m, причем точка m может входить в него.

Ограниченное сверху числовое множество А имеет бесконечно много верхних границ.В самом деле, если М₁ является верхней границей множества А, то любое действительное число M₁>M₁ также является верхней границей множества А, так как для каждого элемента хƐА множества А выполняется неравенство х≤M₂.Аналогичное замечание можно сделать в отношении нижних границ ограниченного снизу множества.

Наименьшая из всех верхних границ ограниченного сверху числового множества А называется верхней гранью этого множества.

Наибольшая из всех нижних границ ограниченного снизу числового множества В называется нижней гранью этого множества.Иногда верхнюю (нижнюю) грань множества называют точной верхней (нижней) гранью множества.

К примеру, у множества отрицательных действительных чисел существует верхняя грань — число нуль, причем это число не принадлежит указанному множеству.

У множества натуральных чисел N существует нижняя грань , которая принадлежит указанному множеству.

Таким образом, верхняя (нижняя) грань числового множества может как принадлежать, так и не принадлежать этому множеству.

Числовое множество А называется ограниченным, если оно ограничено и снизу и сверху. Заметим, что любой отрезок является ограниченным множеством, так как нижней гранью этого множества является левый конец отрезка, а верхней гранью — правый конец. Неограниченные числовые множества не имеют хотя бы одной из границ. Примером неограниченного множества является любой неограниченный промежуток. Поэтому целесообразно множество упорядоченных пар действительных чисел называть числовой плоскостью, а любую упорядоченную пару — точкой числовой плоскости.

Теорема 1: Если непустое множество действительных чисел является ограниченным сверху (снизу), то оно имеет точную верхнюю (нижнюю) границу.

33³. Наибольший и наименьший элементы числового множества.

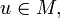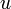Пусть и - верхняя грань 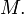Тогда 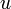называется наибольшим или максимальным элементом множества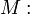

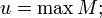
Пусть 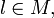и 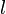- нижняя грань 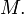Тогда 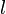называется наименьшим или минимальным элементом множества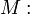

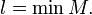
Наибольший и наименьший элемент множества, если они существуют, единственны.