Евклидово пространство. Неравенство Буняковского-Коши. Ортогональный и ортонормированный базисы. Разложение вектора по ортогональному базису.

26¹. Евклидово пространство. 26². Неравенство Буняковского-Коши.

1⁰. Определение евклидова пространства.В линейном пространстве 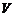кроме операций сложения элементов и умножения элемента на действительное число, введем еще одну операцию – скалярное произведение. Каждой паре векторов 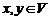сопоставим действительное число 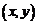, которое и назовем скалярным произведением.

Потребуем, чтобы для любых 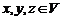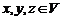и любого числа 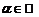выполнялись следующие аксиомы:

1) ;

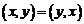2) ;

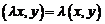3) ;

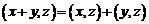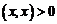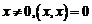4) при для .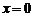

Очевидно, что скалярное произведение равно нулю, если хотя бы один из векторов нулевой: 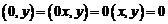. Скалярное произведение 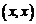вектора 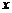на себя называют скалярным квадратом этого вектора.

Евклидовым пространством называется линейное действительное пространство, в котором задана операция скалярного умножения векторов, удовлетворяющая аксиомам 1) – 4).

В качестве примера евклидова пространства рассмотрим n-мерное линейное пространство 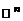упорядоченных совокупностей n действительных чисел. Скалярное произведение двух его векторов 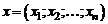, , 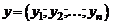по аналогии со случаями 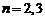, определим как

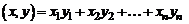. (1)

Рассматриваемое линейное пространство со скалярным произведением (1) называется n-мерным евклидовым пространством 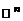(сохраним для него прежнее обозначение).

2⁰. Норма вектора евклидова пространства. Нормой вектора 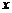евклидова пространства называется арифметическое значение корня из скалярного квадрата 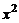этого вектора:

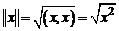. (2)

Например, в евклидовом пространстве 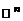норма вектора 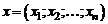определяется формулой

.

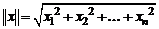Свойства нормы вектора .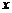

1. 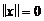в том и только в том случае, когда .

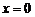2. 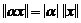, где 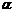– любое действительное число.

3. 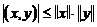— неравенство Коши-Буняковского.

4. 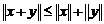— неравенство треугольника.

26³. Ортогональный и ортонормированный базисы.

Векторы x и y евклидова пространства V называются ортогональными 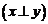, если выполняется условие .

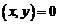Так как в геометрическом пространстве свободных векторов 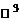понятие ортогональности совпадает с понятием перпендикулярности векторов, то ортогональность можно рассматривать как обобщение понятия перпендикулярности в абстрактном евклидовом пространстве.

Система векторов

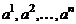(1)

называется ортогональной, если ее векторы попарно ортогональны,
т.е. 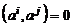при .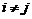

Утверждение 1. Ортогональная система, состоящая из ненулевых векторов, является линейно независимой.

Пусть теперь 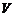– n-мерное евклидово пространство. Тогда, в силу утверждения 1, ортогональная система векторов (1) образует ортогональный базис этого пространства.

Вектор x евклидова пространства V назовем нормированным или единичным, если .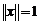

Если x – ненулевой вектор, то его можно нормировать, если умножить на число .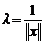

Система векторов 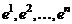называется ортонормированной, если она является ортогональной и нормированной.

Базис n-мерного евклидова пространства V называется ортонормированным, если базисные векторы образуют ортонормированную систему.

Теорема 1. В n-мерном евклидовом пространстве V существует ортонормированный базис.

Скалярное произведение двух векторов, заданных координатами в ортонормированном базисе, равно сумме произведений одноименных координат.

Отсюда, .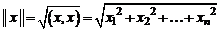

26⁴. Разложение вектора по ортогональному базису.

разложение вектора по ортогональному базису:

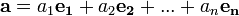
Коэффициенты можно найти так:

.
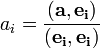