Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью.
191. Угол между прямой и плоскостью.
Пусть дана прямая, заданная каноническими уравнениями
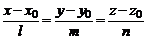 (1)
(1)
и плоскость
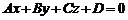 . (2)
. (2)
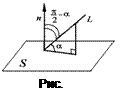 Углом между прямой
Углом между прямой 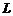 и плоскостью
и плоскостью 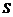 считают острый угол
считают острый угол 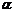 между этой прямой и ее проекцией на плоскость
между этой прямой и ее проекцией на плоскость 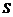 (рис.1).
(рис.1).
Этот угол определяется равенством
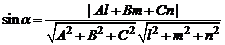 .
.
192. Взаимное расположение прямой и плоскости.
Прямая (1) параллельна плоскости (2) тогда и только тогда, когда направляющий вектор этой прямой 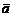 перпендикулярен нормальному вектору
перпендикулярен нормальному вектору 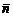 данной плоскости.
данной плоскости.
Отсюда получаем условие параллельности прямой (1) и
плоскости (2):
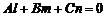 .
.
Прямая (1) перпендикулярна плоскости (2) в том и только том случае, когда направляющий вектор 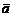 этой прямой коллинеарен нормальному вектору
этой прямой коллинеарен нормальному вектору 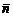 плоскости, что равносильно следующему равенству:
плоскости, что равносильно следующему равенству:
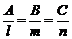 .
.
Найдем теперь условия, при которых прямая (1) принадлежит плоскости (2). Это будет тогда и только тогда, когда одновременно будут выполняться два равенства:
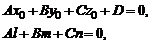 (3)
(3)
где первое из равенств (3) означает, что точка 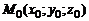 , через которую проходит прямая (1), принадлежит плоскости (2), а второе равенство из (3) выражает условие параллельности прямой (1) и плоскости (2).
, через которую проходит прямая (1), принадлежит плоскости (2), а второе равенство из (3) выражает условие параллельности прямой (1) и плоскости (2).
Кониченские поверхности.
Конической называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и проходящей через некоторую точку (вершину). Уравнение конуса второго порядка с вершиной в начале координат, осью которого служит ось Oz, записывается в виде
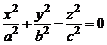 . (5)
. (5)
Геометрически коническую поверхность можно изобразить, как показано на рис. 4.
Аналогично, уравнения 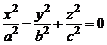 ,
, 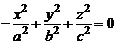 являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.
являются уравнениями конусов второго порядка с вершиной в начале координат, осями которых служат соответственно оси Оу, Ох.
Цилиндрические поверхности.
Поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной некоторому заданному направлению, называется цилиндрической.
Уравнение вида 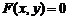 в декартовой системе координат
в декартовой системе координат
в пространстве определяет цилиндрическую поверхность, у которой образующие параллельны оси Oz. Аналогично, уравнение 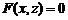 определяет цилиндрическую поверхность с образующими параллельными оси Oy, а
определяет цилиндрическую поверхность с образующими параллельными оси Oy, а 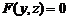 – цилиндрическую поверхность с образующими параллельными оси Ох.
– цилиндрическую поверхность с образующими параллельными оси Ох.
Канонические уравнения цилиндров второго порядка:
эллиптический цилиндр
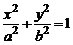 , (2)
, (2)
гиперболический цилиндр
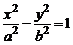 , (3)
, (3)
параболический цилиндр
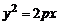 . (4)
. (4)
Образующие всех трех цилиндров, определяемых уравнениями (2), (3), (4), параллельны оси Oz, а направляющей служит соответствующая кривая второго порядка (эллипс, гипербола, парабола), лежащая в плоскости Oxy.
Отметим, что кривую в пространстве можно задать либо параметрически, либо в виде линии пересечения двух поверхностей. Например, уравнения направляющей эллиптического цилиндра, т.е. уравнения эллипса в плоскости Oxy, имеют вид
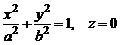 .
.
Эллипсоид.
Эллипсоидом (рис. 1) называется поверхность, определяемая в декартовой системе координат Oxyz каноническим уравнением
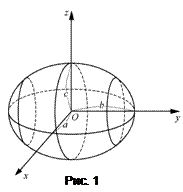
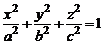 , (1)
, (1)
где величины а, b, c называют полуосями эллипсоида.
Из уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат – центром симметрии.
Точки пересечения осей координат с эллипсоидом называют вершинами эллипсоида.
Рассмотрим сечение эллипсоида плоскостью 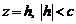 , параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений:
, параллельной плоскости Оху. Тогда линия, которая получается в сечении, определяется системой уравнений:
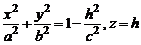 . (2)
. (2)
Обозначим 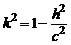 и перепишем (2) в виде
и перепишем (2) в виде 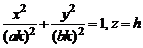 .
.
Таким образом, сечение эллипсоида (1) плоскостью 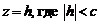 , представляет собой эллипс с полуосями ak и bk. Если
, представляет собой эллипс с полуосями ak и bk. Если 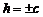 , то этот эллипс стягивается в точку – вершину эллипсоида (0;0;+с) или
, то этот эллипс стягивается в точку – вершину эллипсоида (0;0;+с) или 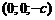 .
.
Аналогичная картина получается при рассмотрении сечений эллипсоида плоскостями, параллельными координатным плоскостям Oxz и Oyz. Заметим только, что плоскость Oхz пересекает эллипсоид по эллипсу, который определяется системой
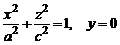 ,
,
плоскость Oyz – по эллипсу, определяемому уравнениями
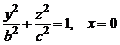 .
.
Если две полуоси эллипсоида равны, например 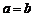 , из (1) получаем уравнение
, из (1) получаем уравнение
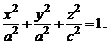 (3)
(3)
Если пересечь эллипсоид (3) плоскостью 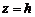 , то получим окружность
, то получим окружность
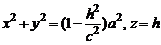
с центром на оси Oz. Поэтому такой эллипсоид можно получить вращением расположенного в плоскости Oхz эллипса 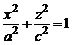 вокруг оси Oz. Эллипсоид (3) называют эллипсоидом вращения.
вокруг оси Oz. Эллипсоид (3) называют эллипсоидом вращения.
Отметим также, что в случае 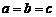 эллипсоид является сферой.
эллипсоид является сферой.
Гиперболоиды.
Однополостным гиперболоидом называется поверхность, которая в декартовой системе координат Oxyz определяется каноническим уравнением
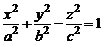 . (1)
. (1)
Установим форму поверхности (1). Для этого рассмотрим сечения ее координатными плоскостями Oxz и Oyz. Получаем соответственно системы уравнений:
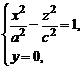
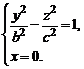 (2)
(2)
 Из (2) следует, что в сечениях будут гиперболы соответственно в плоскостях Oxz и Oyz.
Из (2) следует, что в сечениях будут гиперболы соответственно в плоскостях Oxz и Oyz.
Рассмотрим теперь сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Оху. В сечениях получим линии, определяемые системой уравнений
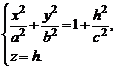 (3)
(3)
Введя величины 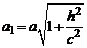 и
и 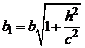 , перепишем систему (3) в виде
, перепишем систему (3) в виде
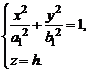 (
( 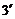 )
)
Из ( 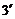 ) заключаем, что плоскость
) заключаем, что плоскость 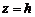 пересекает гиперболоид по эллипсу с полуосями а1 и b1.
пересекает гиперболоид по эллипсу с полуосями а1 и b1.
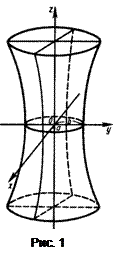
Рассмотренные сечения показывают, что однополостный гиперболоид изображается в виде бесконечной трубки, бесконечно расширяющейся в обе стороны по мере удаления от плоскости Оху (рис. 1).
Величины a, b, c называются полуосями однополостного гиперболоида.
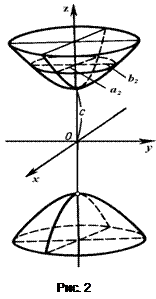
Двуполостным гиперболоидом называют поверхность, определяемую в декартовой системе координат Oxyz каноническим уравнением
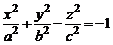 . (4)
. (4)
Для установления формы поверхности (4) рассмотрим сечения этой поверхности координатными плоскостями Oxz и Oyz. Получим соответственно системы уравнений
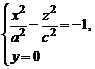 и
и 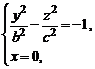
из которых вытекает, что сечения представляются гиперболами. Изучим теперь сечения гиперболоида (1) плоскостями 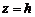 . В сечениях получаем линии
. В сечениях получаем линии
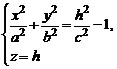 или
или 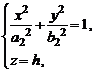 (5)
(5)
 где
где 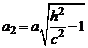 и
и 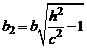 .
.
При 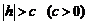 плоскость
плоскость 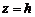 пересекает гиперболоид по эллипсу с полуосями а2 и b2, причем при увеличении
пересекает гиперболоид по эллипсу с полуосями а2 и b2, причем при увеличении 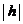 величины а2 и b2 также увеличиваются.
величины а2 и b2 также увеличиваются.
Если 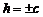 , то из системы (5) получаем только две точки: (0;0;+с) и
, то из системы (5) получаем только две точки: (0;0;+с) и 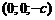 , и поэтому плоскости
, и поэтому плоскости 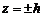 касаются данной поверхности.
касаются данной поверхности.
При 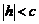 система (5) определяет мнимый эллипс, т.е. плоскость
система (5) определяет мнимый эллипс, т.е. плоскость 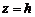 не пересекается с гиперболоидом (4).
не пересекается с гиперболоидом (4).
Рассмотренные сечения позволяют изобразить двуполостный гиперболоид в виде поверхности, состоящей из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши (рис. 2).
Величины a, b, c называют полуосями двуполостного гиперболоида. Если полуоси 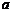 и
и 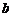 гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси
гиперболоида (однополостного или двуполостного) равны, то он называется гиперболоидом вращения и получается вращением вокруг оси 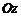 гиперболы
гиперболы 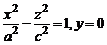 в случае однополостного гиперболоида и гиперболы
в случае однополостного гиперболоида и гиперболы 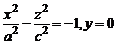 в случае двуполостного гиперболоида.
в случае двуполостного гиперболоида.
Параболоиды.
Эллиптическим параболоидом (рис. 1) называется поверхность, определяемая в декартовой системе координат Oxyz каноническим уравнением
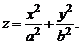 (1)
(1)
Гиперболическим параболоидом (рис. 2) называется поверхность, определяемая каноническим уравнением
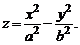 (2)
(2)
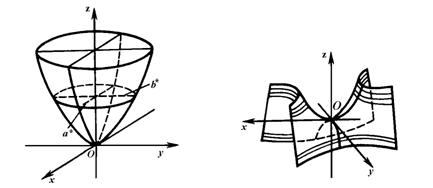
Рис. 1. Рис. 2.
Из уравнений (1) и (2) вытекает, что плоскости Oxz и Oyz являются плоскостями симметрии параболоидов.
Ось Oz называется осью параболоида, а точка ее пересечения с поверхностью параболоида – вершиной.
Оба параболоида плоскостями, параллельными координатным плоскостям Oxz и Oyz, пересекаются по параболам. Например, плоскость 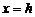 пересекает эллиптический параболоид по параболе
пересекает эллиптический параболоид по параболе
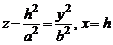 .
.
Из уравнения (1) заключаем, что плоскость 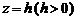 , параллельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу
, параллельная плоскости Oxу, пересекает эллиптический параболоид по эллипсу
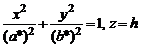 ,
,
где 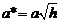 и
и 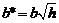 . Из уравнения (2) получаем, что плоскость
. Из уравнения (2) получаем, что плоскость 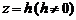 пересекает гиперболический параболоид по гиперболе
пересекает гиперболический параболоид по гиперболе
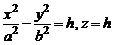 .
.
Плоскость Оху пересекает гиперболический параболоид по двум пересекающимся прямым
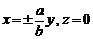 .
.
При 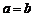 эллиптический параболоид, заданный уравнением
эллиптический параболоид, заданный уравнением
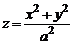 ,
,
называется параболоидом вращения. Он получается при вращении параболы 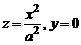 вокруг оси Oz.
вокруг оси Oz.
25. Линейное векторное пространство. Подпространство. Линейная зависимость и независимость векторов линейного пространства. Базис и размерность линейного пространства. Координаты векторов. Преобразование координат вектора при замене базиса.
251. Линейное векторное пространство.
Рассмотрим множество  элементов
элементов 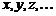 и множество
и множество 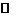 действительных чисел. На элементах этих множеств определим операцию сложения (внутреннюю операцию): каждым двум элементам
действительных чисел. На элементах этих множеств определим операцию сложения (внутреннюю операцию): каждым двум элементам 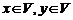 поставим в соответствии третий элемент
поставим в соответствии третий элемент 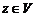 , называемый их суммой
, называемый их суммой 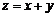 , и операцию умножения на действительные числа (внешнюю операцию): каждому элементу
, и операцию умножения на действительные числа (внешнюю операцию): каждому элементу 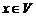 и
и 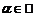 поставим в соответствие элемент
поставим в соответствие элемент 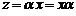 , где
, где 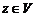 . Потребуем, чтобы для любых элементов
. Потребуем, чтобы для любых элементов 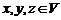 и чисел
и чисел 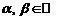 были выполнены следующие аксиомы:
были выполнены следующие аксиомы:
1. 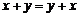 – коммутативный закон.
– коммутативный закон.
2. 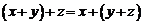 – ассоциативный закон.
– ассоциативный закон.
3. Существует такой элемент 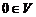 (называемый нулевым элементом), что
(называемый нулевым элементом), что 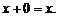
4. Для каждого элемента 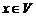 существует такой элемент
существует такой элемент 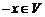 (называемый элементом, противоположным элементу
(называемый элементом, противоположным элементу 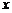 ), что
), что 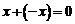 .
.
5. Существует элемент 1, называемый единичным, такой, что 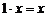 .
.
6. 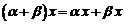 .
.
7. 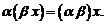
8. 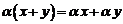 .
.
Множество 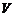 , в котором определены операции сложения элементов и умножения элемента на действительное число, удовлетворяющие аксиомам 1 – 8, называется действительным (вещественным) линейным пространством или действительным (вещественным) векторным пространством, а его элементы называются векторами.
, в котором определены операции сложения элементов и умножения элемента на действительное число, удовлетворяющие аксиомам 1 – 8, называется действительным (вещественным) линейным пространством или действительным (вещественным) векторным пространством, а его элементы называются векторами.
Отметим, что сумму 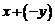 обозначают
обозначают 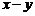 и называют разностью элементов
и называют разностью элементов 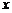 и
и 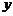 .
.
Примеры линейных пространств.
1.Множество всех свободных векторов 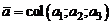 , где
, где 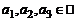 , для которых определены сложение и умножение вектора на число, является линейным пространством
, для которых определены сложение и умножение вектора на число, является линейным пространством 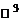 . В этом пространстве роль нулевого элемента играет нулевой вектор
. В этом пространстве роль нулевого элемента играет нулевой вектор 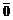 ; противоположным вектору
; противоположным вектору 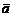 является вектор
является вектор 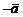 .
.
2.Линейное пространство образует также множество всех матриц  заданного порядка
заданного порядка 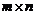 , для которых определены операции сложения и умножения на число. Здесь роль нулевого элемента играет нулевая матрица, а противоположной к матрице
, для которых определены операции сложения и умножения на число. Здесь роль нулевого элемента играет нулевая матрица, а противоположной к матрице 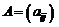
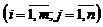 будет матрица
будет матрица 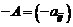
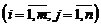 .
.
3. Множество алгебраических многочленов от одной переменной степени не выше n. Нулевой вектор есть многочлен с коэффициентами, равными нулю.
4. множество всех матриц-столбцов длины n.
252. Подпространство.
Пусть задано множество 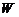 , в котором определены те же операции, что и в линейном пространстве
, в котором определены те же операции, что и в линейном пространстве 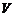 . Множество
. Множество 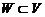 назовем подпространством линейного пространства
назовем подпространством линейного пространства 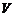 , если выполнены следующие условия: 1) если
, если выполнены следующие условия: 1) если 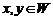 , то
, то 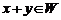 ; 2) если
; 2) если 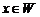 , то
, то 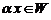 .
.
Очевидно, что всякое подпространство 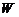 линейного пространства
линейного пространства 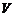 является линейным пространством. В
является линейным пространством. В 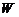 есть нулевой элемент 0: если
есть нулевой элемент 0: если 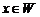 , то
, то 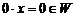 . Для любого элемента
. Для любого элемента 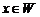 имеется противоположный элемент
имеется противоположный элемент 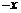 : если
: если 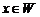 , то
, то 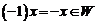 . Отметим, что нулевой элемент 0 линейного пространства
. Отметим, что нулевой элемент 0 линейного пространства 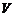 образует подпространство данного пространства V, а само пространство
образует подпространство данного пространства V, а само пространство 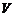 можно рассматривать как подпространство этого пространства. Такие подпространства называют тривиальными, а все другие, если они имеются, нетривиальными.
можно рассматривать как подпространство этого пространства. Такие подпространства называют тривиальными, а все другие, если они имеются, нетривиальными.
Например, множество 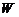 всех свободных векторов
всех свободных векторов 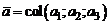 , параллельных некоторой плоскости, для которых определены операции сложения и умножения вектора на число, является подпространством линейного пространства.
, параллельных некоторой плоскости, для которых определены операции сложения и умножения вектора на число, является подпространством линейного пространства.
253. Линейная зависимость и независимость векторов линейного пространства.
Пусть 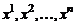 - элементы линейного пространства, а
- элементы линейного пространства, а 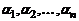 – вещественные числа.
– вещественные числа.
Вектор 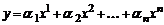 назовем линейной комбинацией векторов
назовем линейной комбинацией векторов 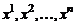 . Если все
. Если все 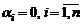 , то линейная комбинация называется тривиальной; если хотя бы одно из чисел
, то линейная комбинация называется тривиальной; если хотя бы одно из чисел 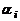 отлично от нуля, то линейная комбинация называется нетривиальной.
отлично от нуля, то линейная комбинация называется нетривиальной.
Система векторов 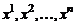 называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е.
называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е.
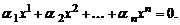 (1)
(1)
Если равенство (1) выполняется только в случае 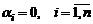 , то система векторов
, то система векторов 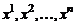 называется линейно независимой.
называется линейно независимой.
Введем понятия коллинеарности и компланарности векторов линейного пространства.
Два вектора 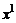 и
и 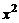 назовем коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора
назовем коллинеарными, если они линейно зависимы, и неколлинеарными, если они линейно независимы. Три вектора 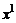 ,
, 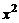 ,
, 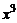 называются компланарными, если они линейно зависимы, и некомпланарными, если линейно независимы.
называются компланарными, если они линейно зависимы, и некомпланарными, если линейно независимы.
254. Базис и размерность линейного пространства.
Линейное пространство называется конечномерным, если существует такое натуральное число n, что в этом пространстве найдетсясистемаиз n линейно независимых векторов, а любая система из (n+1) вектора является линейно зависимой. Число n в этом случае называется размерностью пространства.
Базисом 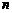 -мерного линейного пространства
-мерного линейного пространства 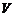 называется любая упорядоченная система
называется любая упорядоченная система 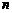 линейно независимых векторов этого пространства. Например, базис пространства
линейно независимых векторов этого пространства. Например, базис пространства 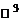 образует любая упорядоченная тройка некомпланарных векторов этого пространства.
образует любая упорядоченная тройка некомпланарных векторов этого пространства.
Система 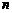 векторов
векторов 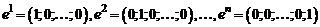 есть базис пространства
есть базис пространства  .
.
255. Координаты векторов.
Теорема 1. Пусть 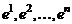 - некоторый базис линейного
- некоторый базис линейного
 -мерного пространства
-мерного пространства 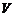 . Тогда любой вектор
. Тогда любой вектор 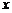 этого пространства линейно выражается через базисные векторы
этого пространства линейно выражается через базисные векторы 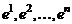 , т.е.
, т.е.
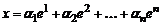 , (5)
, (5)
причем коэффициенты 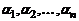 в разложении (5) определяются однозначно.
в разложении (5) определяются однозначно.
Выражение (5) называется разложением вектора 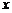 по базису
по базису 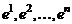 , а коэффициенты
, а коэффициенты 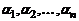 – координатами вектора
– координатами вектора 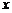 в базисе
в базисе 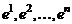 . Если вектор
. Если вектор 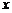 в некотором базисе имеет координаты
в некотором базисе имеет координаты 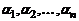 , то записывают
, то записывают 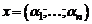 .
.
256. Преобразование координат вектора при замене базиса.
Координаты вектора определяются выбором базиса, а значит, координаты одного и того же вектора будут различными в разных базисах. Формулами преобразования координат называются формулы, которые связывают координаты вектора в разных базисах.
Пусть в 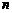 -мерном линейном пространстве
-мерном линейном пространстве 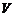 заданы два различных базиса
заданы два различных базиса 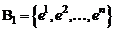 и
и 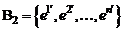 . Матрицей перехода от базиса
. Матрицей перехода от базиса 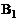 к базису
к базису 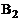 называется матрица системы векторов
называется матрица системы векторов 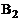 в базисе
в базисе 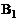 . Векторы из
. Векторы из 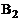 единственным образом можно разложить по базису
единственным образом можно разложить по базису 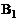 :
:
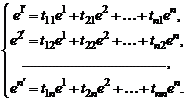 (1)
(1)
Тогда матрица перехода 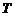 от базиса
от базиса 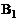 к базису
к базису 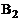 имеет вид:
имеет вид:
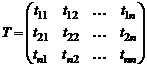 . (2)
. (2)
Возьмем произвольный вектор 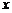 из
из 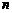 -мерного линейного пространства
-мерного линейного пространства 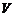 и рассмотрим его координаты
и рассмотрим его координаты 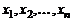 и
и 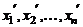 соответственно в базисах
соответственно в базисах 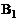 и
и 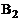 .
.
Формула
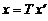 . (3)
. (3)
выражает старые координаты 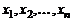 вектора
вектора 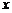 через его новые координаты и называются формулой преобразования координат при переходе от базиса
через его новые координаты и называются формулой преобразования координат при переходе от базиса 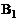 к базису
к базису 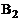 в векторной форме.
в векторной форме.
Умножим полученное равенство слева на 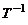 , получим:
, получим:
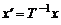 . (4)
. (4)
Равенство (4) определяет преобразование координат при переходе от базиса 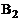 к базису
к базису 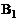 .
.
