Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Формулы Крамера.

5¹. Системы линейных алгебраических уравнений.

Системой m линейных алгебраических уравнений с 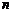неизвестными называется система вида

(1)

Числа , называются коэффициентами системы, а числа , , – свободными членами.

Если все , , то система называется однородной; если хотя бы один из свободных членов ненулевой, то система (1) называется неоднородной.

Решением системы (1) называется любая упорядоченная совокупность 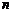чисел , которая при подстановке в каждое уравнение системы (1) на место соответствующих неизвестных, обращает его в тождество. Система (1) называется совместной, если она имеет хотя бы одно решение, в противном случае – несовместной. Совместная система, имеющая только одно решение (больше, чем одно решение), называется определенной (неопределенной).

Систему (1) можно записать в матричном виде: ,

где − матрица системы,

− матрица-столбец неизвестных;

− матрица-столбец свободных членов.

Используя матрицы-столбцы коэффициентов системы (1), ее можно записать также в виде:

.

Две системы называют эквивалентными или равнозначными, если они имеют одно и то же множество решений. Считаем, что всякие две несовместные системы с одинаковым числом неизвестных – эквивалентны.

Элементарными преобразованиями линейной системы называются следующие:

1) умножение уравнения системы на ненулевое число;

2) прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число;

3) перестановка местами двух уравнений системы;

4) вычеркивание уравнения, все коэффициенты которого равны нулю.

Утверждение 1. Применение элементарных преобразований приводит к эквивалентной системе.

Матрица называется расширенной матрицей системы (1).

5². Теорема 1 (Кронекера-Капелли). Для совместности системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.

Следствие 1.Если ранг матрицы системы меньше ранга ее расширенной матрицы, то система несовместна.

Rank (А/b) = rankА

Пример 1. Исследовать на совместность систему

Решение. .

Имеем . Система несовместна, так как rank А не равен матрице расширенной.

5³. Формулы Крамера.

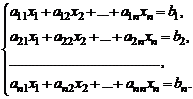(1)

Определителем системы назовем определитель ее матрицы.

Пусть в этом случае система (1) называется невырожденной и ее решение можно найти по формуле

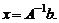(2)

В формуле (2) заключается метод обратной матрицы решения невырожденной системы вида (1).

Из формулы (2) для нахождения решения системы (1) выводятся формулы Крамера

,

где – определитель, который получается из определителя системы D путем замены j-го столбца на столбец свободных членов.

D – опред. системы

Метод Гаусса.

Распространенным точным методом решения систем линейных алгебраических уравнений является метод Гаусса, который применяется для решения произвольных систем линейных алгебраических уравнений. Суть метода состоит в том, что посредством элементарных преобразований система линейных алгебраических уравнений приводится к треугольной или трапециевидной форме (прямой ход метода Гаусса), при помощи которой непосредственно получаются все решения системы (обратный ход метода Гаусса).

На практике прямой ход метода Гаусса как правило применяется не к системе уравнений, а к ее расширенной матрице 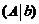и формализуется следующим образом:

А). Рассмотрим элемент, стоящий в первой строке и в первом столбце матрицы 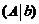. Если этот элемент оказался равным нулю, то переставляем строки матрицы таким образом, чтобы в первой строке, в первом столбце оказался ненулевой элемент. Обозначим этот элемент через 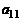и назовем его разрешающим на первом шаге. Пересчитаем элементы матрицы по следующим правилам:

1) строку, в которой стоит разрешающий элемент, назовем разрешающей; столбец, в котором стоит разрешающий элемент − разрешающим;

2) элементы разрешающей строки и всех вышерасположенных строк (на первом шаге только элементы разрешающей строки) остаются неизменными;

3) элементы разрешающего столбца, расположенные ниже разрешающего элемента, обращаются в нули;

4) все остальные элементы матрицы вычисляются согласно следующему правилу прямоугольника. Из четырех элементов матрицы составляется прямоугольник таким образом, что разрешающий элемент и элемент, который пересчитывается, образуют главную диагональ этого прямоугольника. Новое значение пересчитываемого элемента вычисляется как разность произведений элементов главной и побочной диагоналей.

Б) В полученной таблице рассмотрим элемент, стоящий во второй строке и втором столбце. Обозначим его через 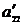. Будем считать, что выполняется неравенство 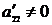. В противном случае вторую строку меняем местами со строкой, имеющей больший номер, таким образом, чтобы во второй строке, втором столбце оказался ненулевой элемент. Если во втором столбце и рассматриваемых строках не нашлось ненулевого элемента, то переставляем местами второй столбец и столбец с большим номером таким образом, чтобы элемент, стоящий во второй строке, втором столбце, не был равен нулю. Теперь назовем элемент 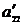− разрешающим на этом шаге и пересчитаем элементы матрицы по правилам 1)-4).

В) Применяем правила 1)-4), двигаясь по строкам матрицы вниз, выбирая в качестве разрешающего элемента ненулевой элемент, стоящий на пересечении стоки и столбца с номерами, совпадающими с номером шага. Если в процессе преобразований образуется строка, состоящая из нулей, то эту строку удаляем.

Для выполнения обратного хода метода Гаусса возвращаемся от преобразованной матрицы системы к системе уравнений. При этом, если в процессе прямого хода метода производилась перестановка столбцов, то в системе, соответствующей преобразованной матрице, должно быть выполнено соответствующее переименование переменных.

Если в полученной системе встретится уравнение вида 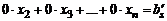, где 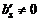, то исходная система несовместна. В противном случае − совместна.

Совместная система после преобразований имеет вид:

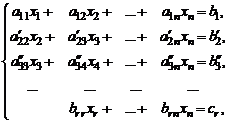(1)

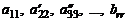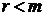где коэффициенты отличны от нуля. Для произвольной системы справедливы неравенства . Неравенство выполняется в тех случаях, когда в процессе прямого хода метода удалялись нулевые строки (т.е. удалялись уравнения вида .)

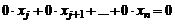В процессе обратного хода метода Гаусса находятся все решения системы. Если в системе (1) 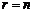, то она имеет треугольный вид. Из последнего уравнения 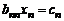находим 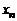_, из предпоследнего – 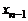и т.д. и, наконец, из первого – 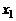,и, тем самым, – единственное решение исходной системы.

Если 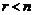, то в результате обратного хода r неизвестных можно выразить линейно через остальные 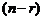неизвестных. Эти r неизвестных называют базисными, а остальные 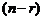– свободными. В результате получим общее решение системы в виде:

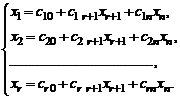(5)

Чтобы получить какое-нибудь частное решение исходной системы, нужно придать свободным неизвестным некоторые числовые значения. Ясно, что в случае r < п система имеет бесконечное множество решений.