Независимость аксиоматической системы.

Непротиворечивая система аксиом называется независимой, если ни одна из аксиом этой системы не может быть выведена (или опровергнута) из остальных аксиом как теорема. В противном случае система аксиом называется зависимой.

Для иллюстрации этого свойства обратимся снова к геометрической теории, основанной на аксиоматике Гильберта. Ясно, что непосредственная проверка независимости каждой из 20 аксиом затруднительна. История V постулата "Начал" Евклида является поучительным тому примером. Четвертый постулат о конгруэнтности всех прямых углов в последствии был доказан как логическое следствие других аксиом и постулатов (точнее других "очевидных" утверждений). Возник вопрос о независимости или прямом доказательстве следующего, пятого постулата о параллельных прямых. Тем более, см. замечание к аксиоме параллельности в §2 , что как бы "половина доказательства" аксиомы параллельности уже была известна. Более двух тысяч лет предпринимались попытки доказать одно из двух: либо то, что V постулат есть логическое следствие других "более очевидных" утверждений, либо то, что он не доказывается исходя из каких-либо "очевидных" утверждений, аксиом и постулатов.

Сформулируем назревший вопрос. Существует ли эффективное достаточное условие для проверки независимости какого-либо утверждения А от системы аксиом Т (проверенной уже на совместность). Такое условие существует и для совместной системы аксиом формируется следующим образом в терминах реализаций.

Теорема. Пусть Т – непротиворечивая система аксиом. Утверждение А не зависит от системы аксиом Т, если вместе с некоторой реализацией R₁ (Т , А) системы Т и утверждения А существует некоторая другая реализация R₂(T, ùА ) системы Т и отрицания утверждения ùА.

Доказательство. Пусть существует реализация R₂(T, ùA) системы аксиом Т и отрицания утверждения - ùА, и пусть Т 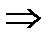А. Тогда реализация R₂(T, ùA) содержит вместе со свойством ùА и его отрицание А=ù (ùА), что несовместимо с понятием реализации (см. п.6.3, §6, если в реализации выполняется некоторое свойство, то не может выполнятся одновременно и его отрицание). Следовательно, предположение Т 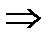А (о том, что А следует из Т) неверно. Точно так же можно проверить, что наличие реализации R₁(Т ,А) не позволяет опровергнуть утверждение А. Действительно, пусть Т 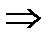˥А, то есть, имеет место опровержение утверждения А. Тогда реализация R₁(Т , А) вместе со свойством А обладает и свойством ùА, что невозможно по определению реализации. Теорема доказана.

В качестве применения этого достаточного условия докажем независимость аксиомы параллельности от всех остальных 14 аксиом планиметрии.