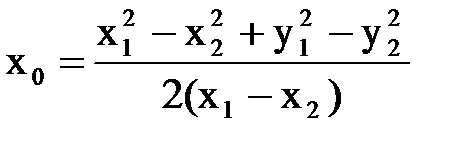1. Точками плоскости Лобачевского будем называть все точки одной из полуплоскостей, например, верхней, лежащих по одну сторону от l.
2. Прямыми плоскости Лобачевского назовем либо вертикальные лучи, лежащие в заданной полуплоскости, либо полуокружности с центрами на l, также лежащими в этой полуплоскости, рис.5.1.
3.Прямая l представляет «бесконечно удаленные точки» плоскости Лобачевского и называется абсолютом (абсолют можно рассматривать как параметризацию направлений прямых).
4.Углы между прямыми - это обычные евклидовы углы, образованные касательными в точке пересечения полуокружностей, представляющих эти «прямые», рис. 1.
5. Движение в модели Пуанкаре плоскости Лобачевского представляется специальными дробно-линейными преобразованиями верхней полуплоскости на себя. Это преобразование сохраняет отношение 4-х точек, через которое определяется функция расстояния между двумя точками в модели Пуанкаре. Мы не будем иллюстрировать свойства конгруэнтности на плоскости Лобачевского, поэтому не приводим свойства дробно-линейных отображений и формулы, представляющие функцию расстояния. Подробно изложение свойств движения в модели Пуанкаре плоскости Лобачевского можно так же найти в интернете по ключевым словам «движения в модели Пуанкаре плоскости Лобачевского».
В модели, определяемой перечисленными выше условиями 1-5, выполняются все 15 аксиом планиметрии Лобачевского. Эту модель будем обозначать L2 и ограничимся проверкой нескольких аксиом.
Проверим две первые аксиомы I группы. Они должны определять единственную прямую в модели L2 по двум любым точкам. Пусть абсолют l - линия OX в евклидовой плоскости. Тогда уравнения окружностей с центром в точках A(x0, О) Î l и радиусом R имеют вид:
(x-x0)2 + y2 = R2 (5.1)
Две точки B(x1,y1), C(x2,y2) лежат на некоторой «прямой» a тогда и только тогда, когда их координаты удовлетворяют уравнению (5.1) для некоторых значений x0 и R:
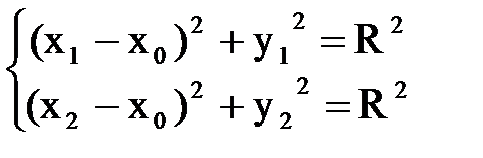 (5.2)
(5.2)
В полученной алгебраической системе уравнений числа x1, y1 и x2, y2 заданы, а величины x0 и R - искомые. Раскрывая квадраты и вычитая второе уравнение из первого, находим
x12 – x22 + y12 – y22 = 2x0(x1 – x2).
Откуда
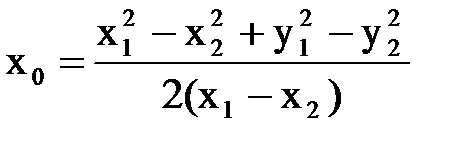
Это решение определено, если x1¹x2, т.е. точки B и C не лежат на общем перпендикуляре x1=x2=х к оси OX. (Если x1=x2=x, то этот перпендикуляр представляет прямую в L2, рис. 5.2(a)). Подставляя найденное значение x0, в любое из уравнений (5.2), находим значение радиуса R. Тем самым найдена «прямая» моделируемая полуокружностью (5.1), проходящей через точки B и C. Эта окружность единственна и в модели L2 представляет единственную же «прямую» a, инцидентную точкам B и C, рис. 5.2.
Таким образом, аксиомы 1 и 2 группы I выполнены. Аксиома 3 этой группы выполняется очевидным образом.
Оставляя проверку аксиом группы II-IV, займемся проверкой аксиомы V' (параллельности по Лобачевскому) в модели L
2. Пусть a - некоторая прямая и точка AÏa в модели L
2, рис.5.3. Пусть A
¥ и B
¥ - точки на абсолюте l, представляющие бесконечно удаленные точки прямой a, рис.5.3. Используя формулу (5.1) точно так же, как при проверке аксиом 1-2 группы I, заключаем, что существует единственная окружность с центром на l, проходящая через точки A и A
¥, обозначим ее g
1(A,A
¥), и, аналогично, единственная окружность g
2(A,B
¥), рис.5.3. Полуокружности g
1 и g
2 в верхней полуплоскости L
2 моделируют две прямые, параллельные прямой a, т.к. имеют с ней общие точки A
¥=g
1Ça и B
¥=g
2Ça, лежащие на абсолюте l и являющиеся, по определению, бесконечно удаленными точками. Кроме этого, существует еще бесконечно много прямых g, представляемых окружностями, проходящими через точку A внутри вертикального угла, образованного g
1, и g
2, рис 5.3. Эти прямые не имеют общих точек с a в L
2 даже на абсолюте и называются прямыми, расходящимися с a.
Следствие 1.
В плоскости L2 через точку A вне прямой a проходит бесконечное множество прямых, не имеющих общих точек с a (расходящихся с a). При этом существует в точности две параллельные g1 и g2, имеющие общие точки с a на абсолюте l:
A¥ = g1 Ç aÎ l, A¥ = g2 Ç aÎ l,
Вывод.
В модели L2 выполняются 15 аксиом планиметрии Лобачевского.
5.2 Основные неевклидовы факты в планиметрии Лобачевского.
Принятие столь экзотической аксиомы параллельности V' позволяет «обнаружить» (точнее, строго доказать) на плоскости L2 неевклидовы «эффекты», т.е. такие отношения между геометрическими объектами, которые не реализуются в евклидовой плоскости.
Ограничимся иллюстрацией ряда свойств взаимного расположения прямых на плоскости L2. Строгое доказательство этих фактов можно найти, например, в [ ].
1. Сумма углов многоугольника в плоскости L2.
Рассмотрим треугольник, рис. 5.4(а) с вершинами, лежащими на абсолюте. Т.к., по определению абсолюта вершины, А
1,А
2,А
3 - бесконечно удалены, то этот треугольник образован тремя прямыми - сторонами А
1А
2, А
1А
3 и А
2А
3 бесконечной длины. Т.к. в вершинах А
1, А
2 и А
3 окружности касаются друг друга, то представляемые ими «прямые» А
1А
2, А
1А
3 и А
2А
3 образуют нулевые углы между собой. Аналогично, на рис. 5.4(б) представлен n-угольник с бесконечно длинными сторонами и суммой углов, равной нулю.
Если внутренние окружности на рис. 5.4(a) и (б) взять чуть большего радиуса, то точки А1А2…Аn попадут в плоскость L2 (не будут лежать на абсолюте), перестанут считаться бесконечно удаленными. Тогда длины сторон многоугольника станут конечными, а сумма углов многоугольника станет несколько больше нуля. С другой стороны, если треугольник образован «малыми» кусками дуг окружностей, рис.5.5, то сумма его углов приближается к 180°, но остается все же несколько меньше 180°.
Следствие 2.
В плоскости Лобачевского L2 сумма углов треугольника не постоянна и может принимать любое значение больше нуля и меньше p.
2. Взаимное расположение прямых в плоскости L2.
Всякие две прямые в плоскости L2 либо пересекаются, либо параллельны, либо являются расходящимися, т.е. не параллельны и не пересекаются, рис. 3.
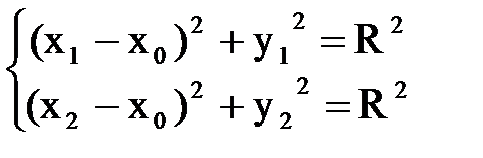 (5.2)
(5.2)