Основные теоремы дифференциального исчисления. Теорема Коши.

Теорема 3. (Теорема Коши) Пусть функции f(x) и g(x)непрерывны на отрезке [a, b];дифференцируемы в интервале (a, b);

"x О (a, b) g'(x) ≠ 0 .

Тогда существует точка c О (a, b) так-g(a) = f’(c)/g’(c)
Доказательство:

Пусть 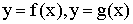- гладкие на .

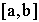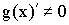на

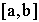
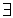
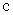
Тогда 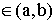: 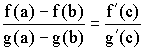, где .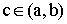

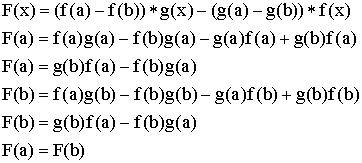
F – гладкая на отрезке 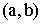. По теореме Ролля : .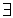

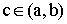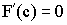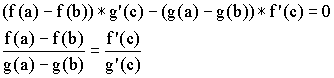
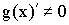по условию, а 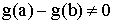так как иначе по теореме Ролля 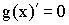, что противоречит условию.

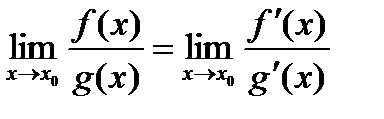24. Правило Лопиталяпредлагает эффективный способ раскрытия неопределенносте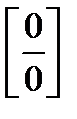й и .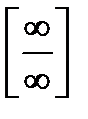
Теорема. Предел отношения двух дифференцируемых бесконечно малых или бесконечно больших функций равен пределу отношения их производных (если он существует, конечен или бесконечен):

.

Пример1. .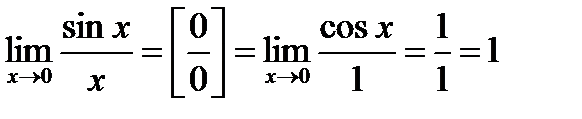

Пример 2. .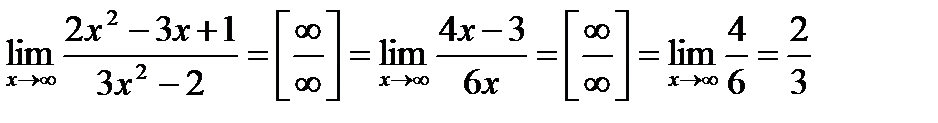

Пример 3. .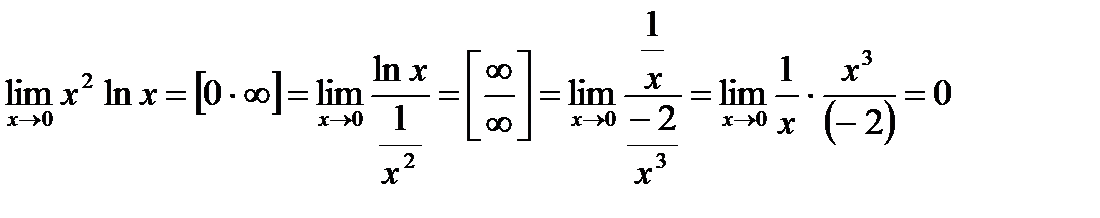

Пример 4. .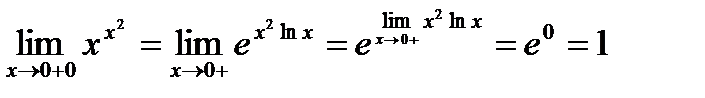

25. Возрастание и убывание функций одной переменной.
Определение. Функция f(x) называется возрастающей на интервале (a,b) , если для любых точек x1,x2 из этого интервала при выполнении условия x1<x2 выполняется неравенство f(x1)<f(x2) (большему значению аргумента соответствует большее значение функции).
Возрастающие на интервале (a,b) и убывающие на интервале (a,b) функции называются монотонными на интервале (a,b) .
Знание производной дифференцируемой функции позволяет находить интервалы ее монотонности.
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой на интервале (a,b) функции f(x) положительна на интервале (a,b) , то функция f(x) монотонно возрастает на этом интервале.
Доказательство. Зафиксируем любые точки x1,x2 на интервале (a,b) такие, что x1<x2 .
Тогда по следствию из теоремы Лагранжаf(x2)-f(ε )(x1)=f(x2-x1) , где x1< ε<x2 . По условию на всем интервале (a,b) f(x)>0 , то естьf(ε)>0 , следовательно,f(x2)-f(x1)>0 . Таким образом, f(x) действительно возрастает на (a,b) , что и требовалось доказать.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой на интервале (a,b) функции f(x) отрицательна на интервале (a,b) , то функция f(x) монотонно убывает на этом интервале.

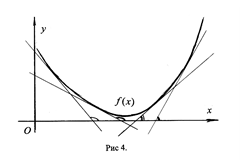
Геометрический смысл этих теорем состоит в том, что на интервалах убывания функции касательные к графику функции образуют с осью Ox тупые углы, а на интервалах возрастания – острые.

Максимум и минимум функции

Пусть функция z=f(x;y) определена в некоторой области D иM0(x0;y0)ÎD
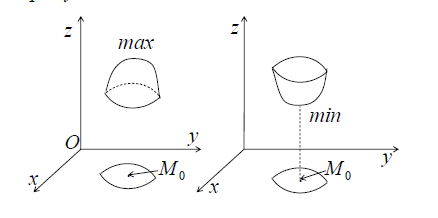
Опр.1 ТочкаM0(x0;y0) называется точкой максимумафункции z=f(x;y), если существует такая δ-окрестностьэтой точки, что для каждой точки M¹M0из этойокрестности выполняется неравенство: f(x;y) <f(x0;y0)
Опр.2 Точка M0(x0;y0) называется точкой минимумафункции z=f(x;y), если существует такая δ-окрестностьэтой точки, что для каждой точки M¹M0из этойокрестности выполняется неравенство: f(x;y) >f(x0;y0)
Значение функции z=f(x;y) в точке максимума(минимума) называется максимумом (минимумом)функции. Максимум и минимум функции называют ееэкстремумами.
Замечание1: В силу определения, точка экстремумалежит внутри области определения функции.Максимум и минимум имеют локальный (местный)характер: значение функции в точкеM0(x0;y0)сравнивается с ее значениями в точках, достаточноблизких к (x0;y0)
В области D функция может иметь несколько экстремумов или не иметь ни одного.

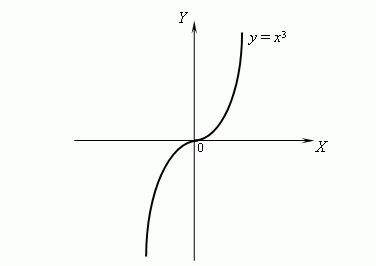27. Выпуклость и вогнутость кривой. Точки перегиба.
Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в точке ( x0 ), и обозначается f '' ( x0 ).
Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 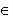( a, b ).
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 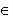( a, b ).
Достаточное условие вогнутости ( выпуклости )функции.Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:если f '' ( x ) > 0 для любого x 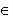( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x 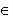( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
Рассмотрим график функции y = x3

Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x> 0 при x > 0 и 6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3.

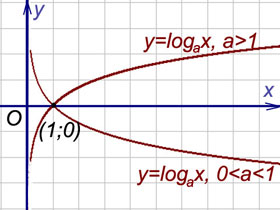28. Асимптоты графика функций

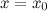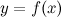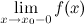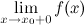Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно 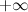или .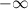

Замечание. Прямая 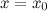не может быть вертикальной асимптотой, если функция непрерывна в точке 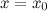. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

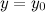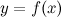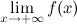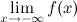Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно 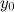.