Теоремы о непрерывных функциях.

Теорема 1. Если функции f(x) и g(x) непрерывны в точке х₀, то в этой точке непрерывны f(x) ± g(x), f(x) · g(x), f(x)/g(x)

(g(x₀) ≠ 0).

Теорема 2. Если функция u(x) непрерывна в точке х₀, а функция f(u) непрерывна в соответствующей точке u₀ = f(x₀), то сложная функция f(u(x)) непрерывна в точке х₀.

Теорема 3 (ограниченность непрерывной функции). Если функция f(x) непрерывна в точке x₀, то существует окрестность O(x₀), в которой f(x) ограничена.

Теорема 4 (устойчивость знака непрерывной функции). Если функция f(x) непрерывна в точке x₀ и f(x₀) ≠ 0, то существует окрестность точки x₀, в которой f(x) ≠ 0, причем знак f(x) в этой окрестности совпадает со знаком f(x₀).

33. Свойства непрерывных функций.

1)Первая теорема Вейерштрасса

Если ф-ция f(x) непрерывна на отрезке [а, b], то она ограничена на этом отрезке.

Теорема неверна, если в ней отрезок заменить интервалом (а,b) или полуинтервалом[a,b) либо (a,b]

2) Вторая теорема Вейерштрасса

Если ф-ция f(x)прерывна на отрезке [a, b], то она достигает на этом отрезке своего наименьшего значения m и наиб. Значения М, т.е. сущ-ют точки 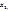, 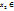[a, b], такие, что f( )=m, f(

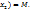
Теорема утверж-т, что знач-я непрерыв.на отрезке [а, b] ф-ции заключены между ее наибольшими и наимен. знач-ями, т.е. m ≤ f(x) ≤M x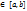

3) Теорема Больцано-Коши о промежут.значении

Если ф-ция f(x) непрерывна на отрезке [a, b]и f(a)=A, f(b)=B (A≠B), то каково бы ни было число С, заключенное между А и В, найдется точка z 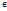[a, b], такая, что f(z)=C.

Cледствие. Если ф-ция f(x) непрерывна на отрезке [a, b] и на его концах принимает знач-я разных знаков, то на этом отрезке сущ-ет хотя бы одна точка 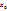, в кот. ф-ция обращается в нуль, т.е.f( 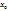)=0

Алгебраич.сумма любого конечного числа непрерыв. на некот. отрезке ф-ций непрерывна на этом отрезке.

34. Производная функции. Геометрический, механический и экономический смысл производной. Эластичность ф-и.

Пусть ф-ция y=f(x) определена на некот множ-тве Х, тогда произв.ф-цией y=f(x) назыв. предел отношения приращения ф-ции к приращению независ. переменной, если этот предел сущ-ет когда приращ-е аргумента стремится к нулю. Если ввести обозначения: 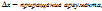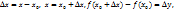то выраж-е можно записать в виде:

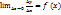Обозначается произ-я у’, f’(x).

C геометр. точки зр. значения производной ф-ции, вычисленное в некот. точке 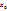численно равно угловому коофициенту касательной, проведенной к графику ф-ции у=f(x) в точке с абсциссой ,

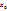т.е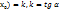. f’( ; f’(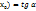

Производная имеет простой механический смысл. Пусть материальная точка движется по оси y.Путь, пройденный этой точкой за время t с учетом направления движения, записывается функцией y=f(t). В течение интервала времени от t₀ до t₀ + 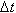,точка перемещается на расстояние: x ( t₀ + 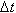) - x ( t₀ ) = .

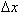v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Ускорение – это производная скорости по времени: a = v’ ( t ). Эластич-тью ф-ции у=f(x) относ-но переменной х назыв-ся предел: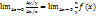

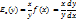
Эластич-ть относ-но х есть приближен.процентн прирост ф-ции (повышение/пониж-е) при приращении независ переменной на 1%. Пусть y(x) — функция, характеризующая, например, издержки производства, где x — кол-во выпускаемой продукции. Тогда отношение 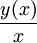описывает средние издержки, приходящиеся на одно изделие. Среднее приращение, средний прирост, средняя скорость изменения определяется отношением 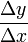. 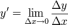выраж пред изд произ-ва. Аналогично рассчит пред доход.

35. Правила дифференцирования. Таблица производных.

; ; ;

; ;

;

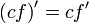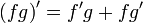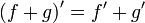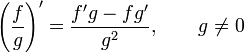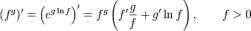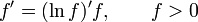36. Производная степенно-показательной и неявной функции. Производные высших порядков.

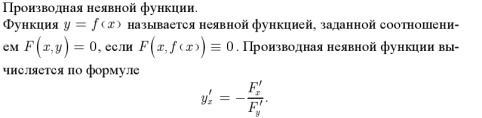
Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f (n)(x) = (f (n -1)(x))' .

37. Теорема Ферма. Теорема Ролля. Их геометр смысл.

Теорема Ферма: Пусть ф-ция y=f(x) определена на некот-ом интервале (a,b) и в точке c принадлеж-ей (a,b) приним-ет наибольш-ее или наимен-шее знач-ие. Если сущ-ет произв-ая f^’(c) , то она рана нулю. Геометрический смысл этой теоремы состоит в том, что в точке экстремума касательная к кривой параллельна оси абсцисс(1)

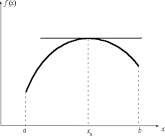(1) (2)

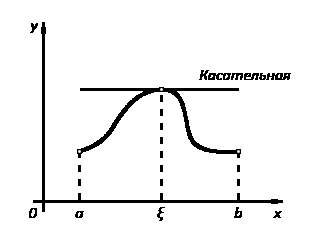
Теорема Ролля: Если функция f(x) непрерывна на заданном промеж/ [a,b] диффер. на интервале (a,b) и f(a)=f(b)(на концах значения равны) то существует т. с из интерв. (a,b), такая, что f’(c)=0.

Геометрический смысл : если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.(2)

38. Теорема Лагранжа, ее геометр смысл. Правило Лопиталя.

Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f(b) - f(a) = (b - a)f '(x).

Правило Лопиталя: испол-ся для нахождения пределов отношения двух бесконечно малых или бесконечно больших ф-ций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞.

Пусть ф-цииf(x) и g(x) дифферен-емы при x>c, 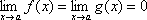и сущ-ет конечный и бесконечный предел 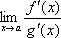где g^’(x) не равно 0 . Тогда сущ-ет и предел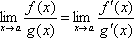

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.