| Примеры плоскостей мы встречаем в жизни постоянно. Это поверхности окна, парты, школьной доски, но в отличие от этих поверхностей математическая плоскость не ограничена краями. Она простирается бесконечно во все стороны. |
 Нарисуем две точки A и B . Проведем через них по линейке линию как на рисунке. У нас получилась прямая, которую обозначают прямая AB или прямая BA . Через любые две точки проходит одна единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки A и B лежат на прямой. Прямая разделяет плоскость на две части, две полуплоскости. Нарисуем две точки A и B . Проведем через них по линейке линию как на рисунке. У нас получилась прямая, которую обозначают прямая AB или прямая BA . Через любые две точки проходит одна единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки A и B лежат на прямой. Прямая разделяет плоскость на две части, две полуплоскости. |
 Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA . Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее. В отличие от прямой луч бесконечен только в одну сторону. Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA . Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее. В отличие от прямой луч бесконечен только в одну сторону. |
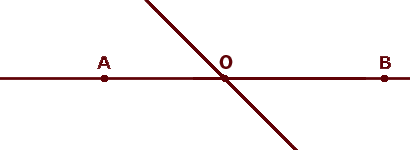 Если две прямые имеют общую точку, например O , как на рисунке, то говорят, что они пересекаются в этой точке. Точка O — точка пересечения прямых. Если две прямые имеют общую точку, например O , как на рисунке, то говорят, что они пересекаются в этой точке. Точка O — точка пересечения прямых. |
Шкалы и координаты. Правила
  Длины измеряют разными измерительными приборами. Один из них — линейка (рис. сверху). Деления, нанесенные на линейку, разбивают ее на равные части. Расстояние между мелкими рисками равно 1 миллиметр, а между крупными 1 сантиметр. Шкалы могут быть и на других измерительных приборах, например термометр (рис. слева). Данный термометр имеет цену деления равную 1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).Наведите курсор на рисунок и подождите. Длины измеряют разными измерительными приборами. Один из них — линейка (рис. сверху). Деления, нанесенные на линейку, разбивают ее на равные части. Расстояние между мелкими рисками равно 1 миллиметр, а между крупными 1 сантиметр. Шкалы могут быть и на других измерительных приборах, например термометр (рис. слева). Данный термометр имеет цену деления равную 1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).Наведите курсор на рисунок и подождите. |
На рисунке внизу изображен луч ОХ. Отметим на этом луче точку F . Под началом луча, точка O , напишем число 0 , а под точкой F — число 1. Отрезок OF называется единичным отрезком. Нанесем на луч точку D , так чтобы расстояние OF было равно расстоянию FD и под точкой D напишем число 2 . Затем на этом же луче отложим отрезок DE , равный единичному отрезку, и под точкой E напишем число 3 . Повторяя эти действия, мы получим бесконечную шкалу. Ее называют координатным лучом. Числа 0, 1, 2, 3, ... , соответствующие точкам O, F, D, E ... , называют координатами этих точек. Пишут: О(0), F(1), D(2), E(3) и т. д.  |
 На рисунке выше изображены кухонные весы, которые используются для измерения массы. Вы видите две шкалы, наведите мышку на рисунок. На первой цена большого деления равна 500 грамм , а меньшего — 100 грамм. На втором рисунке цена большого деления 200 г. , меньшего — 100 г. , а самого маленького 25 г. По подписям делений хорошо видно что, 1000 грамм равны 1 килограмму. 1000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100 кг = 1 ц (центнер); 1000 кг = 1 т (тонна). На рисунке выше изображены кухонные весы, которые используются для измерения массы. Вы видите две шкалы, наведите мышку на рисунок. На первой цена большого деления равна 500 грамм , а меньшего — 100 грамм. На втором рисунке цена большого деления 200 г. , меньшего — 100 г. , а самого маленького 25 г. По подписям делений хорошо видно что, 1000 грамм равны 1 килограмму. 1000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100 кг = 1 ц (центнер); 1000 кг = 1 т (тонна). |
Сравнение чисел. Правила
При счете натуральные числа называют по порядку: 1, 2, 3, 4, ... . Число, которое при счете называют раньше, меньше того, которое при счете называют позже. Число 1 меньше, чем 3, а число 4 больше, чем 3. Единица — самое маленькое натуральное число. Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой. 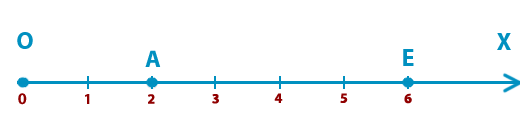 Например, точка A(2) (см. рисунок) лежит левее точки E(6). Нуль меньше любого натурального числа. Например, точка A(2) (см. рисунок) лежит левее точки E(6). Нуль меньше любого натурального числа. |
| Результат сравнения двух чисел записывают в виде неравенства, применяя знаки < (меньше) и > (больше) . Например: 1 < 3 ; 4 > 3 ; 5 < 7 . Число 3 меньше, чем 4, и больше, чем 1. Это записывают в виде двойного неравенства: 1 < 3 < 4 . Так как нуль меньше, чем единица, то записывают: 0 < 1 . |
| Многозначные числа сравнивают так. Число 1007 больше, чем 929, потому что 1007 — четырехзначное число, а 929 — трехзначное. 1007 > 929. Числа 3221 и 1723 — четырехзначные, но 3221 > 1723, потому что в первом числе больше тысяч, чем во втором. В четырехзначных числах 7505 и 7287 поровну тысяч, но сотен в первом числе больше, и потому 7505 > 7287 . |
Знаками < и > обозначают также результат сравнения отрезков.  Если отрезок OA короче отрезка AE, то пишут: OA < AE. Если отрезок OA короче отрезка AE, то пишут: OA < AE. |
 Если же отрезок OA длинее отрезка AE, то пишут: OA > AE . Если же отрезок OA длинее отрезка AE, то пишут: OA > AE . |
| Легкий способ запоминания, когда использовать < , а когда > , для сравнения чисел. Меньшее число должно находиться с острого (маленького) конца знака, а большее с широкого (большого) конца знака: 1 < 3 ; 3 > 1. |
| Сложение и вычитание натуральных чисел |
 6. Сложение натуральных чисел и его свойства 6. Сложение натуральных чисел и его свойства |
 7. Вычитание натуральных чисел и его свойства 7. Вычитание натуральных чисел и его свойства |
 8. Уравнение 8. Уравнение |
Наши рекомендации
 Нарисуем две точки A и B . Проведем через них по линейке линию как на рисунке. У нас получилась прямая, которую обозначают прямая AB или прямая BA . Через любые две точки проходит одна единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки A и B лежат на прямой. Прямая разделяет плоскость на две части, две полуплоскости.
Нарисуем две точки A и B . Проведем через них по линейке линию как на рисунке. У нас получилась прямая, которую обозначают прямая AB или прямая BA . Через любые две точки проходит одна единственная прямая. Прямая не имеет концов. Она неограниченно продолжается в обе стороны. Точки A и B лежат на прямой. Прямая разделяет плоскость на две части, две полуплоскости.  Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA . Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее. В отличие от прямой луч бесконечен только в одну сторону.
Если прямую AB разделить точкой O, то мы получим два луча, которые будут называться луч OB и луч OA . Переставлять буквы в их названиях нельзя, потому что точка O является началом этих лучей, и названия начинаются именно с нее. В отличие от прямой луч бесконечен только в одну сторону.  Если две прямые имеют общую точку, например O , как на рисунке, то говорят, что они пересекаются в этой точке. Точка O — точка пересечения прямых.
Если две прямые имеют общую точку, например O , как на рисунке, то говорят, что они пересекаются в этой точке. Точка O — точка пересечения прямых. 
 Длины измеряют разными измерительными приборами. Один из них — линейка (рис. сверху). Деления, нанесенные на линейку, разбивают ее на равные части. Расстояние между мелкими рисками равно 1 миллиметр, а между крупными 1 сантиметр. Шкалы могут быть и на других измерительных приборах, например термометр (рис. слева). Данный термометр имеет цену деления равную 1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).Наведите курсор на рисунок и подождите.
Длины измеряют разными измерительными приборами. Один из них — линейка (рис. сверху). Деления, нанесенные на линейку, разбивают ее на равные части. Расстояние между мелкими рисками равно 1 миллиметр, а между крупными 1 сантиметр. Шкалы могут быть и на других измерительных приборах, например термометр (рис. слева). Данный термометр имеет цену деления равную 1 градус Цельсия. Сейчас он показывает температуру 18 °C (градусов Цельсия).Наведите курсор на рисунок и подождите. 
 На рисунке выше изображены кухонные весы, которые используются для измерения массы. Вы видите две шкалы, наведите мышку на рисунок. На первой цена большого деления равна 500 грамм , а меньшего — 100 грамм. На втором рисунке цена большого деления 200 г. , меньшего — 100 г. , а самого маленького 25 г. По подписям делений хорошо видно что, 1000 грамм равны 1 килограмму. 1000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100 кг = 1 ц (центнер); 1000 кг = 1 т (тонна).
На рисунке выше изображены кухонные весы, которые используются для измерения массы. Вы видите две шкалы, наведите мышку на рисунок. На первой цена большого деления равна 500 грамм , а меньшего — 100 грамм. На втором рисунке цена большого деления 200 г. , меньшего — 100 г. , а самого маленького 25 г. По подписям делений хорошо видно что, 1000 грамм равны 1 килограмму. 1000 г = 1 кг (килограмм); 1 г = 1000 мг (миллиграмм); 100 кг = 1 ц (центнер); 1000 кг = 1 т (тонна).  Например, точка A(2) (см. рисунок) лежит левее точки E(6). Нуль меньше любого натурального числа.
Например, точка A(2) (см. рисунок) лежит левее точки E(6). Нуль меньше любого натурального числа.  Если отрезок OA короче отрезка AE, то пишут: OA < AE.
Если отрезок OA короче отрезка AE, то пишут: OA < AE.  Если же отрезок OA длинее отрезка AE, то пишут: OA > AE .
Если же отрезок OA длинее отрезка AE, то пишут: OA > AE .  6. Сложение натуральных чисел и его свойства
6. Сложение натуральных чисел и его свойства  7. Вычитание натуральных чисел и его свойства
7. Вычитание натуральных чисел и его свойства  8. Уравнение
8. Уравнение 