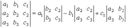Матрицы и действия над матрицами.

Матрицы и действия над матрицами.

Матрица- прямоуг таблица чисел, содерж m-строк и n-столбцов.

1.Матрицы равны между собой, если равны соответств элементы этих матриц.

2.Матрица, в которой m=n наз квадратной или n-ого порядка.

3.Квадратная матрица, у которой все элементы, кроме элементов гл диагонали, равны 0 называется диагональной.

4.Диаг матрица, у которой каждый элемент главной диаг =1 наз единичной.

5.Квадратная матрица наз. треугольной, если все элементы, расположенные по одну сторону её гл диаг =0.

6.Матрица, у которой все числа, стоящие на гл диаг не нулевые, а также некоторое кол ненулевых строк, наз трапециевидной.

7.Матрица, содерж один столбец или строку, наз вектором из Rⁿ пространства.

Действия:

Сложение – только для матриц одинакового размера.

Умножение на число. Множества матриц одинакового размера обознач M^m*n. Тогда введённое на этом мн-ве операции сложения и умнож на число превращ M^m*n в линейное пр-во, векторами которого явл матрицы m*n.

Умножение на вектор-столбец. Для умножения матрицы на вектор-столбец надо, чтобы число столбцов матрицы было равно числу координат вектора.

Две матрицы наз эквивалентными, если одна из них получена из другой с помощью элементарным преобраз. любую матрицу можно привести к канонической.

Определители второго и третьего порядка.
Определителем второго порядка, соответствующим таблице элементов

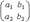
называется число a1 b2 - a2 b1. Определитель второго порядка обозначается так:

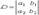
Определитель третьего порядка, соответствующий таблице элементов

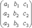
определяется равенством

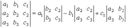
Минор и алгебраическое дополнение.

Минор –это определитель, полученный вычеркиванием строки или столбца. Базисный минор –любой минор r порядка м-ы А отличный от 0. Минором Мij матрицы A, n*n, называется определитель, полученный вычеркиванием i строки и j столбца из матрицы А. Минор, взятый с определенным знаком называется алгебраическим дополнением элемента.A_ij = (-1) ^(i + j) M_ij

Перестановка и транспозиция. Определитель n-го порядка.

Перестановкой n-ого порядка называется любое упорядоченное расположение чисел 1, 2, 3,..., n.

Например, две перестановки второго порядка будут (1,2) и (2,1).

Операция перехода от одной перестановки к другой, при которой два числа меняются местами, а остальные остаются на своих местах, называется транспозицией.

Определителем квадратной матрицы n-ого порядка называется число, равное

алгебраической сумме n членов, каждый из которых является произведением n-

элементов матрицы, взятых по одному из каждой строки или столбца (причём знак каждого члена определяется как (-1)r(j), где r(j)-число инверсий

Ранг матриц.

Максимальное число линейно-зависимых строк матрицы A наз. рангом матрицы и обознач r(a). Наибольшее из порядков миноров данной матрицы отличных от 0 наз рангом матрицы.

Свойства:

1)при транспонировании rang=const.

2)если вычеркнуть нулевой ряд, то rang=const;

3)rang=cost, при элементарных преобразованиях.

3)для вычисл ранга с помощью элементар преобраз матрица A преобраз в матриц B, ранг которой легко находится.

4)ранг треуг матрицы=числу ненулевых элем, располож на глав. диагоналях.

Методы нахождения ранга матрицы:

1. метод окаймляющих миноров

2. метод элементарных преобразований

метод окаймляющих миноров:

метод окаймляющих миноров позволяет алгоритмизировать процесс нахождения ранг-матрицы и позволяет свести к минимуму количество вычисления миноров.

1) если в матрице все нулевые элементы, то ранг = 0

2) если есть хоть один ненулевой элемент => r(a)>0

теперь будем окаймлять минор М1, т.е. будем строить всевозможные миноры 2-ого порядка, ктр. содержат в себе i-тую строку и j-тый столбец, до тех пор, пока не найдем ненулевой минор 2-ого порядка.

М2 (i, i1, j.j1)

Дальше аналогично строим миноры 3-го порядка, окаймляющие М2 (минор), до тех пор, пока не получим минор, отличный от нуля.

Процесс будет продолжаться до одного из событий:
1. размер минора достигнет числа к.

3. на каком-то этапе все окаймленные миноры окажутся = 0.

В обоих случаях величина ранга-матрицы будет равна порядку большего отличного от нуля минора.

Метод элементарных преобразований:
как известно, понятие треугольной матрицы определяется только для квадратных матриц. Для прямоугольных матриц аналогом является понятие трапецивидной матрицы.

Определение вектора

Вектор АВ^-> – направленный отрезок прямой (АВ) с нач.в т.А и концом в т.В. При умнож.вектора на число «У» получается коллинеарный в-р.

Длина в-ров |АВ|= кв.корень х²+у²

В-ры,лежащие на одной прямой наз-ся коллинеарными. В-ры,лежащие в одной плоскости или ||-ных плоскостях наз-ся компланарными. Если нач.и конец вектора совп.,то в-р наз-ют нулевым. Длина нул.вект.=0.

Вектором,противоп-м в-ру а^->,наз-ся произвед.в-ра а^->на ч-ло (-1),т.е. - а^->=(-1)а^->.

Координатами в-ра а^-> наз-ся корд-ты его конечной точки. На плоскости Oxy два ч-ла - (х;у), в пространстве Oxyz три ч-ла - (х;у;z).

В-р а^-> = (x;y;z) мож.б.записан в виде а^-> = хi^-> +yj^->+zk^->. i^->,j^->,k^-> – единичные в-ры(орты),совпадающие с направл.соотв.осей Ох,Оу,Оz. хi^->,уj^->,zk^-> - компоненты в-ра.

Операции над в-ми:

1) Суммой двух в-ров а^-> и b^-> наз-ся в-р с^->=а^->+ b^->,нач.кот.совп-т с нач.в-ра а^->, а конец – с концом в-ра b^->при усл.,что нач.в-ра b^-> совп.с концом в-ра а^->.

Правило треугольника. Для слож.2-х в-ров а^->и b^-> по правилу треуг-ка оба эти в-ра переносятся ||-но самим себе так,чтобы нач.одного из них совп.с концом другого. Тогда в-р суммы задаётся 3-ей стороной образовавшегося треуг-ка, причём его нач.совп.с нач.первого в-ра.

2)умнож.в-ра на ч-ло:при умнож.в-ра на ч-ло Y пол-ся коллинеарный в-р. (Произвед.в-ра а^-> на ч-ло У наз-ся в-р b^->=Уа^->,имеющий длину |b^->|=|У||а^->|,направление кот.совп.с направл.в-ра а^->, если У<0.) Если b^->= а^->Y,то а^->|| b^->. И наоб.,если а^->|| b^->( а^->не=0),то b^->= а^->Y.

3) Разностью 2-х в-ров а^->и b^-> наз-ся сумма в-ра а^-> и в-ра -b^->,противоположного b^->.

||Скалярным произведением 2-х в-ров наз-ся ч-ло,равное произведению длин этих в-ров на косинус угла между ними: а^-> * b^-> *cosф, где ф-угол между в-рами а^-> и b^->. В-ры явл-ся ||-ми тогда и только тогда, когда их скал.произвед.=0.

||n-мерным в-ром наз-ся упорядоченная совокуп.n действительных чисел,записываемых в виде х=(х₁,х₂,..,х_n),где числа х₁,х₂,х₃,..х_n компоненты в-ра.

Равенство в-ров.Векторы х и y равны тогда и только тогда, когда равны их соотв.компоненты,т.е. х=у,если х_i=у_j, i=1,2,…,n.

Суммой 2-х в-ров одинак.размерности n наз-ся в-р z=x+y,компоненты кот.равны сумме соотв.компонент слагаемых в-ров,т.е.z_i=x_i+y_i,i=1,2,...,n.

Произв-м в-ра на действит.ч-ло Y наз-ся в-р u=Yx,комп-ты кот.равны произв-ю Y на соотв.комп-ты в-ра х,т.е. u_i = Yx_i, i=1,2,...,n.

Линейные оп-ции над люб.в-рами удовлет.след.св-вам: 1)х+у=у+х – коммутативное, 2)(х+у)+z=х+(у+z) – ассоциативное(сочетательное), 3)альфа(бета*х)=(альфа*бета)х, 4)альфа(х+у)=альфа*х+альфа*у, 5)(альфа*бета)х=альфа*х+бета*х, 6)сущ-т нул.в-р 0=(0,0,…,0)такой,что х+0=х для люб.в-ра х., 7)для люб.в-ра сущ-т противоп.в-р (-х) такой,что х+(-х)=0., 8)1*х=х для люб.в-ра х.

Базис

Базис — это линейно независимая совокупность векторов, которая порождает всё пространство. В конечномерном пространстве существует конечный базис, и тогда любой вектор пространства может быть единственным образом представлен в виде разложения вида

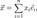где — это базис, а — координаты вектора в заданном базисе.

Прямая линия на плоскости.

Напомним сведения об уравнении прямой на плоскости. Любое уравнение первой степени относительно неизвестных х и у является уравнением прямой на плоскости: АX + ВY + С = 0

Оно может быть записано в некоторых специальных видах:

а) уравнение с угловым коэффициентом у= kx+b , где k - угловой коэффициент, численно равный тангенсу угла наклона прямой к положительному направлению оси Ох , а свободный член b - ордината точки пересечения графика и Оу.

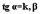-отрезок, отсекаемый графиком на оси оу

б) уравнение пучка прямых, проходящих через точку (х0 ,у0) у-у0 = k(х-х0 )

в) уравнение прямой, проходящей через две заданные точки (х1у1) и (х2у2)

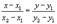
Плоскость в пространстве.

Простейшей поверхностью является плоскость. Плоскость в пространстве можно задавать различными способами. Каждому из них соответствует определенный вид ее уравнения.

Общее уравнение плоскости.

В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение

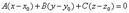
определяет плоскость, проходящую через точку 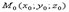и имеющей нормальный вектор .

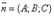Раскрывая в уравнении (1) скобки и обозначая число 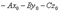буквой D, представим его в виде

.

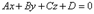Это уравнение называется общим уравнением плоскости.

Угол между двумя плоскостями:

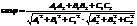
Условие параллельности прямых заключается в равенстве их угловых коэффициентов.

tgφ1=tgφ2 или k1=k2

Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1

k1*k2=-1

Расстояние от точки до плоскости:

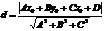
Матрицы и действия над матрицами.

Матрица- прямоуг таблица чисел, содерж m-строк и n-столбцов.

1.Матрицы равны между собой, если равны соответств элементы этих матриц.

2.Матрица, в которой m=n наз квадратной или n-ого порядка.

3.Квадратная матрица, у которой все элементы, кроме элементов гл диагонали, равны 0 называется диагональной.

4.Диаг матрица, у которой каждый элемент главной диаг =1 наз единичной.

5.Квадратная матрица наз. треугольной, если все элементы, расположенные по одну сторону её гл диаг =0.

6.Матрица, у которой все числа, стоящие на гл диаг не нулевые, а также некоторое кол ненулевых строк, наз трапециевидной.

7.Матрица, содерж один столбец или строку, наз вектором из Rⁿ пространства.

Действия:

Сложение – только для матриц одинакового размера.

Умножение на число. Множества матриц одинакового размера обознач M^m*n. Тогда введённое на этом мн-ве операции сложения и умнож на число превращ M^m*n в линейное пр-во, векторами которого явл матрицы m*n.

Умножение на вектор-столбец. Для умножения матрицы на вектор-столбец надо, чтобы число столбцов матрицы было равно числу координат вектора.

Две матрицы наз эквивалентными, если одна из них получена из другой с помощью элементарным преобраз. любую матрицу можно привести к канонической.

Определители второго и третьего порядка.
Определителем второго порядка, соответствующим таблице элементов

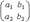
называется число a1 b2 - a2 b1. Определитель второго порядка обозначается так:

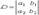
Определитель третьего порядка, соответствующий таблице элементов

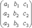
определяется равенством