Степень с рациональным показателем

Степень с рациональным показателем

Если:

• a > 0;

• n — натуральное число;

• m — целое число;

Тогда:

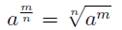
Пример 2.

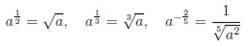
Свойства степеней

Произведение степеней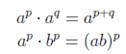
Деление степеней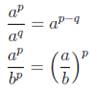
Возведение степени в степень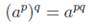

Пример 3.

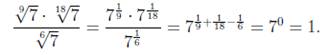
Корень

Арифметический квадратный корень

Уравнение 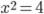имеет два решения: x=2 и x=-2. Это числа, квадрат которых равен 4.

Рассмотрим уравнение 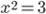. Нарисуем график функции 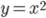и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.

Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень 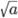— это неотрицательное число, квадрат которого равен 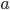, a ≥ 0. При a < 0 — выражение 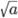не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу .

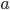Корень из квадрата

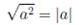
Например, 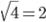. А решения уравнения 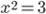соответственно 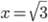и

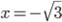
Кубический корень

Кубический корень из числа 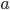— это число, куб которого равен 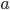. Кубический корень определен для всех 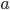. Его можно извлечь из любого числа: .

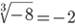Корень n-ой степени

Корень 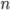-й степени из числа 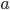— это число, 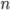-я степень которого равна .

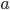Если 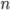— чётно.

• Тогда, если a < 0 корень n-ой степени из a не определен.

• Или если a ≥ 0, то неотрицательный корень уравнения 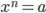называется арифметическим корнем n-ой степени из aи обозначается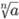

Если 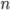— нечётно.

• Тогда уравнение 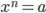имеет единственный корень при любом .

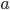Пример 4.

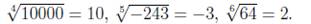
Понятие арксинуса и арккосинуса числа. Примеры. И 3 вопрос

Арксинус, арккосинус, арктангенс и арккотангенс – основные сведения.

Задача, обратная нахождению значений синуса, косинуса, тангенса и котангенса данного угла, подразумевает нахождение угла по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.

В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение обговорим некоторые тонкости, касающиеся этой темы, и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.

Навигация по странице.

• Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.

• Обозначения arcsin, arccos, arctg и arcctg.

• Примеры.

• Арксинус, арккосинус, арктангенс и арккотангенс числа или угла?

• Арксинус, арккосинус, арктангенс и арккотангенс на единичной окружности.

Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа

Дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.

Определение.

Арксинус числа a из интервала от −1 до 1 включительно – это такой угол, лежащий в пределах от −π/2 до π/2 (от −90 до 90 градусов) включительно, синус которого равен a.

Определение.

Арккосинусом числа a, −1≤a≤1, называется такой угол из отрезка [0, π] (от нуля до180 градусов включительно), косинус которого равен a.

Определение.

Арктангенсом числа a, a – любое действительное число, называется угол из интервала(−π/2, π/2) (от −90 до 90 градусов не включительно), тангенс которого равен a.

Определение.

Арккотангенс числа a, a – любое действительное число, - это такой угол из интервала(0, π) (от нуля до 90 градусов не включительно), котангенс которого равен a.

Из приведенных определений видно, что арксинус и арккосинус числа определены для чисел, лежащих в интервале [−1, 1], для остальных чисел арксинус и арккосинус не определяются. Например, не определены arcsin 2, арксинус пяти, арксинус минус корня из трех, арккосинус семи целых двух третьих и арккосинус минус пи, так как числа 2, 5, 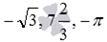не лежат в интервале от −1 до 1.

В свою очередь определения арктангенса и арккотангенса даются для любых действительных чисел a. То есть, имеют смысл и арктангенс нуля, и арктангенс −500,2, и арккотангенс миллиарда, и арккотангенс −π/3, как и арктангенс, и арккотангенс любого другого действительного числа.

Также стоит отметить, что при условиях, указанных для числа a в определениях, арксинус, арккосинус, арктангенс и арккотангенс существуют, причем они определены однозначно, то есть, для данного числа a имеют единственное значение.

К началу страницы

Примеры

Самое время привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.

Начнем с примеров арксинуса. Угол π/3 является арксинусом числа 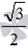, это действительно так, так как число 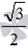принадлежит интервалу от −1 до 1, угол π/3 лежит в пределах от −π/2до π/2 и 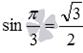. Приведем еще несколько примеров арксинуса числа: arcsin(−1)=−π/2,arcsin(0,5)=π/6, .

А вот π/10 не является арксинусом 1/2, так как sin(π/10)≠1/2. Еще пример: не смотря на то, что синус 270 градусов равен −1, угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.

Для полноты картины осталось привести примеры арккосинуса, арктангенса и арккотангенса числа. Например, угол 0 радиан является арккосинусом единицы (так как выполняются все условия из определения арккосинуса: число 1 лежит в отрезке от −1 до 1, угол нуль радиан лежит в пределах от нуля до пи включительно и cos0=1), угол π/2 есть арккосинус нуля. По определению арктангенса числа arctg(−1)=−π/4 и арктангенс корня из трех равен 60 градусам (π/3 рад). А из определения арккотангенса можно заключить, чтоarcctg0=π/2, так как π/2 лежит в открытом интервале от 0 до пи и ctg(π/2)=0.

К началу страницы

Логарифм и его свойства. Примеры

Логарифмом числа по основанию ( 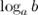) называется такое число , что 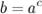, то есть запис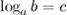и и 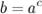равносильны. Логарифм имеет смысл, если .

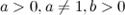Если немного перефразировать - Логарифм числа по основанию определяется как показатель степени, в которую надо возвести число , чтобы получить число (Логарифм существует только у положительных чисел).

Логарифм в переводе с греческого буквально означает "число, изменяющее отношение".

Специальные обозначения:

• Натуральный логарифм 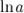- логарифм по основанию , где - число Эйлера.

• Десятичный логарифм 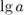- логарифм по основанию 10.

Свойства логарифмов:

1° 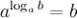- основное логарифмическое тождество.

2°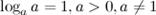

3°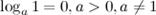

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4° 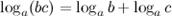- логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5° 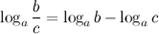- логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6° 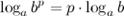- логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°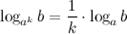

8°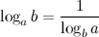

9° 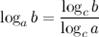- переход к новому основанию.

Вычислить 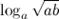, если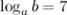

Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:

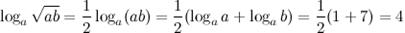
Ответ.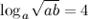

Степень с рациональным показателем

Если:

• a > 0;

• n — натуральное число;

• m — целое число;

Тогда:

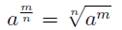
Пример 2.

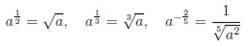
Свойства степеней

Произведение степеней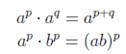
Деление степеней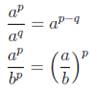
Возведение степени в степень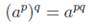

Пример 3.

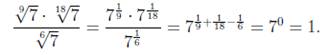
Корень