Построение эпюр в статически неопределимых системах. Метод перемещений

Сущность метода

Как уже говорилось выше, в статически неопределимых системах (в отличие от систем статически определимых) распределение внутренних сил зависит от упругих свойств элементов системы. Поэтому для определения всех усилий в конструкции одних только уравнений равновесия недостаточно, и в общем случае нужно дополнительно составлять физические и геометрические уравнения, описывающие условия деформации системы. При этом какие-то факторы выбирают в качестве основных неизвестных. Эти величины должны вполне определять напряженно-деформированное состояние системы, т.е. через них можно выразить все остальные неизвестные.

Если в методе сил в качестве таких основных неизвестных выбираются внутренние усилия в фиксированных сечениях конструкции, то в методеперемещений за основные неизвестные принимаются перемещения фиксированных сечений или узлов системы. Число неизвестных перемещений, принимаемых за основные, называется степенью кинематическойнеопределимости. Оно, вообще говоря, не связано со степенью статической неопределимости данной конструкции. Число и вид неизвестных перемещений назначают так, чтобы через них достаточно легко могли быть выражены все прочие факторы системы, в частности внутренние усилия в ее элементах.

Для иллюстрации сказанного рассмотрим абсолютно жесткий брус, поддерживаемый четырьмя одинаковыми стержнями с жесткостью на растяжение ЕА (рис.49,а). Такая система является трижды статически неопределимой. В то же время удлинения, а следовательно, и усилия всех стержней вполне определяются одним перемещением, например вертикальным перемещением точки В, которое обозначим через Z₁.

Рис. 49

Степень статической неопределимости зависит от числа вертикальных стержней, в то время как степень кинематической неопределимости такой системы остается равной единице при любом числе стержней.

Метод расчета таких систем, рассматриваемый в традиционном курсе сопротивления материалов, также предполагает использование картины деформаций системы, но не является методом перемещений. Здесь же мы рассмотрим решение в форме, характерной для метода перемещений.

Определим усилия в стержнях N₁, N₂, N₃, N₄, принимая в качестве неизвестного перемещение Z₁. Устраним перемещение Z₁, введя по его направлению дополнительную связь (рис.49,б). Сформированную таким образом систему назовем основной системой метода перемещений. Сообщим введенной связи принудительное смещение Z₁, которое определим из условия равенства нулю суммарной реакции R₁ в этой связи, так как в действительности сама связь отсутствует. Будем считать реакцию положительной, если ее направление совпадает с принятым направлением перемещения, и отрицательной – в противном случае.

В основной системе от нагрузки F реакция в связи (рис.49,б). От смещения Z₁ для линейно-упругой системы реакция в связи пропорциональна перемещению Z₁. Представим ее в виде: , где r₁₁ – реакция от единичного смещения (рис.49,в). Согласно принципу суперпозиции условие отсутствия полной реакции в присоединенной связи имеет вид:

(4.1)

или

(4.2)

Составляя сумму моментов относительно точки О (рис.49,в), находим:

Из уравнения (4.2) получим:

Усилия в стержнях, показанные на рис.49,в, найдены от единичного смещения умножая их на фактическое перемещение z₁, получим искомые значения сил:

Разрешающее уравнение (4.2) выражает в соответствующей форме условие равновесия системы, получившей под нагрузкой F перемещение z₁; иначе говоря, это уравнение равновесия системы, выраженное через перемещение z₁.

Аналогичные рассуждения можно провести и для рамных систем, где использование метода перемещений является особенно эффективным.

Рассмотрим плоскую раму (рис.50,а) в деформированном состоянии как совокупность отдельных стержневых элементов, объединенных в узлах. Деформированное состояние каждого элемента вполне определяется нагрузкой, непосредственно приложенной к этому элементу, и перемещениями его концевых сечений. Отдельные стержни, показанные на рис.50,а, деформированы так же как и в составе рамы, что достигается смещением концевых сечений стержней на величины, равные перемещениям узлов рамы.

Если пренебречь изменением длин стержней в процессе деформации, то в целом деформированное состояние рамы будет определено тремя перемещениями узлов: z₁ – горизонтальным линейным смещением ригеля; z₂ и z₃ – углами поворотов узлов, т.е. степень кинематической неопределимости рамы равна трем.

Основная система с присоединенными связями, устраняющими эти перемещения, показана на рис.50,б. Условные защемления, введенные в узлы и устраняющие их углы поворотов, называются плавающими заделками, так как считается, что устраняя поворот, они не препятствуют соответствующему линейному смещению узла. При устранении связи 1 рама деформируется без поворота узлов (рис.50,в).

Уравнения равновесия рамы, выраженные через перемещения z₁, z₂ и z₃ получим, приравнивая нулю суммарные реакции в присоединенных связях (сосредоточенная сила в линейной связи) и моменты в угловых связях:

(4.3)

Система уравнений (4.3) является разрешающей системой для рассматриваемой рамы по методу перемещений. Для того чтобы можно было развернуть каждое из равенств (4.3), нужно предварительно изучить работу отдельных стержней, составляющих основную систему, на воздействие

Рис. 50

различных видов нагрузки и смещений опорных закреплений. Если предварительно вычислить реакции по концам стержней от указанных воздействий, то, используя принцип суперпозиции, каждую из полных реакций (4.3) можно записать как сумму слагаемых, выражающих каждое воздействие отдельно.

4.2 Вспомогательная таблица метода перемещений

Как было показано в предыдущем параграфе, при расчете методом перемещений исходная система путем введения дополнительных связей расчленяется на ряд однопролетных статически неопределимых балок. Очевидно, что характер нагружения таких балок и способы закрепления их концов дают определенный, постоянный "набор" возможных вариантов, к определенной совокупности которых приводит расчетная схема любой заданной системы. Поэтому целесообразно заранее рассчитать однопролетные статически неопределимые балки при разных нагрузках и использовать эти результаты по мере необходимости. Обычно такой "набор" возможных вариантов представляется в табличной форме.

Рассмотрим несколько примеров, иллюстрирующих результаты, указанных в тех или иных строках приведенной таблицы.

1. Загружение сосредоточенной силой F однопролетной балки с жестким защемлением на одном конце и шарнирно подвижным опиранием на другом (строка 1 вспомогательной таблицы).

Для решения задачи используем метод сил. Эквивалентная система, единичная и грузовая эпюры для заданной схемы (рис.51,а) представлены на рис.51,б,в,г.

Рис. 51

Каноническое уравнение метода сил:

Коэффициенты канонических уравнений вычислим по способу Верещагина:

Вспомогательная таблица метода перемещений.

№	Схема балки и воздействия на нее	Эпюра моментов и реакции
		;
		; ;
		;
		;
	Неравномерный нагрев	h – высота сечения

№	Схема балки и воздействия на нее	Эпюра моментов и реакции
	Неравномерный нагрев	h – высота сечения

Отметим, что при указанных условиях закрепления концов балки коэффициент 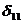не зависит от характера внешнего воздействия.

Так как и, следовательно, то

Подставляя 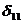и в каноническое уравнение, находим:

Тогда реакции левой опоры и опорный момент будут:

Окончательная эпюра моментов для заданной, теперь уже статически определимой, системы, загруженной силами F и X₁ (рис.51,д), показана на рис.51,е.

2. Загружение равномерно распределенной нагрузкой q (рис.52,а) однопролетной статически неопределимой балки (строка 2 вспомогательной таблицы).

Для решения вновь используем метод сил. Эпюра моментов от внешней нагрузки, приложенной к основной системе, показана на рис.52,б, а единичная эпюра моментов (и, соответственно, перемещение 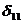) совпадает с построенной в предыдущем примере (рис.51,в).

Уравнение метода сил:

Рис. 52

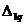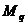Здесь при вычислении использованы эпюры (рис.51,в) и (рис.52,б).

Реакция лишней связи:

X₁

Реакция левой опоры:

Опорный момент в левой опоре получим, просуммировав момент в этом сечении от нагрузки q с моментом от X₁:

Направление опорных реакций и момента в заделке показаны на рис.52,в, а окончательная эпюра моментов – на рис.52,г.

3. Перемещение заделки на величину D по направлению перпендикулярному оси стержня (рис.53,а).

Эпюра изгибающих моментов в основной системе от смещения D будет нулевой, поэтому нулевым будет свободный член уравнения метода сил.

А перемещение по направлению Х₁ (рис.53,б) будет:

D_1D=D,

и уравнение метода сил принимает вид:

где то же, что и ранее.

Отсюда последовательно находим реакции и опорный момент :

Направление этих величин показаны на рис.53,в, а окончательная эпюра моментов на рис.53,г.

При единичном смещении D=1 все вычисленные величины принимают значения, указанные в строке 4 вспомогательной таблицы метода перемещений.

Аналогичным образом можно рассчитать однопролетную балку на другие виды воздействий. Предоставив читателю возможность самостоятельно проделать соответствующие расчеты, отметим только, что при рассмотрении балки с двумя защемленными концами (строки 6 – 10 вспомогательной таблицы метода перемещений) целесообразно выбирать основную систему, разрезая балку посредине пролета. Такой разрез, как известно, приводит к появлению трех лишних неизвестных в методе сил – продольной и поперечной сил, а также изгибающего момента. Однако при всех рассматриваемых видах воздействий (вертикальные нагрузки, линейные смещения заделок по нормали к оси балки, поворот заделок) продольная сила будет равна нулю, поэтому решение всех задач приводит к системе двух канонических уравнений метода сил.

Рис. 53