Понятие о классификации линий второго порядка.
Линии второго порядка
Лекция 14
Эллипс. Гипербола. Парабола
Эллипс
Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых до данных точек 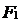 и
и 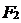 равна длине данного отрезка
равна длине данного отрезка 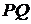 , где
, где 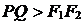 .
.
Коротко можно записать определение эллипса 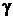 так:
так:
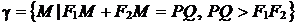 . (37)
. (37)
Точки 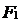 и
и 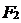 называются фокусами эллипса, а расстояние между ними - фокальным расстоянием.
называются фокусами эллипса, а расстояние между ними - фокальным расстоянием.
Если  - точка данного эллипса, то отрезки
- точка данного эллипса, то отрезки 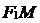 и
и 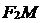 (а также их длины) называются фокальными радиусами точки
(а также их длины) называются фокальными радиусами точки  .
.
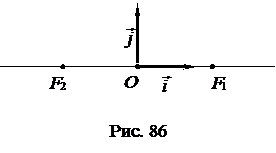 Пусть на плоскости даны две различные точки
Пусть на плоскости даны две различные точки 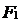 и
и 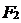 . Обозначим через
. Обозначим через 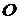 середину отрезка
середину отрезка 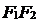 . Рассмотрим прямоугольную декартову систему координат
. Рассмотрим прямоугольную декартову систему координат 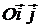 , где
, где 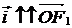 (рис. 86).
(рис. 86).
Выведем уравнение эллипса 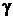 с фокусами
с фокусами 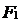 и
и 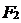 в системе координат
в системе координат 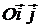 .
.
Пусть 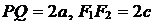 .
.
Замечание. Так как 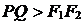 , то для эллипса всегда
, то для эллипса всегда 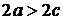 , т.е.
, т.е.
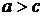 .
.
Пусть 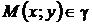 . Так как
. Так как 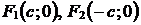 в
в 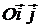 , то
, то
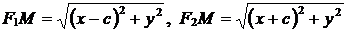 .
.
По определению эллипса 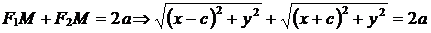 . Преобразуем это уравнение:
. Преобразуем это уравнение:
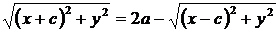 ;
;
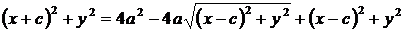 ;
;
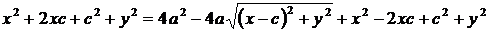 ;
;
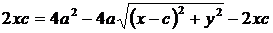 ;
;
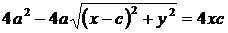 ;
;
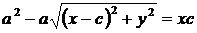 ;
;
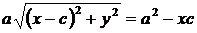 .
.
Возведем обе части последнего уравнения в квадрат:
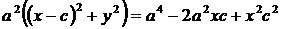 ;
;
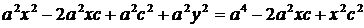 ;
;
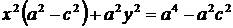 .
.
Разделим обе части этого уравнения на 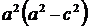 :
:
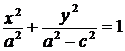 .
.
Так как для эллипса 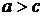 , то
, то 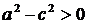 . Положим
. Положим 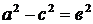 . Тогда
. Тогда
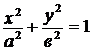 , где
, где 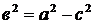 . (38)
. (38)
Итак, доказано, что если 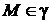 , то координаты точки
, то координаты точки  удовлетворяют уравнению (38).
удовлетворяют уравнению (38).
Докажем, что если координаты точки  удовлетворяют уравнению (38), то она принадлежит эллипсу
удовлетворяют уравнению (38), то она принадлежит эллипсу 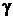 .
.
Пусть 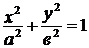 , где
, где 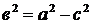 ,
, 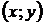 - координаты точки
- координаты точки  .
.
Найдем 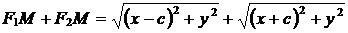 . Выразим
. Выразим 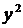 из уравнения
из уравнения 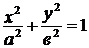 :
:
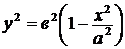 .
.
Тогда, учитывая, что 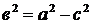 , получим:
, получим:
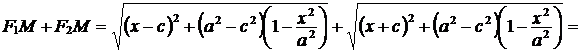
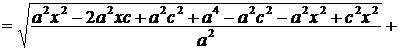
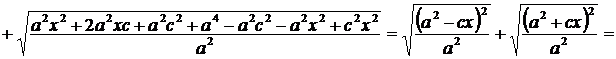
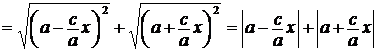 .
.
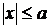 и
и 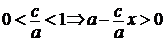 и
и 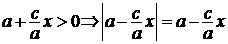 и
и 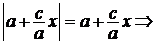
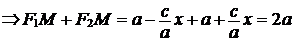 . Из условия (37) следует, что
. Из условия (37) следует, что 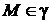 .
.
Итак, уравнение (38) есть уравнение эллипса. Оно называется каноническим уравнением эллипса.
Если 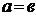 , то
, то 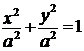 , т.е.
, т.е. 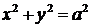 - уравнение окружности радиуса
- уравнение окружности радиуса 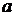 .
.
Пользуясь каноническим уравнением эллипса, докажем геометрические свойства эллипса, которые понадобятся для построения изображения эллипса.
Свойства эллипса
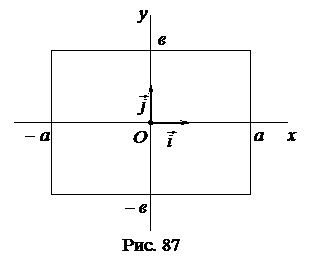 1°. Из уравнения (38) следует, что
1°. Из уравнения (38) следует, что 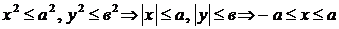 ,
, 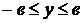 . Следовательно, все точки эллипса принадлежат прямоугольнику, центр которого находится в точке
. Следовательно, все точки эллипса принадлежат прямоугольнику, центр которого находится в точке 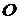 , стороны параллельны осям
, стороны параллельны осям 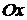 и
и 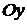 и равны соответственно
и равны соответственно 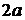 и
и 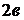 (рис. 87).
(рис. 87).
2°. Симметрия относительно начала координат и осей координат.
Пусть 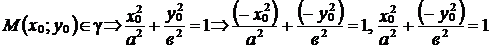 и
и 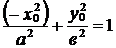 . Из первого тождества следует, что
. Из первого тождества следует, что 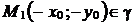 , из второго – что
, из второго – что 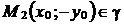 , из третьего – что
, из третьего – что 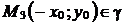 , а это означает, что эллипс
, а это означает, что эллипс 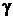 симметричен относительно начала координат, оси
симметричен относительно начала координат, оси 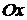 и оси
и оси 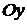 соответственно. Таким образом, точка
соответственно. Таким образом, точка 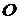 является центром симметрии, оси
является центром симметрии, оси 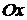 и
и 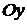 - осями симметрии эллипса
- осями симметрии эллипса 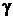 .
.
Прямая, проходящая через фокусы, называется первой (фокальной) осью симметрии, а перпендикулярная к ней ось – второй осью симметрии эллипса.
3°. Точки пересечения эллипса с осями симметрии.
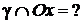
Чтобы найти точки пересечения эллипса 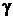 с осью
с осью 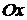 , надо решить систему их уравнений:
, надо решить систему их уравнений:

Решая систему, получаем: 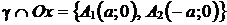 .
.
Аналогично находим, что 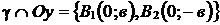 .
.
Точки пересечения эллипса со своими осями симметрии называются вершинами эллипса. Таким образом, эллипс имеет четыре вершины.
Отрезки 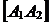 и
и 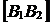 называются соответственно большой и малой «осями» эллипса, а положительные числа
называются соответственно большой и малой «осями» эллипса, а положительные числа 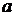 и
и 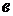 - большой и малой «полуосями» эллипса.
- большой и малой «полуосями» эллипса.
4°. Выясним, как выглядит часть эллипса, расположенная в первой координатной четверти.
Возьмем в первой координатной четверти произвольную точку 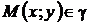 , тогда
, тогда 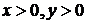 . Следовательно, функция
. Следовательно, функция 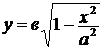 монотонно убывает от
монотонно убывает от 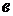 до 0, если
до 0, если 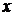 возрастает от 0 до
возрастает от 0 до 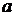 .
.
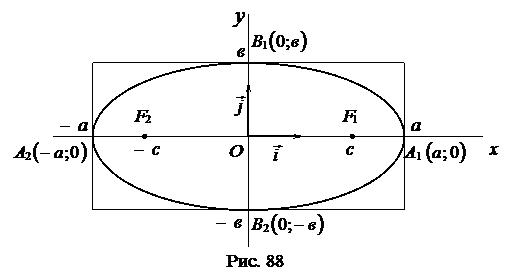
Учитывая свойства 1°- 4°, построим изображение эллипса (рис. 88):
 |
Число 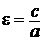 называется эксцентриситетом эллипса. Так как для эллипса
называется эксцентриситетом эллипса. Так как для эллипса 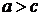 , то
, то 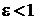 . У окружности
. У окружности 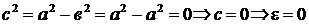 . При
. При 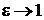 уменьшается «высота» эллипса.
уменьшается «высота» эллипса.
Директрисами эллипса называются две прямые, параллельные второй оси и отстоящие от нее на расстоянии 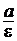 .
.
Уравнения директрис:
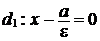 или
или 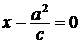 ;
;
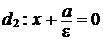 или
или 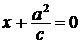 (рис. 89).
(рис. 89).
У окружности 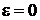 , следовательно, она не имеет директрис.
, следовательно, она не имеет директрис.
Эллипс обладает следующим директориальным свойством: для любой точки  , принадлежащей эллипсу, отношение расстояния от
, принадлежащей эллипсу, отношение расстояния от  до фокуса к расстоянию от
до фокуса к расстоянию от  до соответствующей директрисы равно эксцентриситету, т.е.
до соответствующей директрисы равно эксцентриситету, т.е.
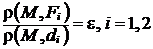 (рис. 89).
(рис. 89).
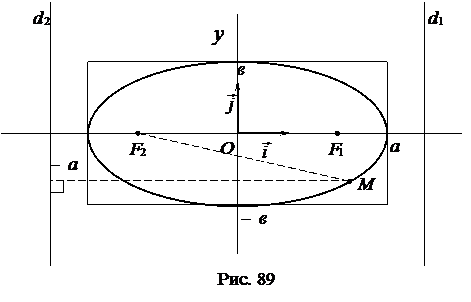 |
| |
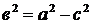 , то
, то 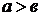 . В случае, когда
. В случае, когда 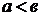 , фокусы эллипса будут лежать на оси
, фокусы эллипса будут лежать на оси 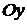 , а директрисы будут параллельны оси
, а директрисы будут параллельны оси 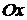 .
. Замечание 2. Директрисы эллипса не имеют общих точек с эллипсом.
Задания для самостоятельной работы
1. Приведите уравнение эллипса к каноническому виду:
а) 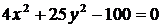 ; ; | в) 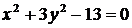 ; ; |
б) 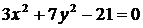 ; ; | г) 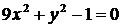 . . |
2. Дано каноническое уравнение эллипса. Найдите большую и малую «полуоси», координаты вершин, координаты фокусов, фокальное расстояние, фокальные радиусы точки  , эксцентриситет, уравнения директрис:
, эксцентриситет, уравнения директрис:
а) 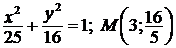 ; ; |
б) 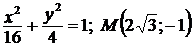 . . |
3. Постройте изображение эллипса, его фокусов и директрис:
а) 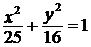 ; ; | б) 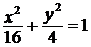 . . |
Гипербола
Гиперболой называется множество всех точек плоскости, абсолютное значение разности расстояний каждой из которых до данных точек 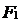 и
и 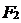 равно длине данного отрезка
равно длине данного отрезка 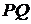 , где
, где 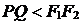 .
.
Коротко можно записать определение гиперболы 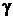 так:
так:
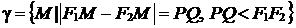 . (39)
. (39)
Точки 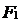 и
и 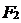 называются фокусами гиперболы, а расстояние между ними - фокальным расстоянием.
называются фокусами гиперболы, а расстояние между ними - фокальным расстоянием.
Если  - точка данной гиперболы, то отрезки
- точка данной гиперболы, то отрезки 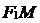 и
и 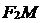 (а также их длины) называются фокальными радиусами точки
(а также их длины) называются фокальными радиусами точки  .
.
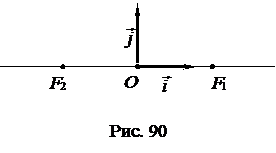 Пусть на плоскости даны две различные точки
Пусть на плоскости даны две различные точки 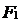 и
и 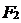 . Обозначим через
. Обозначим через 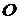 середину отрезка
середину отрезка 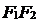 . Рассмотрим прямоугольную декартову систему координат
. Рассмотрим прямоугольную декартову систему координат 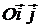 , где
, где 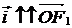 (рис. 90).
(рис. 90).
Выведем уравнение гиперболы 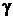 с фокусами
с фокусами 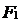 и
и 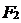 в системе координат
в системе координат 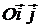 .
.
Пусть 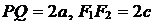 .
.
Замечание. Так как 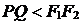 , то для гиперболы всегда
, то для гиперболы всегда 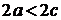 , т.е.
, т.е.
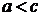 .
.
Пусть 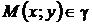 . Так как
. Так как 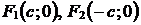 в
в 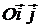 , то
, то
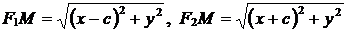 .
.
По определению гиперболы 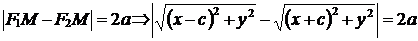 . Преобразуем это уравнение:
. Преобразуем это уравнение:
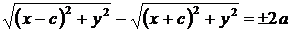 ;
;
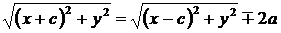 ;
;
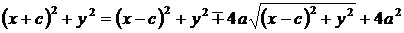 ;
;
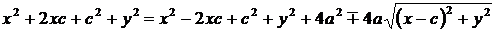 ;
;
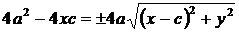 ;
;
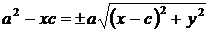 .
.
Возведем обе части последнего уравнения в квадрат:
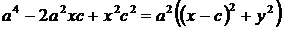 ;
;
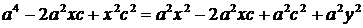 ;
;
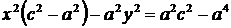 .
.
Разделим обе части этого уравнения на 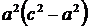 :
:
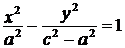 .
.
Так как для гиперболы 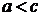 , то
, то 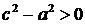 . Положим
. Положим 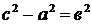 . Тогда
. Тогда
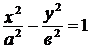 , где
, где 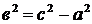 . (40)
. (40)
Итак, доказано, что если 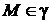 , то координаты точки
, то координаты точки  удовлетворяют уравнению (40).
удовлетворяют уравнению (40).
Докажем, что если координаты точки  удовлетворяют уравнению (40), то она принадлежит гиперболе
удовлетворяют уравнению (40), то она принадлежит гиперболе 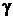 .
.
Пусть 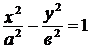 , где
, где 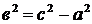 ,
, 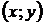 - координаты точки
- координаты точки  .
.
Найдем 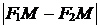 . Выразим
. Выразим 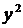 из уравнения
из уравнения 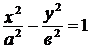 :
:
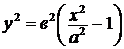 .
.
Найдем 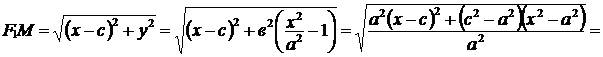
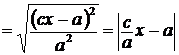 .
.
Аналогично 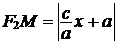 .
.
|
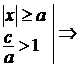
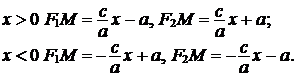
Тогда 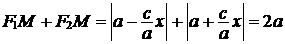 .
.
Из условия (39) следует, что 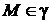 .
.
Итак, уравнение (40) есть уравнение гиперболы. Оно называется каноническим уравнением гиперболы.
Пользуясь каноническим уравнением гиперболы, докажем геометрические свойства гиперболы, которые понадобятся для построения изображения гиперболы.
Свойства гиперболы
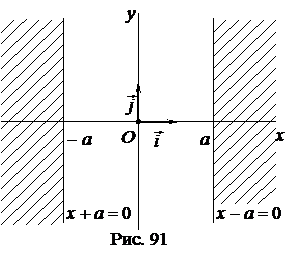 |
1°. Из уравнения (40) следует, что 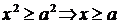 или
или 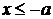 . Следовательно, все точки гиперболы лежат вне полосы, ограниченной прямыми
. Следовательно, все точки гиперболы лежат вне полосы, ограниченной прямыми 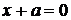 и
и 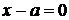 (рис. 91).
(рис. 91).
2°. Симметрия относительно начала координат и осей координат.
Пусть 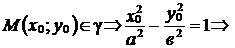
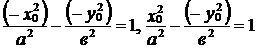 и
и 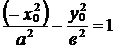 . Из первого тождества следует, что
. Из первого тождества следует, что 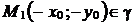 , из второго – что
, из второго – что 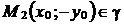 , из третьего – что
, из третьего – что 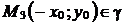 , а это означает, что гипербола
, а это означает, что гипербола 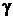 симметрична относительно начала координат, оси
симметрична относительно начала координат, оси 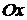 и оси
и оси 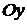 соответственно. Таким образом, точка
соответственно. Таким образом, точка 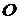 является центром симметрии, оси
является центром симметрии, оси 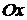 и
и 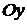 - осями симметрии гиперболы
- осями симметрии гиперболы 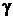 .
.
Прямая, проходящая через фокусы, называется действительной осью симметрии, а перпендикулярная к ней ось – мнимой осью симметрии гиперболы.
3°. Точки пересечения гиперболы с осями симметрии.
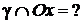
Чтобы найти точки пересечения гиперболы 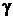 с осью
с осью 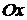 , надо решить систему их уравнений:
, надо решить систему их уравнений: 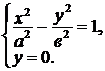
Решая систему, получаем: 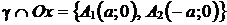 .
.
Аналогично находим, что 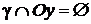 .
.
Точки пересечения гиперболы со своими осями симметрии называются вершинами гиперболы. Таким образом, гипербола имеет две вершины.
Отрезки 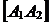 и
и 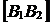 называются соответственно действительной и мнимой «осями» гиперболы, а положительные числа
называются соответственно действительной и мнимой «осями» гиперболы, а положительные числа 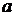 и
и 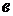 - действительной и мнимой «полуосями» гиперболы.
- действительной и мнимой «полуосями» гиперболы.
4°. Найдем точки пересечения гиперболы с прямой 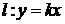 .
.
Для этого решим систему 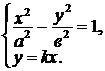
Получаем уравнение 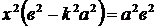 . Корни
. Корни 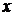 - это абсциссы точки пересечения прямой
- это абсциссы точки пересечения прямой 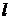 с
с 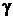 . Рассмотрим три случая:
. Рассмотрим три случая:
1) Если 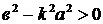 , т.е.
, т.е. 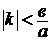 , то
, то 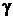 и
и 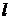 имеют две общие точки;
имеют две общие точки;
2) Если 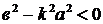 , т.е.
, т.е. 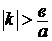 , то
, то 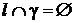 ;
;
3) 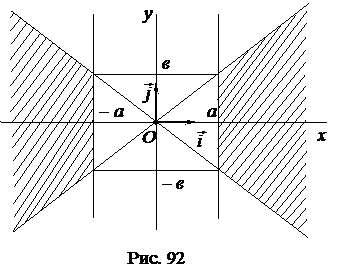 Если
Если 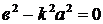 , т.е.
, т.е. 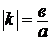 , то
, то 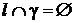 .
.
Следовательно, все точки гиперболы расположены в заштрихованных областях (рис. 92). Гипербола имеет две ветви.
Случаю 3) соответствуют две прямые 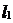 и
и 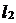 с угловыми коэффи-
с угловыми коэффи-
циентами 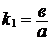 и
и 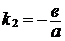 . Эти прямые (
. Эти прямые ( 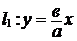 и
и 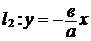 ) называются асимптотами гиперболы.
) называются асимптотами гиперболы.
При неограниченном возрастании абсолютной величины абсциссы точки  гиперболы точка
гиперболы точка  неограниченно приближается к асимптоте.
неограниченно приближается к асимптоте.
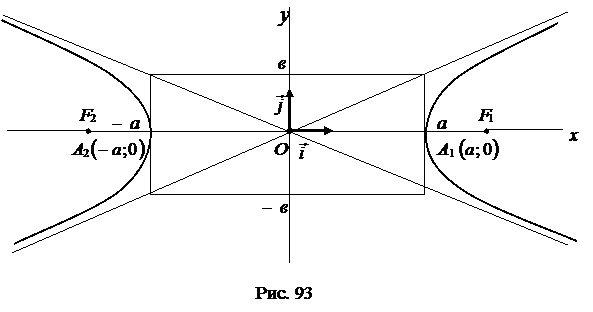 Учитывая свойства 1°- 4°, построим изображение гиперболы (рис. 93):
Учитывая свойства 1°- 4°, построим изображение гиперболы (рис. 93):
Число 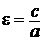 называется эксцентриситетом гиперболы. Так как для гиперболы
называется эксцентриситетом гиперболы. Так как для гиперболы 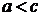 , то
, то 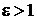 . Чем больше
. Чем больше 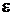 , тем больше гипербола «вытянута» вдоль мнимой оси.
, тем больше гипербола «вытянута» вдоль мнимой оси.
Гипербола, у которой 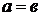 , называется равносторонней. Ее каноническое уравнение
, называется равносторонней. Ее каноническое уравнение 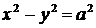 . Уравнения ее асимптот
. Уравнения ее асимптот 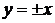 .
.
Директрисами эллипса называются две прямые, параллельные мнимой оси и отстоящие от нее на расстоянии 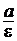 .
.
Уравнения директрис:
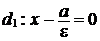 или
или 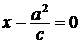 ;
;
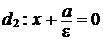 или
или 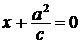 (рис. 94).
(рис. 94).
Гипербола обладает следующим директориальным свойством: для любой точки  , принадлежащей гиперболе, отношение расстояния от
, принадлежащей гиперболе, отношение расстояния от  до фокуса к расстоянию от
до фокуса к расстоянию от  до соответствующей директрисы равно эксцентриситету, т.е.
до соответствующей директрисы равно эксцентриситету, т.е.
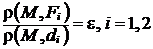 (рис. 94).
(рис. 94).
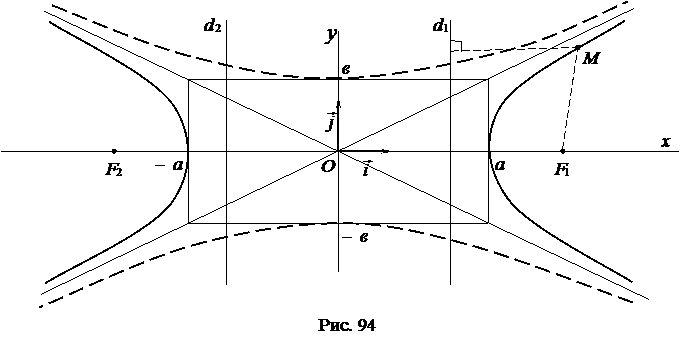
Замечание 1. Директрисы гиперболы не имеют общих точек с гиперболой.
Гипербола 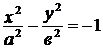 называется сопряженной к гиперболе
называется сопряженной к гиперболе 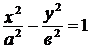 . Ее мнимой осью является ось
. Ее мнимой осью является ось 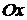 (на рис. 94 она изображена пунктиром).
(на рис. 94 она изображена пунктиром).
Задания для самостоятельной работы
1. Приведите уравнение гиперболы к каноническому виду:
а) 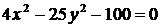 ; ; | в) 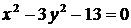 ; ; |
б) 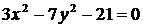 ; ; | г) 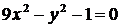 . . |
2. Дано каноническое уравнение гиперболы. Найдите действительную и мнимую «полуоси», координаты вершин, координаты фокусов, фокальное расстояние, фокальные радиусы точки  , эксцентриситет, уравнения директрис:
, эксцентриситет, уравнения директрис:
а) 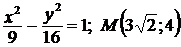 ; ; |
б) 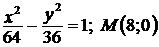 . . |
3. Постройте изображение гиперболы, ее фокусов и директрис:
а) 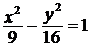 ; ; | б) 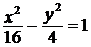 . . |
4. Докажите, что эксцентриситет равносторонней гиперболы равен 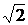 .
.
Парабола
Параболой называется множество всех точек плоскости, расстояние каждой из которых до данной точки 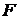 равно расстоянию до данной прямой
равно расстоянию до данной прямой 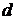 , не содержащей точку
, не содержащей точку 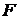 .
.
Точка 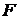 называется фокусом параболы, а прямая
называется фокусом параболы, а прямая 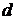 - директрисой.
- директрисой.
Расстояние 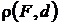 от фокуса до директрисы называется фокальным параметром параболы и обозначается через
от фокуса до директрисы называется фокальным параметром параболы и обозначается через 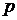 :
:
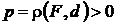 .
.
Коротко определение параболы 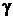 можно записать так:
можно записать так:
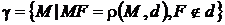 .
.
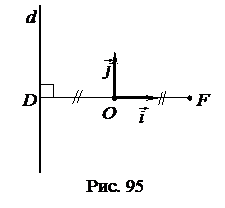 Пусть на плоскости дана прямая
Пусть на плоскости дана прямая 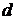 и точка
и точка 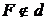 . Проведем из точки
. Проведем из точки 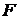 перпендикуляр
перпендикуляр 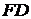 к прямой
к прямой 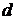 . Выберем прямоугольную декартову систему координат
. Выберем прямоугольную декартову систему координат 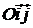 так, чтобы точка
так, чтобы точка 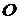 была серединой отрезка
была серединой отрезка 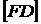 , а
, а 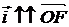 (рис. 95).
(рис. 95).
Выведем уравнение параболы 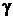 с фокусом
с фокусом 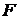 и директрисой
и директрисой 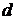 в системе координат
в системе координат 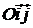 .
.
Найдем координаты точки 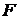 и прямой
и прямой 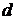 в системе
в системе 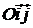 :
: 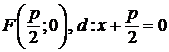 .
.
Пусть 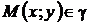 . Тогда по определению параболы
. Тогда по определению параболы 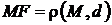 . Учитывая, что
. Учитывая, что 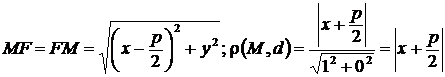 , получим:
, получим:
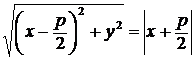 .
.
Преобразуем это уравнение:
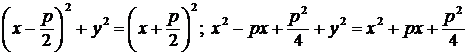 ;
;
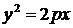 . (42)
. (42)
Итак, если точка  принадлежит параболе
принадлежит параболе 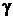 , то ее координаты удовлетворяют уравнению (42).
, то ее координаты удовлетворяют уравнению (42).
Пусть, обратно, координаты точки 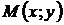 удовлетворяют уравнению (42), т.е.
удовлетворяют уравнению (42), т.е.
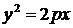 .
.
Тогда 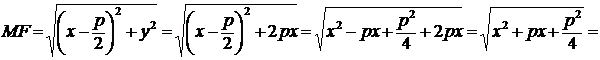
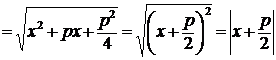 ; а
; а 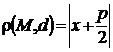 . Следовательно,
. Следовательно, 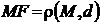 , т.е.
, т.е. 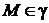 (по определению параболы).
(по определению параболы).
Таким образом, доказано, что уравнение (42) есть уравнение параболы 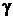 с фокусом
с фокусом 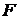 и директрисой
и директрисой 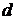 . Уравнение (42) называется каноническим уравнением параболы.
. Уравнение (42) называется каноническим уравнением параболы.
Чтобы изобразить параболу по ее каноническому уравнению, исследуем геометрические свойства параболы.
Свойства параболы
1°. Так как 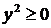 и
и 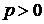 , то из уравнения (42) следует, что
, то из уравнения (42) следует, что 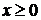 , т.е. все точки параболы принадлежат полуплоскости
, т.е. все точки параболы принадлежат полуплоскости 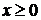 .
.
2°. Выясним, симметрична ли парабола 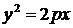 относительно начала координат и осей координат.
относительно начала координат и осей координат.
Пусть 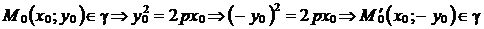 , т.е. парабола симметрична относительно оси
, т.е. парабола симметрична относительно оси 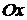 . Ось симметрии параболы называется осью параболы.
. Ось симметрии параболы называется осью параболы.
Заметим, что 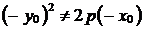 и
и 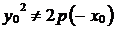 , следовательно,
, следовательно, 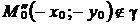 и
и 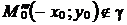 , т.е. парабола не симметрична относительно начала координат и оси
, т.е. парабола не симметрична относительно начала координат и оси 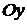 .
.
3°. Найдем точки пересечения параболы с осями координат.
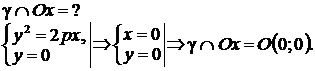
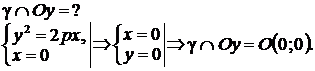
Таким образом, парабола имеет одну вершину.
4°. Зависимость формы параболы от ее фокального параметра.
Чем больше фокальный параметр 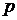 , тем сильнее парабола вытягивается вдоль оси
, тем сильнее парабола вытягивается вдоль оси 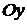 .
.
5°. Чтобы изобразить параболу, найдем координаты четырех вспомогательных точек, принадлежащих параболе.
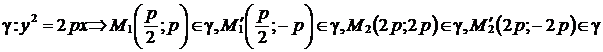 .
.
Построение изображения параболы по ее каноническому уравнению выполняется в следующей последовательности: выбираем на плоскости прямоугольную декартову систему координат 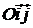 ; строим точки
; строим точки 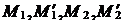 ; проводим через точки
; проводим через точки 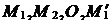 и
и 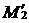 параболу; строим фокус
параболу; строим фокус 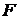 и директрису
и директрису 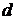 (рис. 96).
(рис. 96).
 |
Эксцентриситетом параболы называется число единица.
Из определения параболы 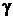 следует, что
следует, что 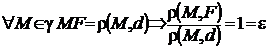 , т.е. для параболы также имеет место директориальное свойство.
, т.е. для параболы также имеет место директориальное свойство.
Директриса параболы также никогда не пересекает параболу.
Если построить параболы 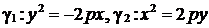 и
и 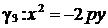 в той же канонической системе координат
в той же канонической системе координат 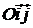 , то они будут расположены так (рис. 97):
, то они будут расположены так (рис. 97):

Заметим, что на ось параболы в ее каноническом уравнении указывает та переменная, которая стоит в первой степени.
Задания для самостоятельной работы
1. Приведите к каноническому виду уравнение параболы:
а) 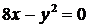 ; ; | г) 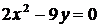 ; ; |
б) 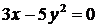 ; ; | д) 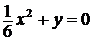 ; ; |
в) 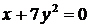 ; ; | е) 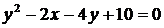 . . |
2. Дано каноническое уравнение параболы. Найдите фокальный параметр параболы, координаты фокуса и уравнение директрисы:
а) 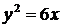 ; ; | в) 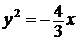 ; ; |
б) 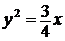 ; ; | г) 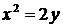 . . |
3. Изобразите параболу, ее фокус и директрису:
а) 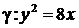 ; ; | в) 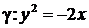 ; ; |
б) 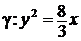 ; ; | г) 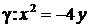 . . |
Лекция 15
К каноническому виду
По виду общего уравнения трудно определить тип линии второго порядка. Для этого общее уравнение линии второго порядка надо привести к каноническому виду. Это делают с помощью преобразования прямоугольной декартовой системы координат 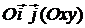 , в которой дано общее уравнение (43) линии. С помощью поворота координатных векторов и переноса начала получают каноническую систему координат
, в которой дано общее уравнение (43) линии. С помощью поворота координатных векторов и переноса начала получают каноническую систему координат 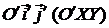 , в которой уравнение данной линии второго порядка имеет канонический вид.
, в которой уравнение данной линии второго порядка имеет канонический вид.
Итак, пусть линия второго порядка 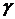 задана в системе
задана в системе 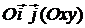 общим уравнением
общим уравнением 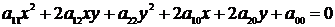 .
.
Если 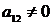 , то приведение общего уравнения линии
, то приведение общего уравнения линии 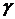 к каноническому виду происходит в два этапа:
к каноническому виду происходит в два этапа:
I этап. С помощью поворота координатных векторов освобождаются от члена, содержащего произведение 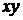 . Угол поворота
. Угол поворота 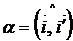 находят следующим образом:
находят следующим образом:
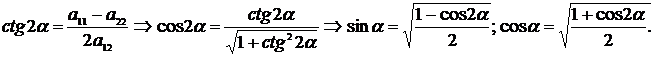
Тогда координаты координатных векторов 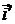 и
и 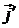 в системе
в системе 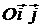 будут находиться так:
будут находиться так:
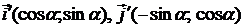 . (44)
. (44)
Записываем формулы поворота координатных векторов на угол 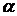 :
:
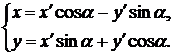 (45)
(45)
Подставляем 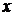 и
и 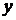 из формул (45) в общее уравнение линии
из формул (45) в общее уравнение линии 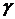 . После преобразований исчезает член
. После преобразований исчезает член 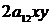 . Получаем уравнение линии
. Получаем уравнение линии 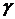 в промежуточной системе координат
в промежуточной системе координат 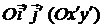 .
.
II этап. Выделяем полные квадраты при 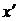 и
и 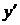 и совершаем перенос начала
и совершаем перенос начала 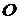 в точку
в точку 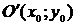 по формулам
по формулам
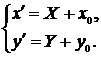 (46)
(46)
Координаты 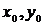 точки
точки 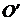 вычислены в системе
вычислены в системе 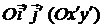 .
.
Подставляем 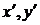 из формул (46) в уравнение линии
из формул (46) в уравнение линии 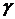 в системе
в системе 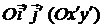 . После преобразований получаем каноническое уравнение линии
. После преобразований получаем каноническое уравнение линии 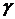 в новой системе
в новой системе 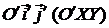 и определяем ее вид.
и определяем ее вид.
Строим старую систему координат 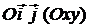 , промежуточную
, промежуточную 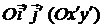 , новую
, новую 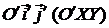 и линию
и линию 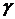 по ее каноническому уравнению в системе
по ее каноническому уравнению в системе 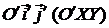 .
.
Замечание 1. При переходе ко II этапу возможны следующие случаи:
1.Уравнение содержит переменные 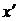 и
и 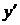 во второй степени. Тогда выделяются полные квадраты при
во второй степени. Тогда выделяются полные квадраты при 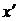 и
и 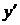 . В результате может получиться каноническое уравнение эллипса, гиперболы, мнимого эллипса, пары пересекающих
. В результате может получиться каноническое уравнение эллипса, гиперболы, мнимого эллипса, пары пересекающих
