Методы интегрирования определенного интеграла
12.4. Геометрическое приложение определенного интеграла
Несобственный интеграл
Определенный интеграл с переменным верхним пределом интегрирования и его свойства.
Если функция 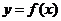 интегрируема на
интегрируема на 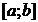 , то она интегрируема на любом
, то она интегрируема на любом
Если функция 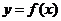 интегрируема на
интегрируема на 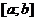 , то она интегрируема на любом меньшем отрезке и следовательно для любого
, то она интегрируема на любом меньшем отрезке и следовательно для любого 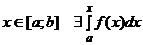 . Чтобы не смешивать обозначения верхнего предела и переменной интегрирования, будем записывать его в виде
. Чтобы не смешивать обозначения верхнего предела и переменной интегрирования, будем записывать его в виде 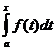 .
.
Определение. Для функции 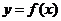 , интегрируемой на
, интегрируемой на 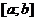 , интеграл вида
, интеграл вида
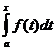 , где
, где 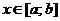 , называется интегралом с переменным верхним пределом
, называется интегралом с переменным верхним пределом
интегрирования.
Рассмотрим функцию 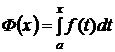 .
.
Теорема 1. Если  интегрируема на
интегрируема на 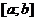 , то
, то 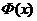 непрерывна на
непрерывна на 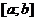 .
.
Теорема 2. Если  непрерывна на
непрерывна на 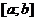 , то
, то 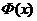 дифференцируема на
дифференцируема на 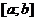 и ее производная
и ее производная 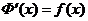 (иначе говоря: производная интеграла с переменным верхним пределом равна значению подынтегральной функции на верхнем пределе интегрирования).
(иначе говоря: производная интеграла с переменным верхним пределом равна значению подынтегральной функции на верхнем пределе интегрирования).
Доказательство. 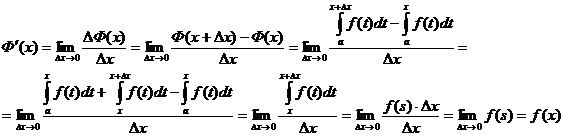 так как при
так как при 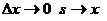 вследствие непрерывности функции
вследствие непрерывности функции  на
на 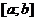 по условию.
по условию.
Следствие. Определенный интеграл с переменным верхним пределом функции  является первообразной для функции
является первообразной для функции  .
.
Формула Ньютона-Лейбница - основная формула интегрального исчисления.
Теорема. Пусть  непрерывна на
непрерывна на 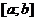 и
и 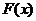 какая-либо первообразная
какая-либо первообразная
для  , тогда
, тогда 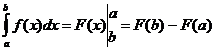 .
.
Доказательство. Так как 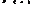 - первообразная
- первообразная  на
на 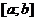 по условию и
по условию и 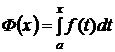 первообразная для
первообразная для  на
на 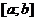 по теореме 1, то
по теореме 1, то 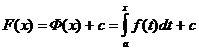 . Будем поочередно считать
. Будем поочередно считать 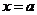 и
и 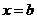 , тогда
, тогда 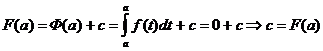
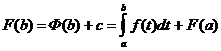 , т.е.
, т.е. 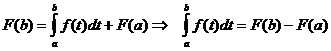 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница.
Отметим еще два варианта формулы:
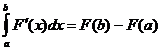 ,
, 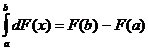 .
.
Пример. 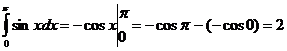 .
.
Методы интегрирования определенного интеграла.
а) Метод непосредственного интегрирования определенного интеграла основан на применении таблицы интегралов, свойств интеграла, формулы Ньютона-Лейбница и элементарных преобразований подынтегральной функции.
Пример. 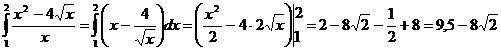
б) Метод интегрирования по частям.
Теорема. Пусть 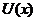 и
и 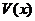 имеют непрерывные производные на
имеют непрерывные производные на 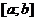 , тогда
, тогда 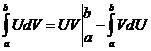
в) Метод подстановки (замена переменной)
Теорема. Пусть 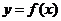 непрерывна на
непрерывна на 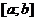 , а функция
, а функция 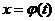 имеет
имеет
непрерывную производную на 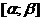 и при
и при 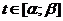 значения
значения 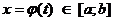 , причем
, причем 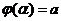 ,
, 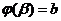 , тогда
, тогда 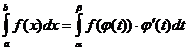 .
.
Пример. 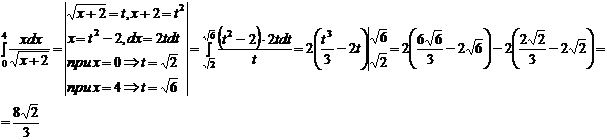
Геометрические приложения определенного интеграла.
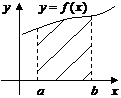 1) Вычисление площадей плоских фигур.
1) Вычисление площадей плоских фигур.
Если 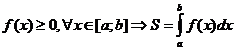 .
.
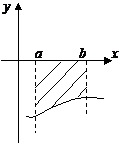 |
Если 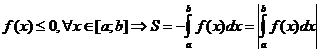 .
.
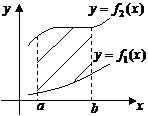 |
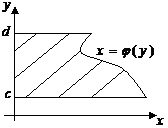 Если
Если 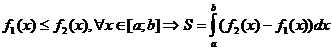 .
.
Если 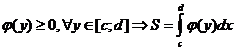 .
.
Если фигура ограничена кривой, заданной параметрически, то есть
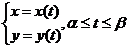 , тогда
, тогда 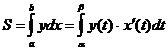 .
.
2) Вычисление длин друг кривых.
Пусть кривая L задана явно, то есть 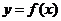 ,
, 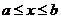 , тогда длина
, тогда длина 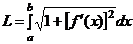 .
.
Если L задана параметрически 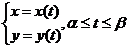 , то
, то 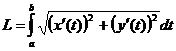 .
.
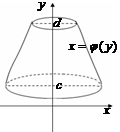
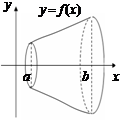 3) Вычисление объемов тел вращения.
3) Вычисление объемов тел вращения.
Пусть 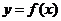 ,
, 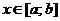 . Будем вращать кривую
. Будем вращать кривую 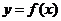 вокруг оси 0X, тогда объем тела, полученного при вращении кривой, вычисляют по формуле
вокруг оси 0X, тогда объем тела, полученного при вращении кривой, вычисляют по формуле
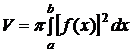 .
.
Если же кривую 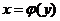 ,
, 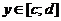 вращать вокруг оси 0Y, то
вращать вокруг оси 0Y, то
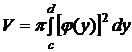 .
.
Несобственные интегралы.
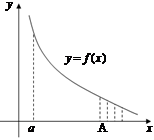 Рассмотрим
Рассмотрим 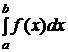 . Функция
. Функция  определена на конечном промежутке
определена на конечном промежутке 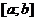 и ограничена на нем. Если нарушается хотя бы одно из двух требований, то мы имеем дело с несобственным интегралом.
и ограничена на нем. Если нарушается хотя бы одно из двух требований, то мы имеем дело с несобственным интегралом.
1. Пусть нарушается требование конечности чисел a и (или) b. При этом возможны случаи:
1) пусть  определена на
определена на 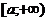 и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке 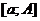 , где
, где 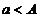 .
.
Несобственным интегралом первого рода называется 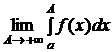 и обозначается
и обозначается 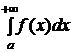 , то есть
, то есть 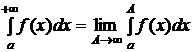 (1).
(1).
Если предел в правой части равенства (1) существует и конечен, то несобственный интеграл называется сходящимся и его значение равно пределу правой части. В противном случае несобственный интеграл называется расходящимся.
 2) пусть
2) пусть  определена на
определена на  и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке  ,
, 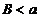
Несобственный интеграл первого рода в этом случае определяется по формуле 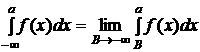 (2).
(2).
3) пусть  определена на
определена на 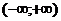 и интегрируема на каждом конечном отрезке этого интервала, тогда
и интегрируема на каждом конечном отрезке этого интервала, тогда 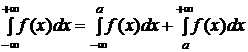 (3), причем несобственный интеграл в левой части называется сходящимся, если сходятся оба интеграла в правой части равенства (3). Если хотя бы один из них расходится, то расходится интеграл в левой части.
(3), причем несобственный интеграл в левой части называется сходящимся, если сходятся оба интеграла в правой части равенства (3). Если хотя бы один из них расходится, то расходится интеграл в левой части.
Замечание. Если 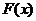 первообразная функции
первообразная функции  на
на 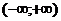 , тогда справедлива обобщенная формула Ньютона-Лейбница
, тогда справедлива обобщенная формула Ньютона-Лейбница 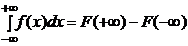 , где
, где 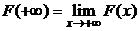 ,
, 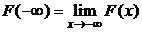 .
.
Пример. 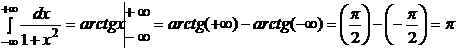
2. Пусть нарушается требование ограниченности функции  .
.
1) Пусть функция 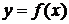 непрерывна на
непрерывна на 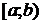 и
и 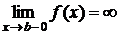 , тогда
, тогда 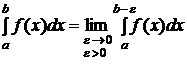 (4).
(4).
2) Если 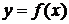 непрерывна на
непрерывна на 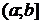 и
и 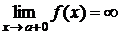 , тогда
, тогда 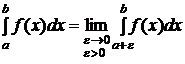 (5).
(5).
Интегралы в левой части равенств (4) и (5) называются сходящимися, если в правой части этих равенств предел существует и конечен и значение несобственного интеграла равно пределу правой части. Если в правой части равенств (4) и (5) пределы не существуют или бесконечны, то несобственные интегралы в левой части этих формул называются расходящимися.
 3) Если
3) Если 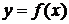 непрерывна на
непрерывна на 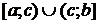 и
и 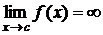 , тогда
, тогда 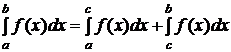 (6).
(6).
Интеграл в левой части равенства (6) называется сходящимся, если сходятся оба интеграла в правой части этой формулы; и расходящимся, если расходится хотя бы один из интегралов в правой части этой формулы.
Пример. Установить сходимость интеграла 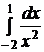 .
.
Так как 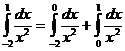 и
и 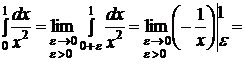
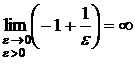 , то есть
, то есть 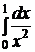 расходится, и потому данный интеграл
расходится, и потому данный интеграл 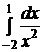 расходится.
расходится.
