Определение неопределенного интеграла и его основные свойства.
Если 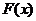 – первообразная функции
– первообразная функции 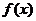 на
на 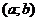 , то для функции
, то для функции 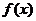
первообразными будет множество функций вида 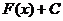 .
.
Определение. Совокупность всех первообразных функции 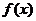 на интервале
на интервале 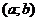 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 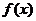 на
на 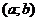 и обозначается
и обозначается 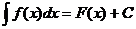 .
.
Нахождение функции по ее производной называется интегрированием функции. Для проверки правильности интегрирования надо взять производную от полученного результата, при этом должна быть получена подынтегральная функция. Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование. Рассмотрим основные линейные и нелинейные свойства неопределенного интеграла:
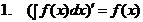
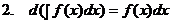
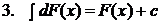
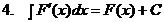
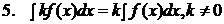
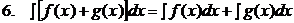
Доказательство 2.
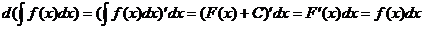 .
.
Таблица неопределенных интегралов.
1. 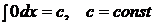 ,
, 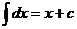 ,
,
2. 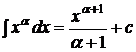 ,
, 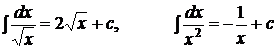 ,
,
3. 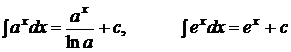 ,
,
4. 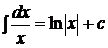 ,
,
5. 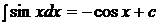 ,
, 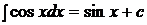 ,
,
6. 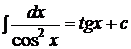 ,
, 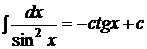 ,
,
7. 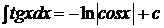 ,
, 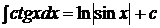 ,
,
8. 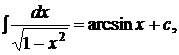
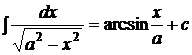 ,
,
9. 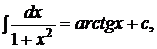
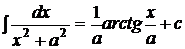 ,
,
10. 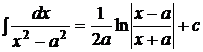 ,
, 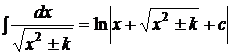 .
.
Основные методы интегрирования функций.
а) Метод непосредственного интегрирования основан на свойствах неопределенного интеграла, применении таблицы интегралов и элементарных преобразований функций.
Пример 1. 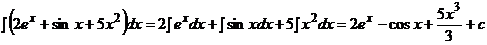 .
.
Пример 2. 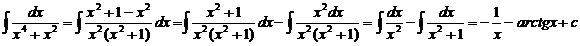 . Пример 3.
. Пример 3. 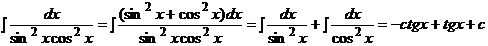 .
.
б) Интегрирование по частям.
Теорема. Пусть 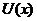 и
и 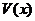 – две дифференцируемые функции на
– две дифференцируемые функции на 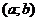 , тогда выполняется равенство
, тогда выполняется равенство 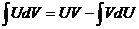 .
.
Доказательство. Рассмотрим формулу 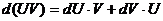 . Интегрируя обе части равенства, получим
. Интегрируя обе части равенства, получим 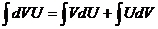 или
или 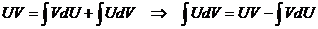 (*)
(*)
Эта формула позволяет свести нахождение 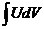 к нахождению интеграла
к нахождению интеграла 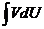 , который может оказаться более простым.
, который может оказаться более простым.
Замечания:
Формула (*) применима, если под интегралом одна из функций является алгебраической, другая – трансцендентной, причем если производная трансцендентной функции является также трансцендентной функцией, то за U принимают алгебраическую функцию, если же производная трансцендентной функции – алгебраическая функция, то за U принимают трансцендентную функцию.
За U обычно принимают функцию, которую трудно интегрировать.
Типы интегралов, берущихся по частям.
1) 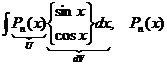 – многочлен, 2)
– многочлен, 2) 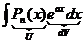 , 3)
, 3) 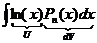 ,
,
4) 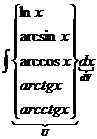 , 5)
, 5) 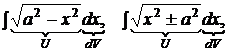 , 6)
, 6) 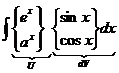 .
.
Интегралы 5 и 6 берутся применением формулы (*) дважды. В результате получается уравнение относительно исходного интеграла. Если в формуле 6 за U взята функция  , то при повторном интегрировании за U вновь принимаем
, то при повторном интегрировании за U вновь принимаем  .
.
Пример. 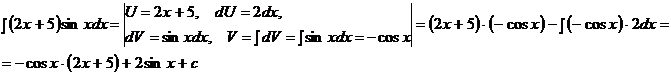 в) Интегрирование методом замены переменной.
в) Интегрирование методом замены переменной.
Теорема 1. Пусть функция 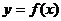 непрерывна на
непрерывна на  , а функция
, а функция 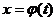 имеет непрерывную производную
имеет непрерывную производную 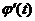 на
на 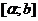 , причем при
, причем при 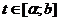 значение
значение 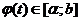 и существует обратная функция
и существует обратная функция 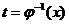 , тогда справедлива формула
, тогда справедлива формула 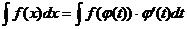 (1).
(1).
Пример. 
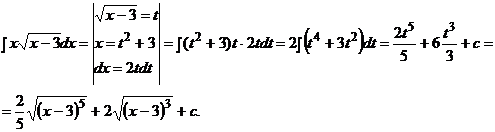
Частным случаем теоремы 1 является
Теорема 2. Если 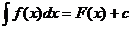 , то
, то 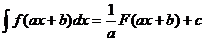 .
.
Формулой (1) пользуются и справа налево, тогда этот метод называется методом «подведения функции под знак дифференциала».
Пример.
1. 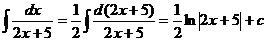 ,
,
2. 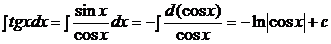 .
.
Лекция 10. Интегрирование некоторых классов функций.
Интегрирование простейших рациональных дробей.
Интегрирование рациональных дробей методом разложения на простейшие дроби.
Интегрирование некоторых тригонометрических функций.
Интегрирование некоторых иррациональных выражений. Некоторые тригонометрические подстановки.
