Кратные интегралы: определение, условия существования, основные свойства. Сведение к повторному интегралу
Кратные интегралы: определение, условия существования, основные свойства. Сведение к повторному интегралу
Пусть z=f(x,y) – непрерывно дифференцируемая и положительная функция двух переменных, определенная на ограниченном подмножестве (S) плоскости  . Если существует предел
. Если существует предел  независимо от выбора точек и независимо от разбиения множества (S) на элементарные части, то он называется двойным интегралом функции и обозначается
независимо от выбора точек и независимо от разбиения множества (S) на элементарные части, то он называется двойным интегралом функции и обозначается  .
.
Пусть дано некоторое тело (V) в трехмерном пространстве 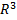 . Предположим, что известна плотность
. Предположим, что известна плотность  (x,y,z) распределения массы в каждой точке M(x,y,z) тела (V). Требуется определить всю массу тела. Если существует предел
(x,y,z) распределения массы в каждой точке M(x,y,z) тела (V). Требуется определить всю массу тела. Если существует предел  независимо от выбора точек (
независимо от выбора точек (  и независимо от разбиения множества (V) на элементарные части, то он называется тройным интегралом функции f(x,y,z) по множеству (V).
и независимо от разбиения множества (V) на элементарные части, то он называется тройным интегралом функции f(x,y,z) по множеству (V).
Свойства
Теорема 1: справедливо равенство 
Теорема 2: пусть функции f(x,y) и ϕ(x,y) определены на одном и том же множестве (S) плоскости  и на этом множестве не имеют двойные интегралы. Тогда справедлива формула
и на этом множестве не имеют двойные интегралы. Тогда справедлива формула
 , где А и В постоянные числа.
, где А и В постоянные числа.
Теорема 3: пусть функция f(x,y) определена на квадратируемом подмножестве (S) плоскости  . Предположим, что множество (S) некоторой кусочно-гладкой кривой разложено на два квадрируемые подмножества (S’) и (S’’). Тогда из существования двойного интеграла функции f(x,y) по области (S) следует существования двойных интегралов этой функции в обоих областях (S’) и (S’’), и обратно. При этом имеет место разложение
. Предположим, что множество (S) некоторой кусочно-гладкой кривой разложено на два квадрируемые подмножества (S’) и (S’’). Тогда из существования двойного интеграла функции f(x,y) по области (S) следует существования двойных интегралов этой функции в обоих областях (S’) и (S’’), и обратно. При этом имеет место разложение

Теорема 4: пусть f(x,y)  для всех (x,y)
для всех (x,y)  и существуют двойные интегралы функции f(x,y) и
и существуют двойные интегралы функции f(x,y) и  . Тогда справедливо равенство
. Тогда справедливо равенство 
Теорема 5: справедлива формула 
Теорема 6: (теорема о среднем) пусть функция двух переменных z=f(x,y) определена и интегрируема на замкнутом множетсве (S)с  . Тогда существует такая точка (ξ,η)
. Тогда существует такая точка (ξ,η)  (S), что
(S), что

Теорема 7: всякая непрерывная в области (S) функция z=f(x,y) интегрируема.
Теорема 8: если функция z=f(x,y) ограничена и имеет разрывы только лишь на конечном числе гладких кривых области (S), то она интегрируема.
Приведение двойного интеграла к повторному
Пусть функция двух переменных z=f(x,y) определена на прямоугольнике  , т.е. на множестве точек (x,y)
, т.е. на множестве точек (x,y)  , которые удовлетворяют условию
, которые удовлетворяют условию  где a<b, c<d
где a<b, c<d
Теорема: пусть для функции существует двойной интеграл  и также при каждом фиксированном x
и также при каждом фиксированном x  существует обычный интеграл I=
существует обычный интеграл I=  . Тогда существует повторный интеграл
. Тогда существует повторный интеграл

Работа плоского поля: формула Грина как частный случай теоремы Остроградского-Гаусса.
Пусть P(x,y) и Q(x,y) гладкие в области D, а Г – контур в области D, ограниченный под областью D. Тогда:

Формула Грина является частным случаем теоремы Остроградского-Гаусса, когда поверхность является плоской.
Кратные интегралы: определение, условия существования, основные свойства. Сведение к повторному интегралу
Пусть z=f(x,y) – непрерывно дифференцируемая и положительная функция двух переменных, определенная на ограниченном подмножестве (S) плоскости  . Если существует предел
. Если существует предел  независимо от выбора точек и независимо от разбиения множества (S) на элементарные части, то он называется двойным интегралом функции и обозначается
независимо от выбора точек и независимо от разбиения множества (S) на элементарные части, то он называется двойным интегралом функции и обозначается  .
.
Пусть дано некоторое тело (V) в трехмерном пространстве 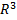 . Предположим, что известна плотность
. Предположим, что известна плотность  (x,y,z) распределения массы в каждой точке M(x,y,z) тела (V). Требуется определить всю массу тела. Если существует предел
(x,y,z) распределения массы в каждой точке M(x,y,z) тела (V). Требуется определить всю массу тела. Если существует предел  независимо от выбора точек (
независимо от выбора точек (  и независимо от разбиения множества (V) на элементарные части, то он называется тройным интегралом функции f(x,y,z) по множеству (V).
и независимо от разбиения множества (V) на элементарные части, то он называется тройным интегралом функции f(x,y,z) по множеству (V).
Свойства
Теорема 1: справедливо равенство 
Теорема 2: пусть функции f(x,y) и ϕ(x,y) определены на одном и том же множестве (S) плоскости  и на этом множестве не имеют двойные интегралы. Тогда справедлива формула
и на этом множестве не имеют двойные интегралы. Тогда справедлива формула
 , где А и В постоянные числа.
, где А и В постоянные числа.
Теорема 3: пусть функция f(x,y) определена на квадратируемом подмножестве (S) плоскости  . Предположим, что множество (S) некоторой кусочно-гладкой кривой разложено на два квадрируемые подмножества (S’) и (S’’). Тогда из существования двойного интеграла функции f(x,y) по области (S) следует существования двойных интегралов этой функции в обоих областях (S’) и (S’’), и обратно. При этом имеет место разложение
. Предположим, что множество (S) некоторой кусочно-гладкой кривой разложено на два квадрируемые подмножества (S’) и (S’’). Тогда из существования двойного интеграла функции f(x,y) по области (S) следует существования двойных интегралов этой функции в обоих областях (S’) и (S’’), и обратно. При этом имеет место разложение

Теорема 4: пусть f(x,y)  для всех (x,y)
для всех (x,y)  и существуют двойные интегралы функции f(x,y) и
и существуют двойные интегралы функции f(x,y) и  . Тогда справедливо равенство
. Тогда справедливо равенство 
Теорема 5: справедлива формула 
Теорема 6: (теорема о среднем) пусть функция двух переменных z=f(x,y) определена и интегрируема на замкнутом множетсве (S)с  . Тогда существует такая точка (ξ,η)
. Тогда существует такая точка (ξ,η)  (S), что
(S), что

Теорема 7: всякая непрерывная в области (S) функция z=f(x,y) интегрируема.
Теорема 8: если функция z=f(x,y) ограничена и имеет разрывы только лишь на конечном числе гладких кривых области (S), то она интегрируема.
Приведение двойного интеграла к повторному
Пусть функция двух переменных z=f(x,y) определена на прямоугольнике  , т.е. на множестве точек (x,y)
, т.е. на множестве точек (x,y)  , которые удовлетворяют условию
, которые удовлетворяют условию  где a<b, c<d
где a<b, c<d
Теорема: пусть для функции существует двойной интеграл  и также при каждом фиксированном x
и также при каждом фиксированном x  существует обычный интеграл I=
существует обычный интеграл I=  . Тогда существует повторный интеграл
. Тогда существует повторный интеграл

