Задачи на случайные величины

2.1. Из ящика с семью деталями, среди которых имеется 5 стандартных, наудачу взяты четыре детали. Составить закон распределения дискретной случайной величины Х числа стан­дартных деталей среди отобранных.

2.2. Тираж календаря 50 тыс. экземпляров. Вероятность брака в одном календаре равна 0,0003. Найти вероятность содержа­ния в тираже ровно 10 бракованных календарей.

2.3. Случайная составляющая дохода равна 2,5Х, а случайная составляющая затрат равна 40Y. Найти дисперсию прибыли при следующих условиях: случайная величина Х распределе­на по биномиальному закону с параметрами п = 100, р = 0,6; случайная величина Y распределена по закону Пуассона с па­раметром λ = 3; случайные величины Х и Y являются незави­симыми.

2.4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной законом распределения:

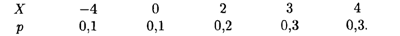
2.5. Найти дисперсию дискретной случайной величины Х — числа отказов реле в 10 независимых опытах, если вероятность отказа реле в каждом опыте равна 0,1.

2.6. Дискретная случайная величина Х задана законом рас­пределения:

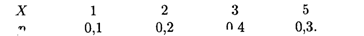
Найти центральные моменты первого, второго, третьего и чет­вертого порядков.

2.7. Найти ковариацию и коэффициент корреляции Х и Y для двумерной случайной величины, распределение которой следу­ющее:

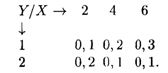
2.8. Непрерывная случайная величина Х задана на всей оси Ох функцией распределения F(x) = (arcctg x)/π. Найти веро­ятность того, что величина Х примет значение, заключенное в интервале (-1, 1).

2.9. Непрерывная случайная величина Х задана функцией распределения

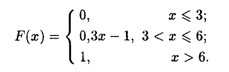
Найти вероятность того, что Х примет значение:а) менее 1; б) менее четырех;в) не менее четырех; г) не менее семи.

2.10. Дискретная случайная величина дана законом рапределения:

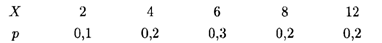
Найти функцию распределения и построить ее график.

2.11. Дана плотность распределения непрерывной случайной величины X:

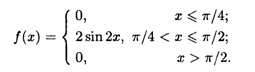
Найти функцию распределения F(x).

2.12. Случайная величина Х задана на положительной полу­оси Ох функцией распределения F(x) = 1 - е^-3x. Найти мате­матическое ожидание величины X.

2.13. Случайная величина Х задана на интервале (0, 2) плот­ностью распределения f(x) = x/8; вне этого интервала f(x) = 0. Найти функцию распределения и дисперсию величины X.

2.14. Случайная величина Х задана плотностью распределе­ния f(x) = 2e^-2x на интервале (0, ). Найти функцию распре­деления, математическое ожидание и дисперсию.

2.15. Случайная величина задана функцией распределения

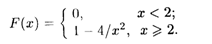
Найти плотность распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение.

2.16. Найти дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интер­вале (5, 10).

2.17. Сторона квадрата измерена приближенно в интервале (а, b). Найти математическое ожидание и дисперсию площа­ди квадрата, если его сторону рассматривать как случайную величину с равномерным распределением на этом интервале.

2.18. Размер женской обуви является случайной величиной с нормальным законом распределения, математическим ожида­нием 37 и дисперсией 4. Какой процент от общего объема за­купок следует предусмотреть магазину для обуви 38 размера, если этот размер находится в интервале (37,5, 38,5)?

2.19. Найти формулу плотности вероятности нормально рас­пределенной случайной величины X, если математическое ожидание равно 5, а дисперсия равна 36.

2.20. Случайная величина Х распределена нормально с мате­матическим ожиданием а = 10. Вероятность попадания Х в интервал (5, 10) равна 0,2. Найти дисперсию.

П6. Задания по теме "Линейное программирование"

6.1. Найти область решений и область допустимых решений системы неравенств

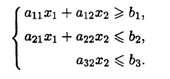
Значения коэффициентов системы ограничений системы неравенств

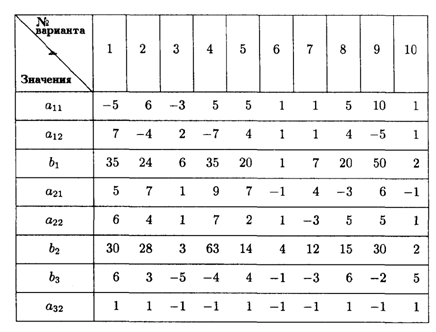
6.2. Найти область решений и область допустимых решений и определить координаты угловых точек области допустимых решений системы неравенств

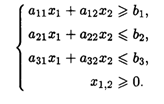
Значения коэффициентов системы ограничений системы неравенств

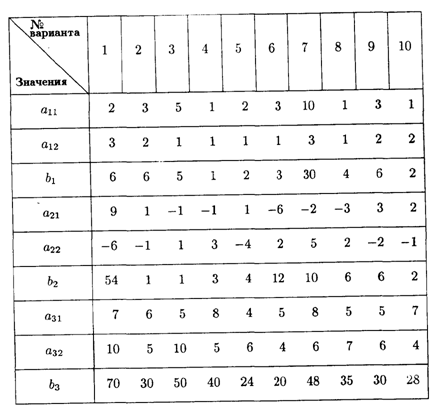
6.3. Дана задача линейного программирования

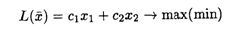
при ограничениях:

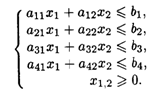
Графическим методом найти оптимальные решения при стремлении целевой функции к максимальному и минималь­ному значениям.

Значения коэффициентов целевой функции и системы ограничений

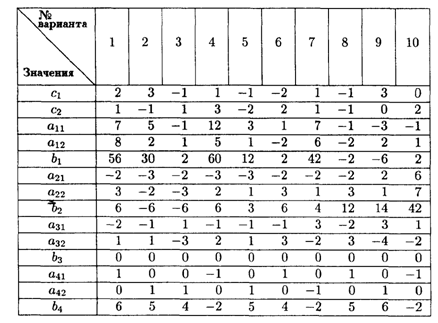
Составить математическую модель и провести экономичес­кий анализ задачи с использованием графического метода.

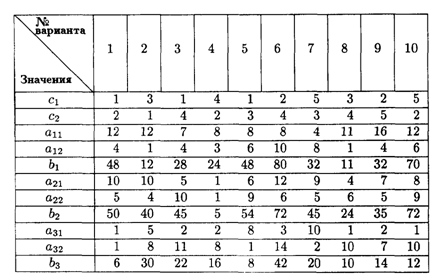
6.4. Фирма изготовляет два вида красок для внутренних (В) и наружных (Н) работ. Для их производства используют исход­ные продукты: пигмент и олифу. Расходы исходных продуктов и максимальные суточные запасы указаны в таблице.

Расход и суточные запасы исходных продуктов

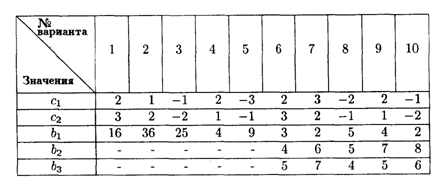
Изучение рынка сбыта показало, что суточный спрос на краску для наружных (внутренних) работ никогда не превы­шает b₃ т в сутки. Цена продажи 1 т краски для наружных работ — c₁ ден. ед., для внутренних работ — c₂ ден. ед.

Какое количество краски каждого вида должна произво­дить фирма, чтобы доход от реализации продукции был мак­симальным?

Значения коэффициентов условий задачи

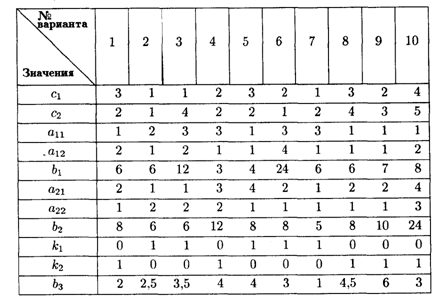
Примечание. Если по условию задания спрос на краску для наружных (внутренних) работ не превышает b₃ т в сутки, то в математической модели задачи следует принять, что коэффициент системы ограничений при неизвестном значении краски для наруж­ных (внутренних) работ, обозначенный в таблице k₁ (k₂), равен 1 (0), а при неизвестном значении краски для внутренних (наружных) ра­бот k₂ (k₁) равен 0 (1).

6.5. Дана задача линейного программирования

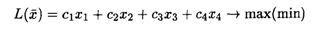
при ограничениях:

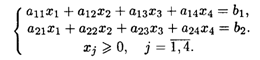
Решить задачу симплексным методом при стремлении це­левой функции к максимальному и минимальному значениям.

Значения коэффициентов целевой функции и системы ограничений

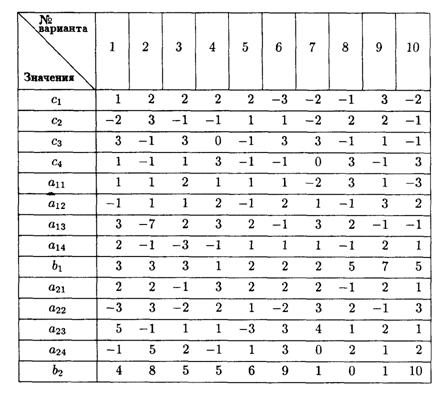
6.6. Составить математическую модель и решить задачу сим­плексным методом.

В производстве пользующихся спросом двух изделий, А и В, принимают участие 3 цеха фирмы. На изготовление одного изделия А 1-й цех затрачивает a₁ ч, 2-й цех — a₂ ч, 3-й цех — а₃ ч. На изготовление одного изделия В 1-й цех затрачивает d₁ ч, 2-й цех — d₂ ч, 3-й цех — d₃ ч. На производство обоих изделий 1-й цех может затратить не более b₁ ч, 2-й цех — не более b₂ ч, 3-й цех — не более b₃ ч.

От реализации одного изделия А фирма получает доход c₁ р., изделия В — c₂ р.

Определить максимальный доход от реализации всех изде­лий А и В.

Значения коэффициентов условия задачи

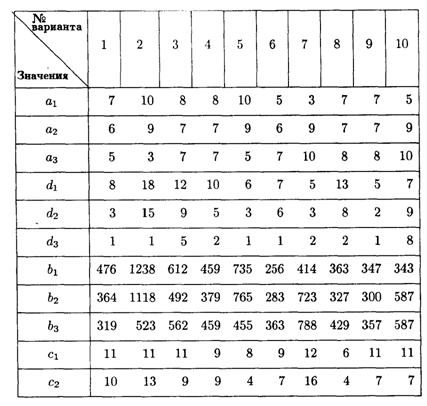
6.7. Дана исходная задача

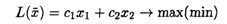
при ограничениях:

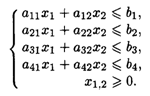
Составить математическую модель симметричной двойст­венной задачи. По решению двойственной или исходной зада­чи найти решение другой с использованием основных теорем двойственности.

Значения коэффициентов целевой функции и системы ограничений

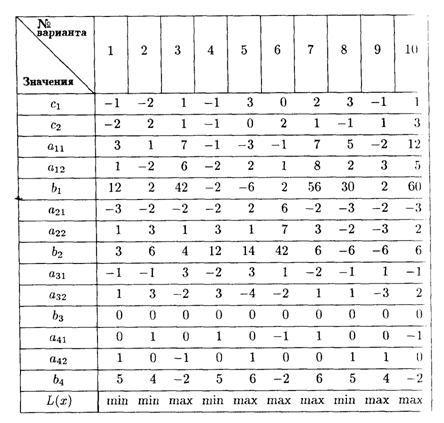
6.8. Дана исходная задача

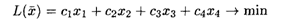
при ограничениях:

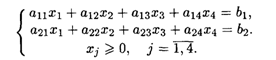
Составить математическую модель несимметричной двой­ственной задачи. По решению двойственной или исходной за­дачи найти решение другой с использованием основных теорем двойственности.

Значения коэффициентов целевой функции и системы ограничений

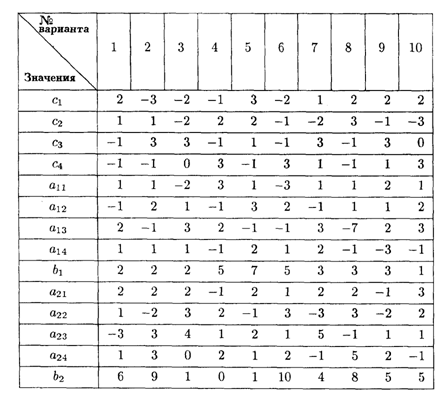
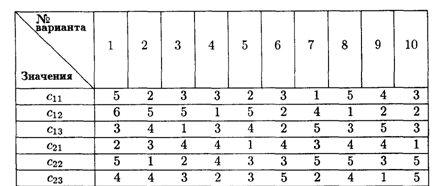
6.9. Решить транспортную задачу, заданную распределитель­ной таблицей

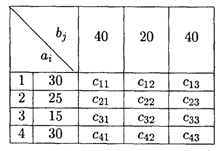
Значения коэффициентов распределительной таблицы

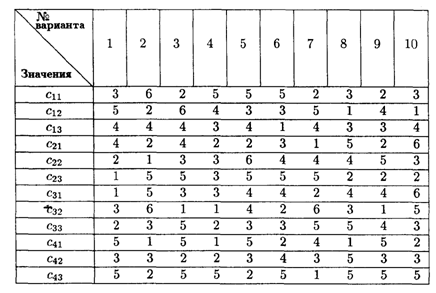
6.10. Решить транспортную задачу, заданную распредели­тельной таблицей

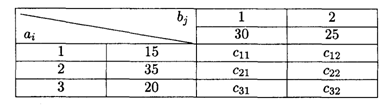
Значения коэффициентов распределительной таблицы

6.11. Составить математическую модель транспортной задачи и решить ее.

Фирма имеет три магазина розничной торговли, располо­женных в разных районах города (А, В, С). Поставки про­дукции в эти магазины осуществляются с двух складов D и Е, площади которых вмещают 30 и 25 т продукции соответ­ственно. В связи с возросшим покупательским спросом фирма планирует расширить площади магазинов, поэтому их потреб­ности в продукции с торговых складов составят 20, 35 и 15 т в день. Чтобы удовлетворить спрос на продукцию, предпола­гается строительство третьего склада, площади которого поз­волят хранить в нем 15 т продукции ежедневно. Руководство фирмы рассматривает два варианта его размещения. В таблице даны транспортные издержки, соответствующие перевозке продукции с двух существующих складов, и два варианта раз­мещения нового склада.

Оценить две транспортные модели и принять решение, ка­кой вариант размещения нового склада выгоднее. Предполага­ется, что остальные издержки сохраняют существующие зна­чения.

Значения коэффициентов

6.12. Дана задача линейного программирования

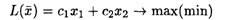
при ограничениях:

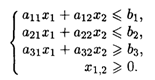
Графическим методом найти максимальное и минимальное целочисленные решения задач.

Решить задачу методом Гомори, принимая по своему усмотрению стремление целевой функции к максимальному или минимальному значениям.

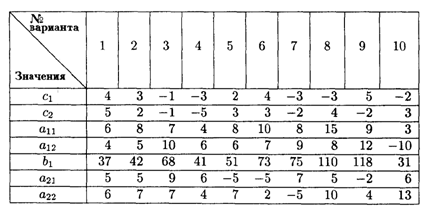
Значения коэффициентов целевой функции и системы ограничений

6.13. Дана задача параметрического программирования

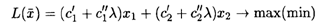
при ограничениях:

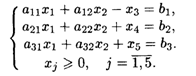
Решить задачу симплексным методом.

Значения коэффициентов целевой функции и системы ограничений

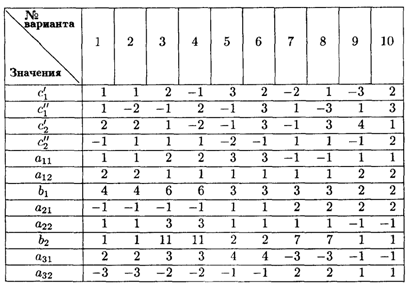
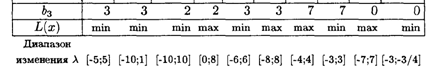
6.14. Решить транспортную параметрическую задачу, задан­ную распределительной таблицей

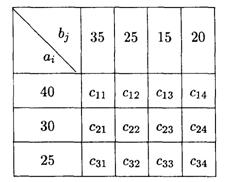
Значения коэффициентов распределительной таблицы

6.15. Решить задачу о назначении с использованием симплекс­ного метода.

Районная администрация финансирует 5 инвестиционных проектов, каждый из которых может быть осуществлен в тече­ние последующих трех лет. В связи с невозможностью финан­сирования в полном объеме определить, какие из инвестици­онных проектов, обеспечивающих максимально чистые приве­денные стоимости, могут быть осуществлены. Затраты, ожи­даемые чистые приведенные стоимости (ЧПС) и ограничения по финансированию проектов приведены ниже.

Таблица обозначений

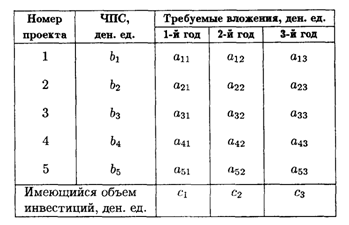
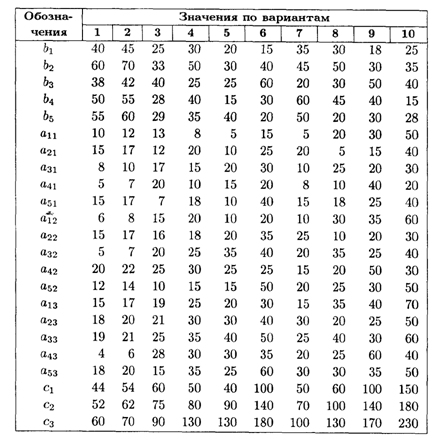
Таблица заданий по вариантам

Примечание. Задачу целесообразно решать на компьютере.

6.16. Решить задачу о назначениях.

В цехе предприятия имеется 5 универсальных станков, ко­торые могут выполнять 4 вида работ. Каждую работу еди­новременно может выполнять только один станок, и каждый станок можно загружать только одной работой.

В таблице даны затраты времени при выполнении станком определенной работы.

Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты вре­мени.

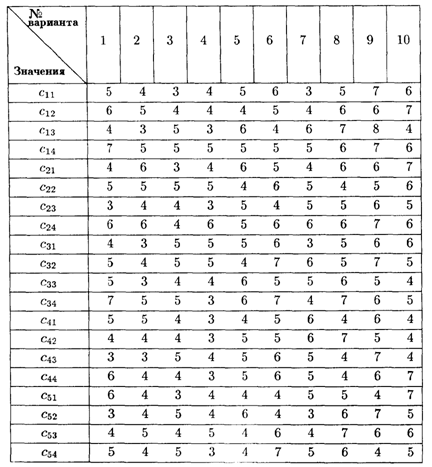
Значения коэффициентов распределительной таблицы

6.17. Решить задачу о назначениях.

Служба занятости имеет в наличии четыре вакантных мес­та по разным специальностям, на которые претендуют шесть человек. Проведено тестирование претендентов, результаты которого в виде баллов представлены в матрице

Распределить претендентов на вакантные места таким об­разом, чтобы на каждое место был назначен человек с наиболь­шим набранным по тестированию баллом.

Значения коэффициентов матрицы

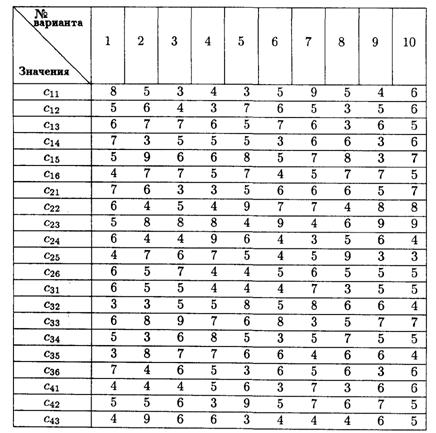
6.18. Дана задача линейного программирования с двумя целе­выми функциями

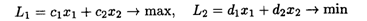
при ограничениях:

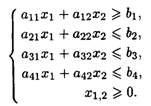
Составить математическую модель нахождения компро­миссного решения и найти его (решение математической мо­дели рекомендуется проводить на персональном компьютере).

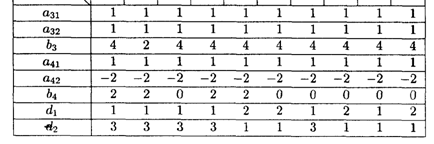
Значения коэффициентов целевой функции и системы ограничений

П7. Задания по теме "Нелинейное программирование"

7.1. Дана задача с линейной целевой функцией и нелинейной системой ограничений.

Используя графический метод, найти глобальные экстре­мумы функции, при этом с 1-го по 5-й вариант выполнения работ принять математическую модель задачи вида

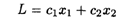
при ограничениях:

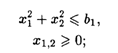
с 6-го по 10-й вариант — вида

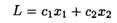
при ограничениях:

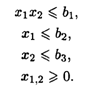
Значения коэффициентов целевых функций и систем ограничений

7.2. Дана задача с нелинейной целевой функцией и линейной системой ограничений.

Используя графический метод, найти глобальные экстре­мумы функции

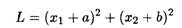
при ограничениях:

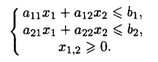
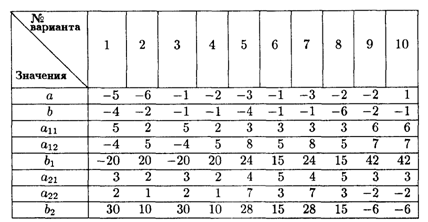
Значения коэффициентов целевой функции и системы ограничений

7.3. Дана задача с нелинейной целевой функцией и нелинейной системой ограничений.

Используя графический метод, найти глобальные экстре­мумы функции, при этом с 1-го по 5-й вариант выполнения работ принять математическую модель задачи вида

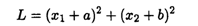
при ограничениях:

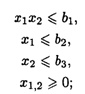
с 6-го по 10-й вариант — вида

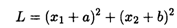
при ограничениях:

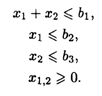
Значения коэффициентов целевой функции и системы ограничений

7.4. Решить задачу дробно-линейного программирования.

Для производства двух изделий A и В предприятие исполь­зует три типа технологического оборудования. Каждое из изде­лий должно пройти обработку на данном типе оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в таблице.

Оборудование 1-го и 3-го типов предприятие может исполь­зовать не менее b₁ и b₃ ч соответственно, оборудование 2-го типа — не более b₂ ч.

Определить, сколько изделий следует изготовить предпри­ятию, чтобы средняя себестоимость одного изделия была ми­нимальной.

Значения коэффициентов условия задачи

7.5. Дана задача нелинейного программирования

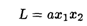
при ограничении

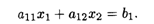
Найти условный экстремум с использованием метода множи­телей Лагранжа.

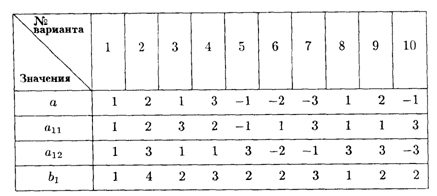
Значения коэффициентов целевой функции и системы ограничений

П8. Задания по теме "Динамическое программирование"

8.1. Определить оптимальный цикл замены оборудования при следующих исходных данных: S(t) = 0, f(t) = r(t) — u(t).

Значения коэффициентов условия задачи

8.2. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, при­надлежащих фирме.

Для модернизации предприятий совет директоров инвести­рует средства в объеме 250 млн р. с дискретностью 50 млн р. Прирост выпуска продукции зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таб­лице.

Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска про­дукции, причем на одно предприятие можно осуществить толь­ко одну инвестицию.

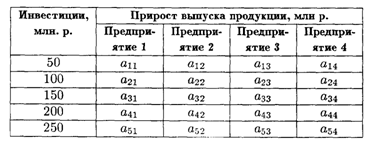
Значения коэффициентов условия задачи

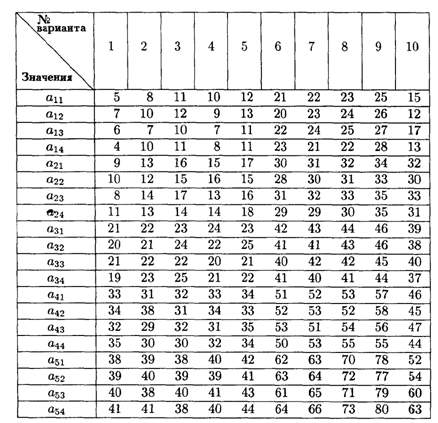
8.3. В трех районах города предприниматель планирует стро­ительство пользующихся спросом одинаковых по площади ми­ни-магазинов "Продукты". Известны места, в которых их мож­но построить. Подсчитаны затраты на их строительство и экс­плуатацию.

Необходимо так разместить мини-магазины, чтобы затра­ты на их строительство и эксплуатацию были минимальные.

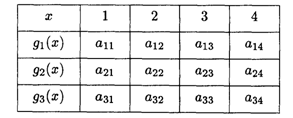
Значения коэффициентов условия задачи

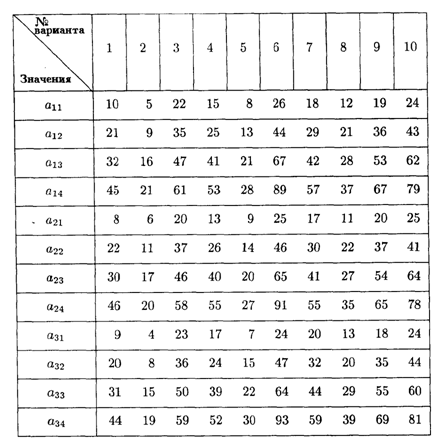
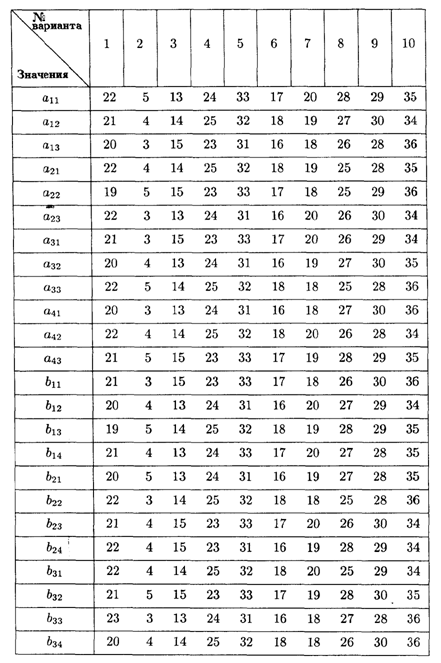
8.4. Требуется проложить трубопровод на дачном массиве между двумя пунктами А и В таким образом, чтобы затра­ты на проведение работ (в тыс. р.) были минимальные.

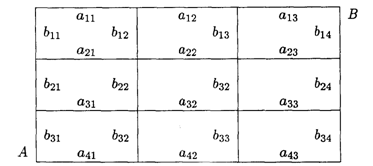
Значения коэффициентов условия задачи

П9. Задания по теме "Сетевые модели"

9.1. Районной администрацией принято решение о газифика­ции одного из небольших сел района, имеющего 10 жилых до­мов.

Расположение домов указано на рис. 9.1. Числа в кружках обозначают условный номер дома. Узел 11 является газопонижающей станцией.

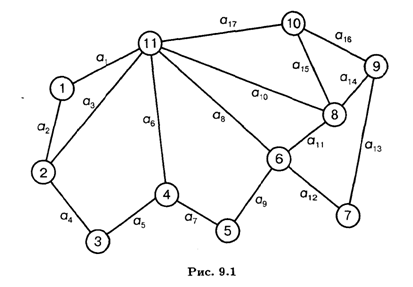
Разработать такой план газификации села, чтобы общая длина трубопроводов была наименьшей.

Значения коэффициентов условия задачи

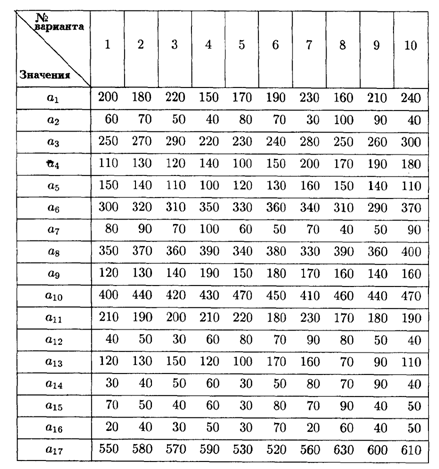
9.2. Транспортному предприятию требуется перевезти груз из пункта 1 в пункт 14. На рис. 9.2 показана сеть до­рог и стоимость перевозки единицы груза между отдельными пунктами.

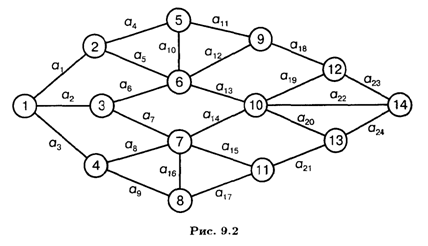
Определить маршрут доставки груза, которому соответ­ствуют наименьшие затраты.

Значения коэффициентов условия задачи

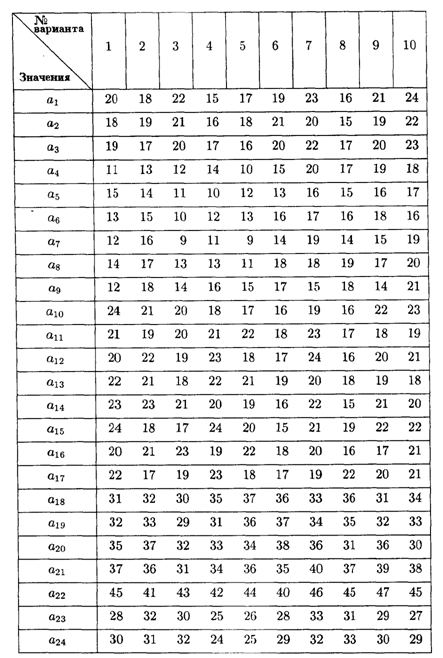
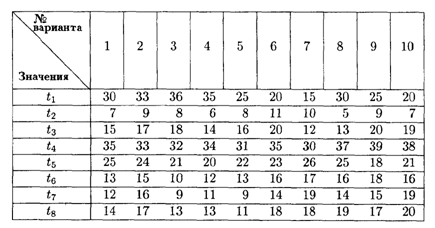
9.3. Составить сетевой график выполнения работ и рассчитать временные параметры по данным, представленным в таблице.

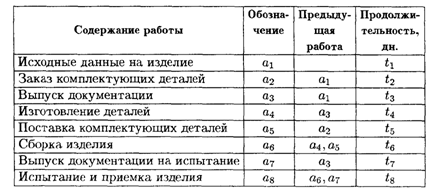
Значения коэффициентов условия задачи

9.4. Постройте график работ, определите критический путь и стоимость работ до сжатия. Найдите критический путь и минимальную стоимость работ после сжатия.

Значения коэффициентов условия задачи

П10. Задания по теме "Теория игр"

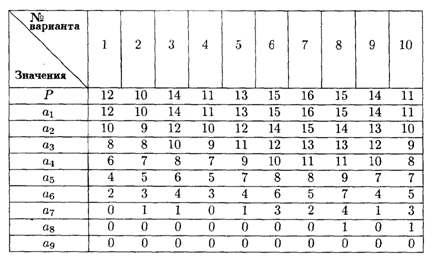
10.1. Найти оптимальные стратегии и цену игры, заданной платёжной матрицей. При этом с 1-го по 5-й вариант выпол­нения работ принять платежную матрицу вида

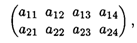
с 6-го по 10-й вариант — вида

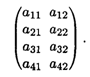
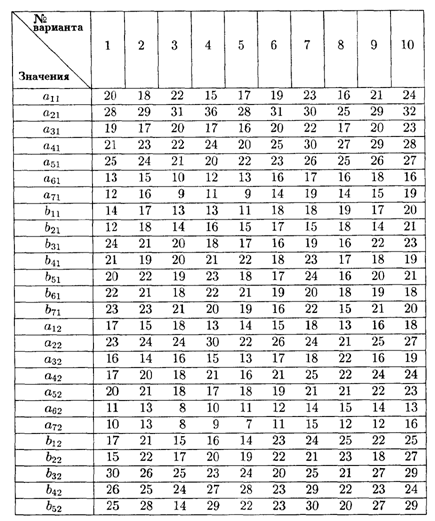
Значения коэффициентов платежных матриц

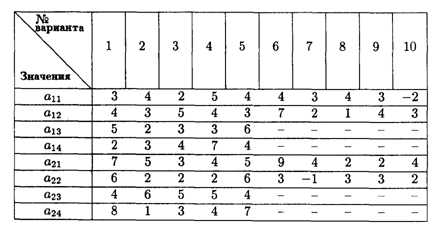
10.2. Торговая фирма разработала несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом конъ­юнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таб­лице.

1) Определить оптимальную стратегию фирмы в продаже товаров на ярмарке.

2) Если существует риск (вероятность реализации плана П₁ — b%, П₂ — с%, П₃ — d%),то какую стратегию фирме следует считать оптимальной?

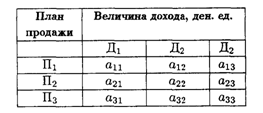
Значения коэффициентов условия задачи

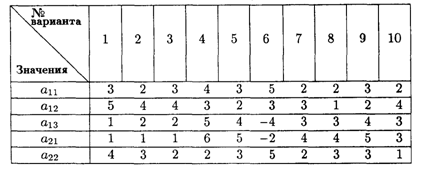
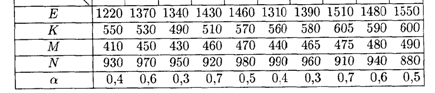
10.3. Фирма производит пользующиеся спросом детские пла­тья и костюмы, реализация которых зависит от состояния по­годы. Затраты фирмы в течение апреля-мая на единицу про­дукции составят: платья — А ден. ед., костюмы — В ден. ед. Цена реализации составит С ден. ед. и D ден. ед. соответствен­но.

По данным наблюдений за несколько предыдущих лет, фир­ма может реализовать в условиях теплой погоды Е шт. платьев и К шт. костюмов, при прохладной погоде — М шт. платьев и N шт. костюмов.

В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход.

Задачу решить графическим методом и с использованием критериев игр с природой, приняв степень оптимизма α, ука­занную в таблице.

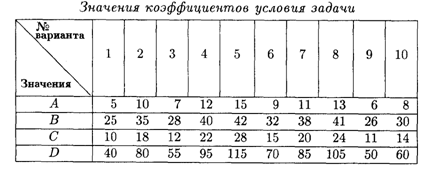
10.4. Решить задачу с использованием "дерева" решений.

Фирма планирует построить среднее или малое предпри­ятие по производству пользующейся спросом продукции. Ре­шение о строительстве определяется будущим спросом на про­дукцию, которую предполагается выпускать на планируемом предприятии.

Строительство среднего предприятия экономически оправ­данно при высоком спросе, но можно построить малое пред­приятие и через 2 года его расширить.

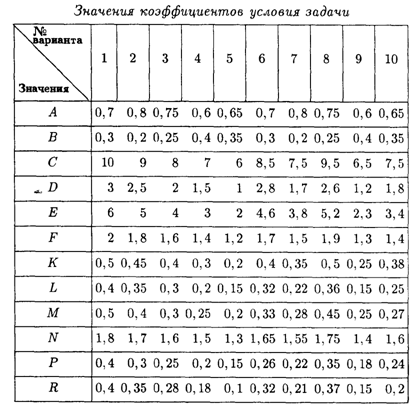
Фирма рассматривает данную задачу на десятилетний пе­риод. Анализ рыночной ситуации, проведенный службой мар­кетинга, показывает, что вероятности высокого и низкого уров­ней спроса составляют А и В соответственно.

Строительство среднего предприятия составит С млн р., малого — D млн р. Затраты на расширение малого предприя­тия оцениваются в Е млн р.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

• среднее предприятие при высоком (низком) спросе — F(K) млн р.;

• малое предприятие при низком спросе — L млн р.;

• малое предприятие при высоком спросе — М млн р.;

• расширенное предприятие при высоком (низком) спросе дает N(P) млн р.;

• малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R млн р. за остальные 8 лет.

Определить оптимальную стратегию фирмы в строитель­стве предприятий по выпуску продукции.

П11. Задания по теме "Система массового обслуживания"

11.1. Контроль готовой продукции фирмы осуществляют А контролеров. Если изделие поступает на контроль, когда все контролеры заняты проверкой готовых изделий, то оно остает­ся непроверенным. Среднее число изделий, выпускаемых фир­мой, составляет В изд./ ч. Среднее время на проверку одного изделия — С мин.

Определить вероятность того, что изделие пройдет провер­ку, насколько загружены контролеры и сколько их необходимо поставить, чтобы Р*_обс ≥ D.

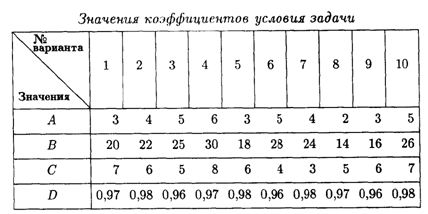
11.2. Приходная касса городского района с временем работы А часов в день проводит прием от населения коммунальных услуг и различных платежей в среднем от В человек в день.

В приходной кассе работают С операторов-кассиров. Сред­няя продолжительность обслуживания одного клиента состав­ляет D мин.

Определить характеристики работы приходной кассы как объекта СМО.

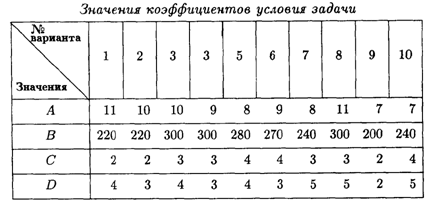
11.3. На АЗС установлено А колонок для выдачи бензина. Око­ло станции находится площадка на В автомашин для ожи­дания заправки. На станцию прибывает в среднем С маш./ч. Среднее время заправки одной автомашины — D мин.

Определить вероятность отказа и среднюю длину очереди.

ОТВЕТЫ К УПРАЖНЕНИЯМ

Глава 1

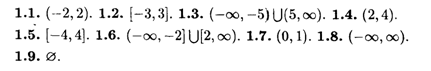
Глава 2

Глава 3

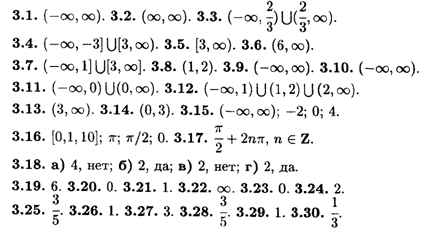
Глава 4

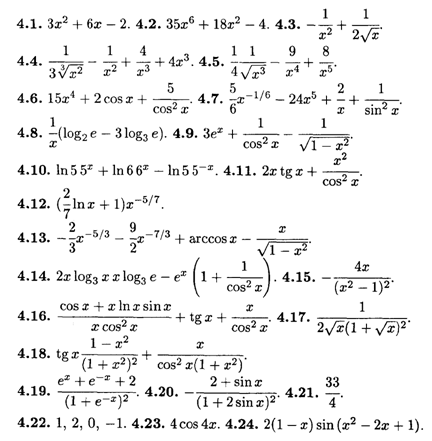
Глава 5

Глава 6

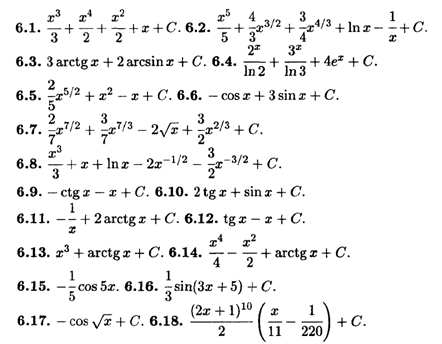
Глава 7

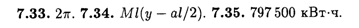
Глава 8

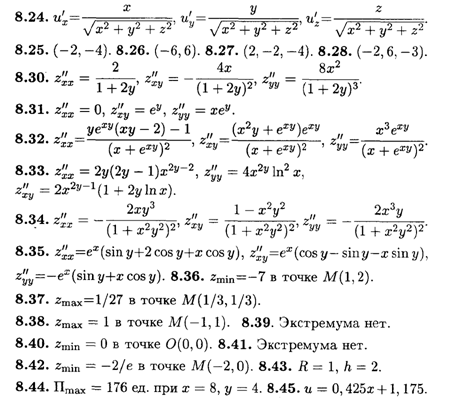
Глава 9

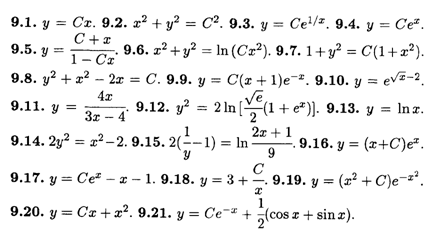
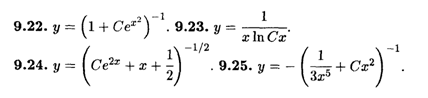
Глава 10

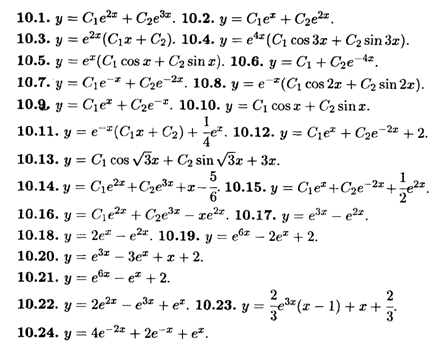
Глава 11

Глава 12

Глава 13

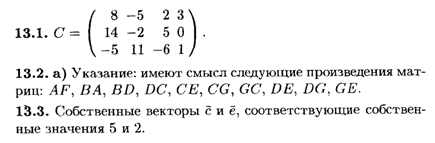
Глава 14

Глава 15

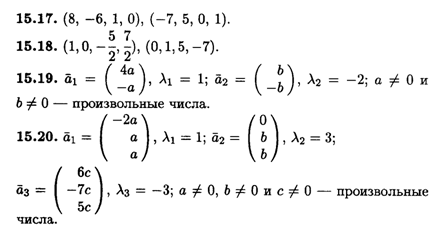
Глава 16

Глава 17

Глава 18

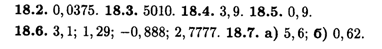
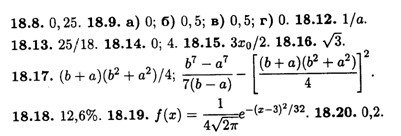
Глава 20

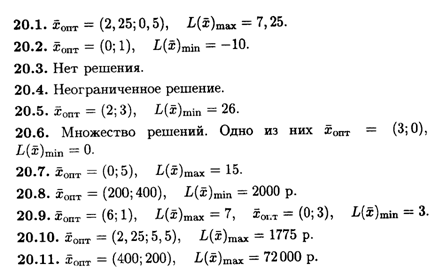
Глава 21

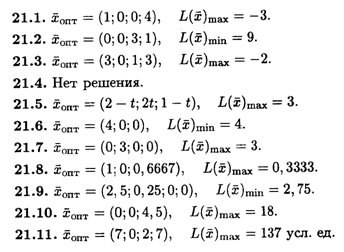
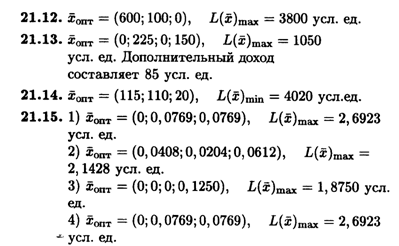
Глава 22

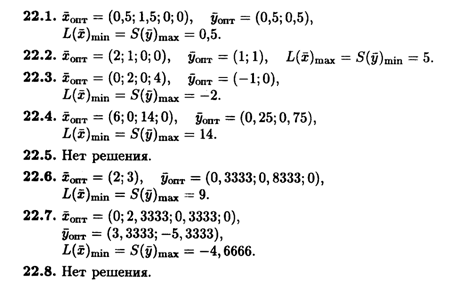
Глава 23

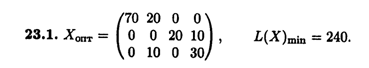
Глава 24

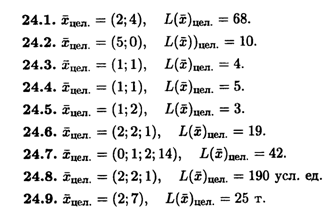
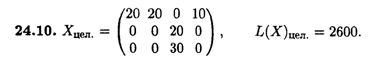
Глава 25

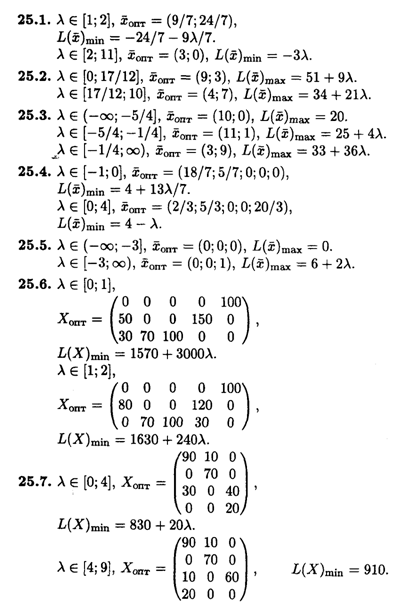
Глава 26

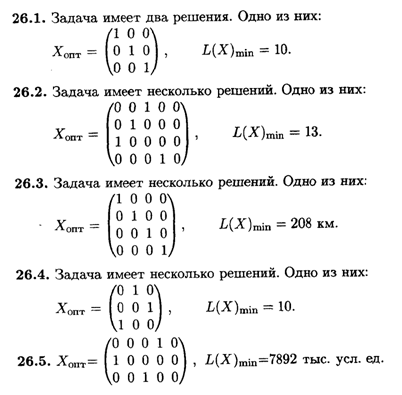
Глава 27

Глава 28

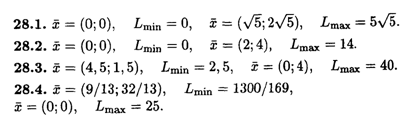
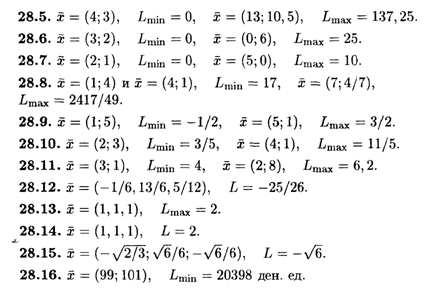
Глава 29

Глава 30

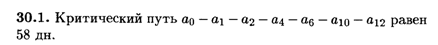
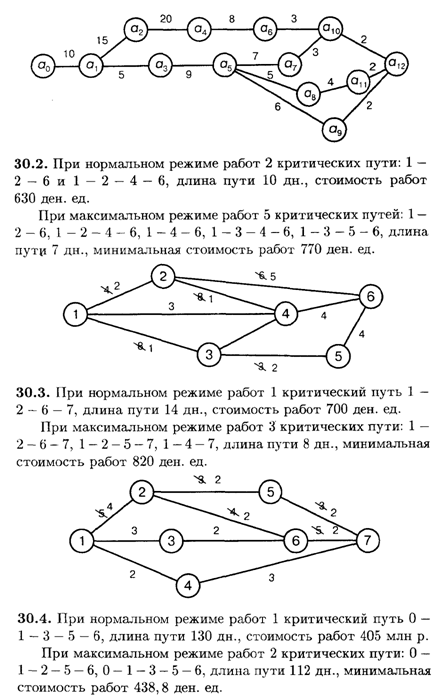
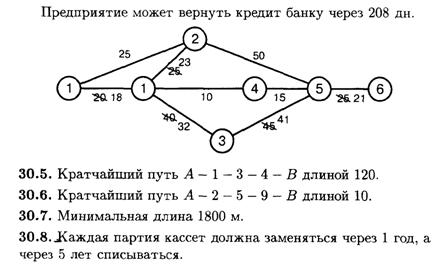
Глава 31

Глава 32

ПРИЛОЖЕНИЕ

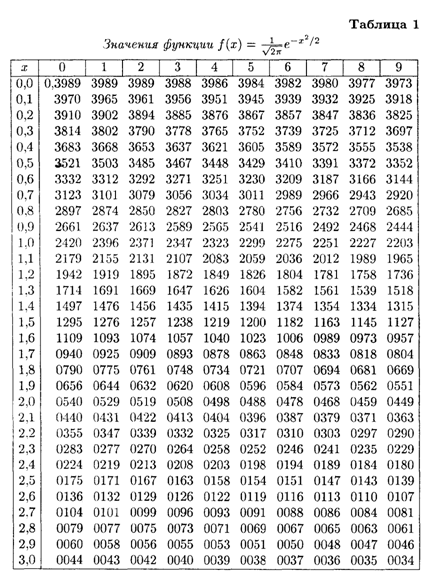
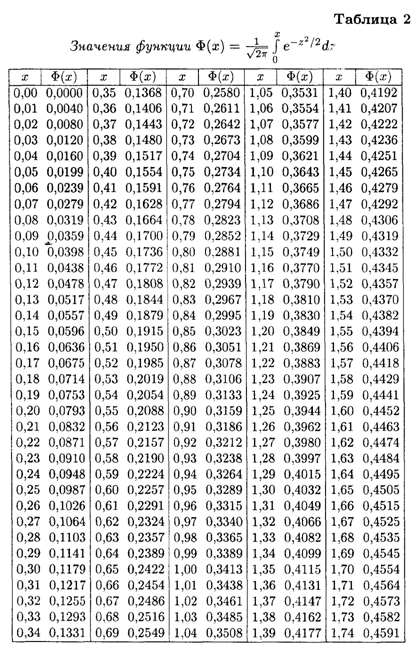
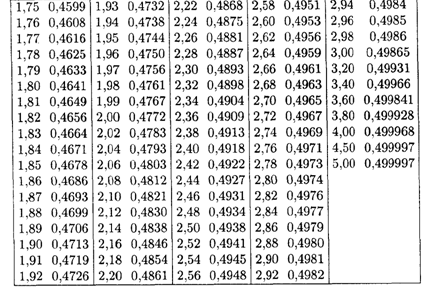
ЛИТЕРАТУРА

[1] И.Л. Акулич. Математическое программирование в примерах и за­дачах. М., "Высшая школа", 1986.

[2] В.А. Бабайцев, А.В. Браилов, А.С. Солодовников. Математика в экономике. Часть 5. Руководство к решению задач. Теория вероят­ностей. М., Финансовая академия при Правительстве РФ, 1999.

[3] М.И. Баканов, А.Д. Шеремет. Теория экономического анализа. — М., "Финансы и статистика", 1994.

[4] Н.П. Башарин. Начала финансовой математики. - М., "ИНФРА-М", 1995.

[5] В.Е. Гмурман. Теория вероятностей и математическая статисти­ка. — М., "Высшая школа", 1998.

[6] В.Е. Гмурман. Руководство по решению задач по теории вероятностей и математической статистике. М., "Высшая школа", 1998.

[7] Н.П. Кондраков. Эккаунтинг для менеджеров. — М., "Дело", 1998.

[8] М.С. Красс. Математика для экономических специальностей. — М., "ИНФРА-М", 1998.

[9] Л.Г. Лабскер, Л.О. Бабешко. Теория массового обслуживания в эко­номической сфере. — М., "ЮНИТИ", 1998.

[10] А.А. Первозванский, Т.Н. Первозванская. Финансовый рынок: расчет и риск. — М., "ИНФРА-М", 1994.

[11] Г.И. Фалин. Математический анализ рисков в страховании. — М., Российский Юридический Издательский Дом, 1994.

[12] В.В. Федосеев. Экономико-математические модели и методы в мар­кетинге. - М., "Финстатпром",1996.

[13] В.А. Чернов. Анализ коммерческого риска. — М., "Финансы и ста­тистика", 1998.

[14] Е.М. Четыркин. Методы финансовых и коммерческих расчетов. — М., "ИНФРА-М", 1995.

[15] B.C. Шипачев. Высшая математика. — М., "Высшая школа", 1995.

[16] В. С. Шипачев. Задачи по высшей математике. — М., "Высшая шко­ла".

Содержание

ПРЕДИСЛОВИЕ........................................................................................................................................................................................................ 3

ВВЕДЕНИЕ................................................................................................................................................................................................................ 3

Раздел I. ОСНОВЫ МАТЕМАТИКИ....................................................................................................................................................................... 4

Часть 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ.............................................................................................................................................................. 4

Глава 1. МНОЖЕСТВА.......................................................................................................................................................................................... 4

1.1. Множества. Основные обозначения. Операции над множествами............................................................................................... 4

1.2. Вещественные числа и их свойства........................................................................................................................................................ 5

1.3. Числовая прямая (числовая ось) и множества на ней....................................................................................................................... 6

1.4. Грани числовых множеств........................................................................................................................................................................ 7

1.5. Абсолютная величина числа.................................................................................................................................................................... 8

Глава 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ................................................................................................................................................ 8

2.1. Числовые последовательности................................................................................................................................................................ 8

2.2 Применение в экономике.......................................................................................................................................................................... 12

Глава 3. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ............................................................................................................................................... 14

3.1. Понятие функции....................................................................................................................................................................................... 14

3.2. Предел функции......................................................................................................................................................................................... 18

3.3. Теоремы о пределах функций................................................................................................................................................................ 20

3.4. Два замечательных предела.................................................................................................................................................................. 21

3.5. Бесконечно малые и бесконечно большие функ