Определение эффективности использования трудовых и производственных ресурсов в системах массового обслуживания

Рассмотрим задачу с использованием СМО с отказами.

Пример 1. В ОТК цеха работают три контролера. Если де­таль поступает в ОТК, когда все контролеры заняты обслу­живанием ранее поступивших деталей, то она проходит не­проверенной. Среднее число деталей, поступающих в ОТК и течение часа, равно 24, среднее время, которое затрачивает один контролер на обслуживание одной детали, равно 5 мин. Определить вероятность того, что деталь пройдет ОТК не обслуженной, насколько загружены контролеры и сколько их необходимо поставить, чтобы Р*_обс ≥ 0,95 (* — заданное значение Р_обс).

Решение. По условию задачи λ = 24дет./ч = 0,4дет./мин, 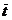_обс = 5 мин, тогда μ = 0,2, ρ = λ / μ = 2.

1. Вероятность простоя каналов обслуживания:

2. Вероятность отказа в обслуживании:

3. Вероятность обслуживания:

4. Среднее число занятых обслуживанием каналов:

5. Доля каналов, занятых обслуживанием:

6. Абсолютная пропускная способность:

При п = 3 Р_обс = 0,79 ≤ Р*_обс = 0,95. Произведя аналогич­ные расчеты для п = 4, получим

Так как Р_обс = 0,907 ≤ Р*_обс = 0,95, то, произведя расчеты для п = 5, получим

Ответ. Вероятность того, что при п = 3 деталь прой­дет ОТК необслуженной, составляет 21%, и контролеры будут заняты обслуживанием на 53%.

Чтобы обеспечить вероятность обслуживания более 95%, необходимо не менее пяти контролеров.

Рассмотрим задачу с использованием СМО с неограничен­ным ожиданием.

Пример 2. Сберкасса имеет трех контролеров-кассиров (п = 3) для обслуживания вкладчиков. Поток вкладчиков посту­пает в сберкассу с интенсивностью λ = 30 чел./ч. Средняя продолжительность обслуживания контролером-кассиром од­ного вкладчика 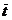_обс = 3 мин.

Определить характеристики сберкассы как объекта СМО.

Решение. Интенсивность потока обслуживания μ = 1/ 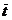_обс = 1/3 = 0,333, интенсивность нагрузки ρ = 1,5.

1. Вероятность простоя контролеров-кассиров в течение рабочего дня:

2. Вероятность застать всех контролеров-кассиров заняты­ми:

3. Вероятность очереди:

4. Среднее число заявок в очереди:

5. Среднее время ожидания заявки в очереди:

6. Среднее время пребывания заявки в СМО:

7. Среднее число свободных каналов:

8. Коэффициент занятости каналов обслуживания:

9. Среднее число посетителей в сберкассе:

Ответ. Вероятность простоя контролеров-кассиров рав­на 21% рабочего времени, вероятность посетителю оказаться в очереди составляет 11,8%, среднее число посетителей в очереди 0,236 чел., среднее время ожидания посетителями обслужива­ния 0,472 мин.

Рассмотрим задачу с применением СМО с ожиданием и с ограниченной длиной очереди.

Пример 3. Магазин получает ранние овощи из пригородных теплиц. Автомобили с грузом прибывают в разное время с ин­тенсивностью λ = 6 машин в день. Подсобные помещения и оборудование для подготовки овощей к продаже позволяют об­рабатывать и хранить товар, привезенный двумя автомаши­нами (m = 2). В магазине работают три фасовщика (n = 3), каждый из которых в среднем может обрабатывать товар с од­ной машины в течение 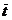_обс = 4 ч. Продолжительность рабочего дня при сменной работе составляет 12 ч.

Определить, какова должна быть емкость подсобных по­мещений, чтобы вероятность полной обработки товаров была Р*_обc ≥ 0,97.

Решение. Определим интенсивность загрузки фасовщи­ков:

1. Найдем вероятность простоя фасовщиков при отсут­ствии машин (заявок):

причем 0! = 1,0.

2. Вероятность отказа в обслуживании:

3. Вероятность обслуживания:

Так как Р_обс = 0,925 < Р*_обс = 0,97, произведем аналогич­ные вычисления для т = 3, получим

Так как Р_обс = 0,952 < Р*_обс = 0,97, примем т = 4.

Для этого случая

0,972 > 0,97, емкость подсобных помещений необходимо увели­чить до т = 4.

Для достижения заданной вероятности обслуживания мож­но увеличивать число фасовщиков, проводя последовательно вычисления СМО для п = 4, 5 и т.д. Задачу можно решить, увеличивая емкость подсобных помещений, число фасовщиков, уменьшая время обработки товаров.

Найдем остальные параметры СМО для рассчитанного слу­чая при P₀ = 0,12, Р_отк = 0,028, Р_обc = 0,972.

4. Абсолютная пропускная способность:

5. Среднее число занятых обслуживанием каналов (фасов­щиков) :

6. Среднее число заявок в очереди:

7. Среднее время ожидания обслуживания:

8. Среднее число машин в магазине:

9. Среднее время пребывания машины в магазине:

Ответ. Емкость подсобных помещений магазина должна вмещать товар, привезенный 4 автомашинами (m = 4), при этом вероятность полной обработки товара будет Р_обc = 0,972.

УПРАЖНЕНИЯ

Решить следующие задачи в предположении, что поток посту­пающих заявок является простейшим и длительность обслужи­вания одной заявки распределена по показательному закону.

32.1. Дежурный по администрации города имеет пять телефо­нов. Телефонные звонки поступают с интенсивностью 90 за­явок в час, средняя продолжительность разговора составляет 2 мин.

Определить показатели дежурного администратора как объек­та СМО.

32.2. На стоянке автомобилей возле магазина имеются 3 места, каждое из которых отводится под один автомобиль. Автомоби­ли прибывают на стоянку с интенсивностью 20 автомобилей в час. Продолжительность пребывания автомобилей на стоянке составляет в среднем 15 мин. Стоянка на проезжей части не разрешается.

Определить среднее количество мест, не занятых автомобиля­ми, и вероятность того, что прибывший автомобиль не найдет на стоянке свободного места.

32.3. АТС предприятия обеспечивает не более 5 переговоров одновременно. Средняя продолжительность разговоров состав­ляет 1 мин. На станцию поступает в среднем 10 вызовов в с.

Определить характеристики АТС как объекта СМО.

32.4. В грузовой речной порт поступает в среднем 6 сухогру­зов в сутки. В порту имеются 3 крана, каждый из которых обслуживает 1 сухогруз в среднем за 8 ч. Краны работают круглосуточно.

Определить характеристики работы порта как объекта СМО и в случае необходимости дать рекомендации по улучшению его работы.

32.5. В службе "Скорой помощи" поселка круглосуточно де­журят 3 диспетчера, обслуживающие 3 телефонных аппара­та. Если заявка на вызов врача к больному поступает, когда диспетчеры заняты, то абонент получает отказ. Поток заявок составляет 4 вызова в минуту. Оформление заявки длится в среднем 1,5 мин.

Определить основные показатели работы службы "Скорой по­мощи" как объекта СМО и рассчитать, сколько потребуется телефонных аппаратов, чтобы удовлетворить не менее 90% по­ступающих вызовов врачей.

32.6. Салон-парикмахерская имеет 4 мастера. Входящий по­ток посетителей имеет интенсивность 5 человек в час. Среднее время обслуживания одного клиента составляет 40 мин.

Определить среднюю длину очереди на обслуживание, считая ее неограниченной.

32.7. На автозаправочной станции установлены 2 колонки для выдачи бензина. Около станции находится площадка на 2 ав­томашины для ожидания заправки. На станцию прибывает в среднем одна машина в 3 мин. Среднее время обслуживания одной машины составляет 2 мин.

Определить характеристики работы автозаправочной станции как объекта СМО.

32.8. На вокзале в мастерской бытового обслуживания рабо­тают три мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит из мастерской, не ожидая обслуживания. Среднее число клиентов, обращающихся в мас­терскую за 1 ч, равно 20. Среднее время, которое затрачивает мастер на обслуживание одного клиента, равно 6 мин.

Определить вероятность того, что клиент получит отказ, бу­дет обслужен, а также среднее число клиентов, обслуживаемых мастерской в течение 1 ч, и среднее число занятых мастеров.

32.9. АТС поселка обеспечивает не более 5 переговоров од­новременно. Время переговоров в среднем составляет около 3 мин. Вызовы на станцию поступают в среднем через 2 мин.

Определить вероятность того, что заявка получит отказ, сред­нее число занятых каналов, абсолютную пропускную способ­ность АТС.

32.10. На автозаправочной станции (АЗС) имеются 3 колонки. Площадка при станции, на которой машины ожидают заправ­ку, может вместить не более одной машины, и если она занята, то очередная машина, прибывшая к станции, в очередь не ста­новится, а проезжает на соседнюю станцию. В среднем маши­ны прибывают на станцию каждые 2 мин. Процесс заправки одной машины продолжается в среднем 2,5 мин.

Определить вероятность отказа, абсолютную пропускную спо­собность АЗС, среднее число машин, ожидающих заправку, среднее время ожидания машины в очереди, среднее время пре­бывания машины на АЗС (включая обслуживание).

32.11. В небольшом магазине покупателей обслуживают два продавца. Среднее время обслуживания одного покупателя — 4 мин. Интенсивность потока покупателей — 3 человека в ми­нуту. Вместимость магазина такова, что одновременно в нем в очереди могут находиться не более 5 человек. Покупатель, при­шедший в переполненный магазин, когда в очереди уже стоят 5 человек, не ждет снаружи и уходит.

Определить вероятность того, что пришедший в магазин по­купатель покинет магазин необслуженным.

32.12. Железнодорожную станцию дачного поселка обслужи­вает касса с двумя окнами. В выходные дни, когда население активно пользуется железной дорогой, интенсивность потока пассажиров составляет 0,9 чел./мин. Кассир затрачивает на обслуживание пассажира в среднем 2 мин.

Определить среднее число пассажиров у кассы и среднее время, затрачиваемое пассажиром на приобретение билета.