Числовые характеристики непрерывных случайных величин

Определения числовых характеристик дискретных случай­ных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (18.5) и (18.10) берутся их интегральные аналоги.

Определение 4. Математическим ожиданием непрерывной случайной величины X, возможные значения которой находят­ся на отрезке [а, b], называется определенный интеграл:

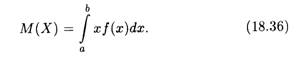
В том случае, когда возможные значения случайной вели­чины Х заполняют всю ось Ох, пределы интегрирования а и b бесконечны: а = - , b = . Возможны также случаи, ког­да один из пределов интегрирования бесконечен (возможные значения Х лежат на полупрямой).

Определение 5. Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения:

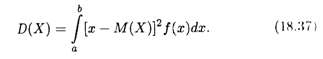
Все сказанное выше о случаях бесконечных пределов интегрирования остается справедливым и для дисперсии.

Среднее квадратичекое отклоенние непрерывной случайной величины определяется, как и прежде, по формуле (18.15):

σ(Х) = .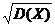

Для вычисления дисперсии употребляется более удобная фор­мула, которая выводится из (18.37):

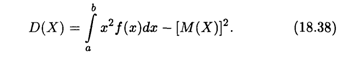
Пример 4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной плотностью распределения на отрезке [0, 1]:

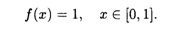
Решение. Согласно формулам (18.36), (18.38) и (18.15) по­следовательно вычисляем искомые величины:

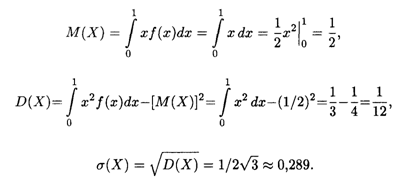
Пример 5. Найти основные числовые характеристики непре­рывной случайной величины X, заданной функцией распреде­ления на положительной полуоси Ох:

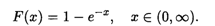
Решение. Найдем сначала плотность распределения:

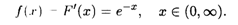
Затем, как и в предыдущем примере, вычисляем соответствуцющие интегралы; при их вычислении применяем правило интегрирования по частям для определенного интеграла. В итоге получаем искомые величины:

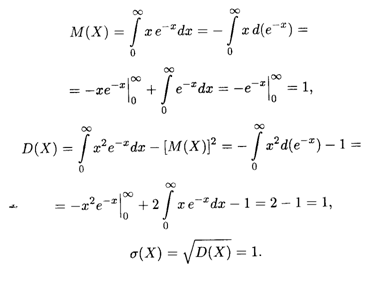
Основные распределения непрерывных случайных величин

Равномерное распределение

Определение 1. Распределение вероятностей называется рав­номерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.

Пусть на интервале (a, b) плотность распределения являет­ся постоянной величиной: f(x) = С. Определим значение С из условия (18.35):

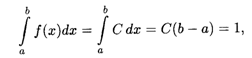
откуда получаем, что f(x) = С = 1/(b - а). Значит, искомая плотность равномерного распределения дается формулой

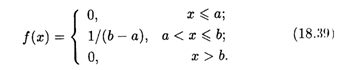
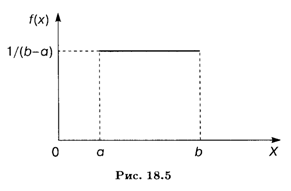
График плотности равномерного распределения указан на рис. 18.5.

Пример 1. Найти среднеквадратическое отклонение случай­ной величины X, распределенной равномерно на интерва­ле (1, 5).

Решение. Согласно формуле (18.39), плотность распреде­ления указанной случайной величины является ненулевой и равна 0,25 на интервале (1, 5). По формулам (18.36) и (18.38) последовательно вычисляем:

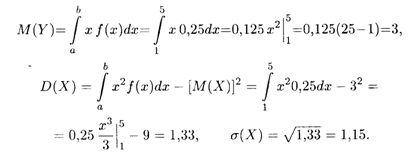
Пример 2. Радиус круга измерен приближенно на интервале (а, b). Полагая, что радиус является случайной величиной X, распределенной равномерно в этом интервале, найти матема­тическое ожидание и дисперсию площади круга.

Решение. Площадь круга также является случайной ве­личиной, вычисляемой по формуле Y = πX²; она имеет то же равномерное распределение, что и случайная величина X. По формулам (18.36) и (18.38) получаем

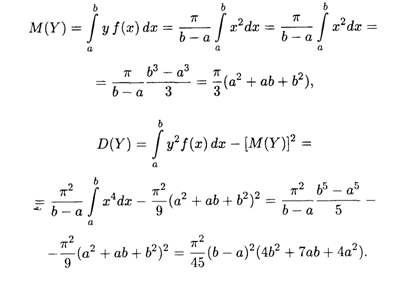
Нормальное распределение

Определение 2. Общим нормальным распределением вероят­ностей непрерывной случайной величины Х называется рас­пределение с плотностью

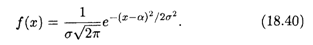
Нормальное распределение задается двумя параметрами: а и σ. Согласно определениям математического ожидания и дисперсии (формулы (18.36) и (18.38)), после выполнения соответствующих интегрирований можно вывести, что для нор­мального распределения справедливы формулы

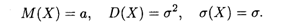
Определение 3. Нормальное распределение с параметрами а = 0 и σ = 1 называется нормированным; его плотность равна

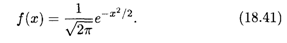
Рассмотрим функцию нормального распределения как пер­вообразную плотности распределения вероятностей. Для слу­чая нормированного нормального распределения (18.41) она, согласно формуле (18.34), имеет вид

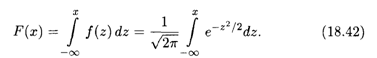
Поскольку функция (18.41) является четной, то неопределен­ный интеграл от нее является нечетной функцией, и потому вместо функции распределения (18.42) используется функция Лапласа (см. п. 17.5)

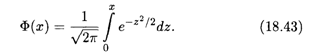
Функции (18.41) и (18.43) табулированы (см. Приложение).

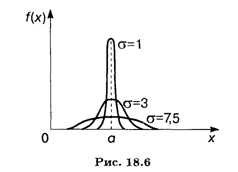
График плотности нормального распределения (18.40) для разных значений а показан на рис. 18.6.

Определение 4. Модой М_о(Х) называется возможное значе­ние случайной величины X, при котором плотность распреде­ления имеет максимум.

Определение 5. Медианой М_е(Х) называется такое возмож­ное значение случайной величины X, что вертикальная пря­мая х = M_e(X) делит пополам площадь, ограниченную кривой плотности распределения.

Нетрудно видеть, что график плотности нормального рас­пределения симметричен относительно прямой х = а, и потому и мода и медиана в данном случае совпадают с математичес­ким ожиданием:

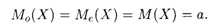
Пусть случайная величина Х задана плотностью нормаль­ного распределения (18.40), тогда вероятность того, что Х при­мет значение на интервале (α, β), согласно формуле (18.33), равна

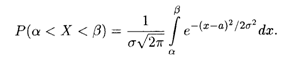
Преобразование этой формулы путем введения новой перемен­ной интегрирования z = (х - а)/σ приводит к удобной вычис­лительной формуле:

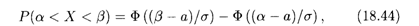
где Ф — функция Лапласа, определенная по формуле (18.43).

Пример 3. Случайная величина распределена по нормальному закону с математическим ожиданием и средним квадратическим отклонением, соответственно равными 10 и 5. Найти ве­роятность того, что Х примет значение на интервале (20, 30).

Решение. Воспользуемся формулой (18.44). По условию а = 10, σ = 5, α = 20 и β = 30. Следовательно,

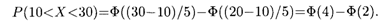
По табл. 2 Приложения находим соответствующие значения функции Лапласа и окончательно получаем

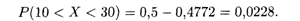
Пример 4. Магазин производит продажу мужских костюмов. По данным статистики, распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, соответственно равными 48 и 2. Опре­делить процент спроса на 50-й размер при условии разброса значений этой величины в интервале (49, 51).

Решение. По условию задачи а = 48, σ = 2, α = 49, β = 51. Используя формулу (18.44), получаем, что вероятность спроса на 50-й размер в заданном интервале равна

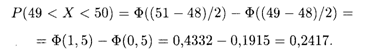
Следовательно, спрос на 50-й размер костюмов составит около 24%, и магазину нужно предусмотреть это в общем объеме закупки.

Асимметрия и эксцесс

В прикладных задачах, например в математической ста­тистике, при теоретическом изучении эмпирических распре­делений, отличающихся от нормального распределения, воз­никает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.

Определение 6. Асимметрией теоретического распределения называется отношение центрального момента третьего поряд­ка к кубу среднего квадратического отклонения:

Определение 7. Эксцессом теоретического распределения на­зывается величина, определяемая равенством

где μ₄ — центральный момент четвертого порядка.

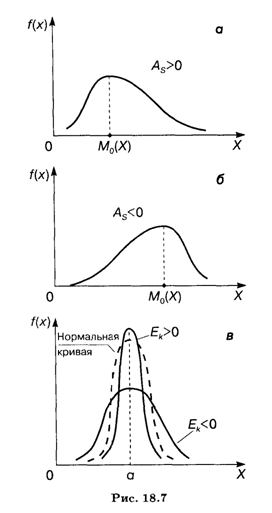
Для нормального распределения A_s = Е_k = 0. При отклоне­нии от нормального распределения асимметрия положительна, если "длинная" и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствую­щей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 18.7, а, б).

Эксцесс характеризует "крутизну" подъема кривой распре­деления по сравнению с нормальной кривой: если эксцесс поло­жителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину (рис. 18.7, в).

Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дис­персии для нормального и теоретического распределений.

Пример 5. Пусть дискретная случайная величина Х задана законом следующего распределения:

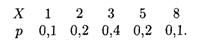
Найти асимметрию и эксцесс теоретического распределения.

Решение. Найдем сначала математическое ожидание слу­чайной величины:

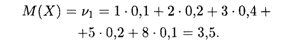
Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение (см. фор­мулы (18.27)-(18.31)):

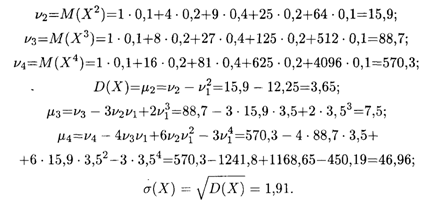
Теперь по формулам (18.45) и (18.46) находим искомые вели­чины:

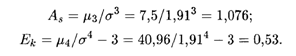
В данном случае "длинная" часть кривой распределения рас­положена справа от моды, причем сама кривая является не­сколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.