Часть 3. элементы линейной алгебры
Глава 12. ВЕКТОРЫ
Векторное пространство
Понятие и основные свойства вектора
Приведем обобщение понятия вектора на n-мерный случай.
Определение 1. Любой упорядоченный набор из п действительных чисел a1, a2, ..., ап называется п-мерным вектором  ; при этом числа, составляющие упомянутый набор, называются координатами (компонентами) вектора
; при этом числа, составляющие упомянутый набор, называются координатами (компонентами) вектора  .
.
Определение 2.Совокупность всех n-мерных векторов называется n-мерным векторным пространством Rn.
Координаты n-мерного вектора можно расположить либо в строку:
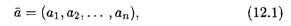
либо в столбец:
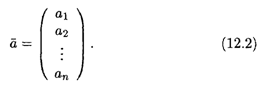
Запись вида (12.1) называется вектором-строкой, а вида (12.2) — вектором-столбцом.
Определение 3. Два вектора с одним и тем же числом координат
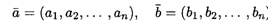
называются равными, если их соответствующие координаты равны, т.е.
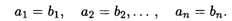
Определение 4. Вектор, все координаты которого равны нулю, называется нулевым вектором
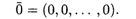
Операции над векторами
Пусть векторы и принадлежат n-мерному векторному пространству Rn:
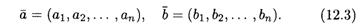
Будем называть суммой векторов  и
и 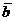 вектор
вектор 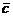 , координаты которого равны суммам соответствующих координат этих векторов:
, координаты которого равны суммам соответствующих координат этих векторов:
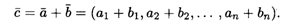
Пусть λ — любое действительное число. Произведением вектора  на число λ будем называть вектор, координаты которого получаются умножением соответствующих координат вектора
на число λ будем называть вектор, координаты которого получаются умножением соответствующих координат вектора  на это число:
на это число:
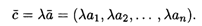
Из введенных таким образом операций над векторами вытекают следующие свойства этих операций. Пусть  ,
,  и
и  — произвольные векторы n-мерного векторного пространства. Тогда:
— произвольные векторы n-мерного векторного пространства. Тогда:
1)  +
+ 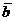 =
= 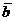 +
+  — переместительное свойство;
— переместительное свойство;
2) (  +
+ 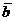 ) +
) + 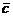 =
=  + (
+ ( 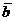 +
+ 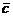 ) — сочетательное свойство;
) — сочетательное свойство;
3) λ(  +
+ 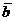 ) = λ
) = λ  + λ
+ λ 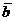 , где λ — действительное число;
, где λ — действительное число;
4) (λ + μ)  = λ
= λ  + μ
+ μ  , где λ и μ — действительные числа;
, где λ и μ — действительные числа;
5) λ(μ  ) = (λμ)
) = (λμ)  , где λ и μ — действительные числа;
, где λ и μ — действительные числа;
6)  +
+ 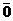 =
=  ;
;
7) для любого вектора  существует такой вектор -
существует такой вектор -  , что -
, что -  = (-1)
= (-1)  ,
,  + (-
+ (-  ) =
) = 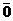 ;
;
8) 0  =
= 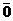 для любого вектора
для любого вектора  .
.
Скалярное произведение векторов
Определение 5. Скалярным произведением векторов (12.3) называется число, состоящее из суммы произведений соответствующих координат этих векторов:
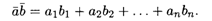
Как мы видим, формально такое определение скалярного произведения двух векторов согласуется с аналогичным определением двух- и трехмерных векторов. Из данного определения следуют основные свойства скалярного произведения векторов:
1) 
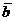 =
= 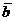
 ;
;
2) (λ  )
) 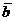 =
=  (λ
(λ 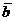 ) = λ(
) = λ( 
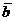 ), где λ — действительное число;
), где λ — действительное число;
3)  (
( 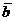 +
+ 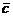 ) =
) = 
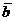 +
+ 
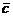 ;
;
4) 
 > 0, если
> 0, если  ≠
≠ 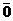 , и
, и 
 = 0, если
= 0, если  =
= 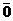 .
.
Введем понятие модуля вектора (его длины) и угла между векторами в виде обобщения на случай п > 3.
Определение 6. Для векторов из n-мерного векторного пространства модуль вектора  и угол φ между двумя ненулевыми векторами
и угол φ между двумя ненулевыми векторами  и
и 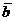 определяются по формулам:
определяются по формулам:
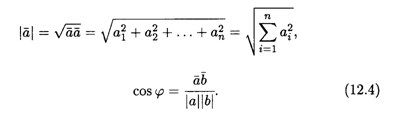
Укажем одно важное свойство векторов. Векторы  и
и 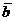 будем называть ортогональными, если их скалярное произведение равно нулю:
будем называть ортогональными, если их скалярное произведение равно нулю:

Равенство (12.5) является аналогом условия перпендикулярности векторов в двух- и трехмерном случаях, когда в равенстве (12.4) cosφ = 0.
Линейная зависимость векторов
