Глава 6. неопределенный интеграл

Первообразная и неопределенный интеграл

Понятие первообразной функции

Предыдущие главы были посвящены одной из основных за­дач дифференциального исчисления — нахождению производ­ной заданной функции. Множество вопросов математическо­го анализа и приложений в разнообразных науках приводит к другой задаче: по данной функции f(x) найти такую функцию F(x), производная которой равна функции f(x).

Определение 1. Функция F(x) называется первообразной для функции f(x) на промежутке X, если для любого х 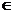Х функ­ция F(x) дифференцируема и выполняется равенство F'(x) = f(x).

Приведем примеры.

Пример 1. Функция F(x) = sin x является первообразной для функции f(x) = cos x на бесконечном промежутке (- , + ), так как при любых х выполнено равенство (sin x)' = cos х.

Пример 2. Функция F(x) = ln x — первообразная для функ­ции f(x) = 1/x на промежутке (0, + ), так как в каждой точке этого интервала выполнено равенство (ln x)' =1/x.

Заметим, что задача отыскания по заданной функции f(x) еe первообразной неоднозначна; если F(x) — первообразная, то и функции F(x) + С, где С - произвольное постоянное число, также первообразная для функции f(x), так как [F(x) + С]' = f(x).

Неопределенный интеграл

Определение 2. Совокупность всех первообразных функций для функции f(x) на промежутке Х называется неопределен­ным интегралом от функции f(x) на этом промежутке и обо­значается символом

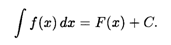
В этом обозначении 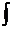называется знаком интеграла (это стилизованная латинская буква S, означающая суммирование), f(x) — подынтегральной функцией, f(x)dx — подынтеграль­ным выражением, а переменная х — переменной интегриро­вания.

Операция нахождения первообразной по ее производной или неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции. Интег­рирование является операцией, обратной дифференцированию. Для проверки правильности выполнения интегрирования нуж­но продифференцировать результат и получить при этом подынтегральную функцию.

Рассмотрим примеры.

Пример 3. 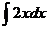= x² + С; проверка: (x² + С)' = 2х.

Пример 4. 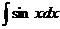= - cos х + С; проверка: (-cos х + С)' = sin x.

Пример 5. 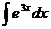= 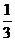е^3x + С; проверка: ( 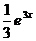+ C)' = е^3x.

Основные свойства неопределенного интеграла

Прежде всего укажем свойства, которые непосредственно вытекают из определения неопределенного интеграла.

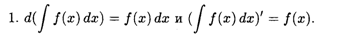
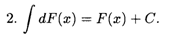
Следующие два свойства называются линейными свойст­вами неопределенного интеграла.

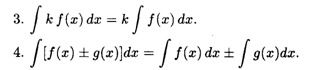
Заметим, что последнее свойство справедливо для любого конечного числа слагаемых в подынтегральной функции.

Таблица основных неопределенных интегралов

Ранее мы получили таблицу основных производных эле­ментарных функций. Приводимая ниже таблица основных не­определенных интегралов представляет собой вычислитель­ный аппарат интегрального исчисления. Часть формул таб­лицы непосредственно следует из определения интегрирования как операции, обратной дифференцированию. Справедливость всех формул легко проверить дифференцированием.

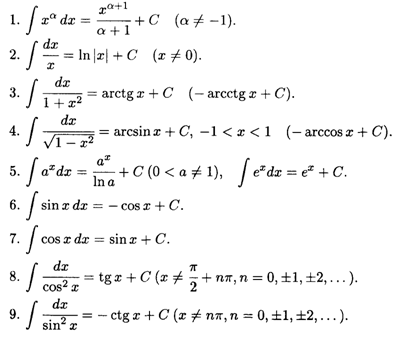
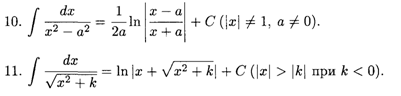
Интегралы этой таблицы принято называть табличными.

Как было установлено в п. 4.4, операция дифференцирова­ния не выводит нас из класса элементарных функций. С опе­рацией интегрирования дело обстоит иначе: интегралы от не­которых элементарных функций уже не являются элементар­ными функциями. Укажем некоторые из них.

Каждый из этих интегралов есть функция, которая не яв­ляется элементарной, хотя подынтегральные функции в этих интегралах являются элементарными. Они играют большую роль в прикладных науках; так, интеграл 1 является одним из основных в теории вероятностей и статистике.

Как правило, интегралы, с которыми приходится иметь де­ло в различных приложениях, не выражаются элементарными функциями (или, как принято говорить, являются "неберущи­мися"). Тем не менее существуют достаточно хорошо разрабо­танный аппарат приближенных формул с использованием эле­ментарных функций и методы приближенных расчетов, поз­воляющие с любой степенью точности оценивать и вычислять "неберущиеся" интегралы.