Системы линейных уравнений и матрицы
Кафедра высшей математики
И.В. Трофимова
Математика
Рабочая программа, методические указания и контрольные задания для студентов I курса заочной формы обучения специальностей 140401 (070200), 220301 (210200), 260601 (170600), 260602 (271300)
Часть 1

www.mgutm.ru
Москва – 2010
УДК 51
Ó И.В. Трофимова. Математика. Рабочая программа, методические указания и контрольные задания для студентов заочной формы обучения I курса специальностей 140401 (070200), 220301 (210200), 260601 (170600), 260602 (271300). Часть 1. – М.: МГУТУ, 2010.
Рекомендовано Институтом информатизации образования РАО,
сертификат № _______
Методические указания и контрольные задания по различным разделам высшей математики разработаны в соответствии с программой курса «Математика» и предназначены для студентов заочной формы обучения специальностей 140401 (070200), 220301 (210200), 260601 (170600), 260602 (271300).
Цель издания – оказание методической помощи студентам при самостоятельном изучении дисциплины и выполнении контрольных заданий.
Автор: Трофимова И.В.
Рецензент: к.п.н., доцент Садыкова А.Р.
ÓМосковский государственный университет технологий и управления, 2010
109004, Москва, Земляной вал, 73
Содержание
Тематическое содержание рабочей программы по дисциплине «Математика» для специальностей 2102, 0702................................................................................. 4
Тематическое содержание рабочей программы по дисциплине «Математика» для специальностей 1706, 2713................................................................................. 8
Указания по выполнению контрольных работ................................................ 11
Контрольная работа № 1.................................................................................. 12
Указания к решению задач контрольной работы № 1.................................... 15
Контрольная работа № 2.................................................................................. 24
Указания к решению задач контрольной работы № 2.................................... 28
Контрольная работа № 3.................................................................................. 34
Указания к решению задач контрольной работы № 3.................................... 38
Контрольная работа № 4.................................................................................. 45
Указания к решению задач контрольной работы № 4.................................... 50
Приложения....................................................................................................... 54
Список литературы........................................................................................... 56
Тематическое содержание рабочей программы по дисциплине «Математика» для специальностей 2102, 0702
Алгебра и геометрия
Системы линейных уравнений и матрицы
Определители и алгебра матриц: определение, свойства, сложение и умножение матриц, умножение матрицы на число, транспонирование матриц. Обратная матрица. Ранг матрицы. Группы невырожденных квадратных матриц по умножению.
Системы линейных алгебраических уравнений. Формулы Крамера, метод Гаусса. Общая теория систем линейных уравнений (критерий совместности, общее решение и фундаментальная система решений).
Векторная алгебра
Векторы и линейные операции над ними. Коллинеарность и компланарность векторов. Линейная зависимость систем векторов. Описание базисов плоскости и пространства. Координаты векторов в базисе плоскости и пространства. Действия над векторами, заданными своими координатами. Критерии коллинеарности и компланарности векторов в координатах. Скалярное, векторное и смешанное произведения векторов, их свойства и геометрический смысл.
Алгебраические структуры
Отношения. Бинарные отношения на множествах. Алгебраические структуры: группа, кольцо, поле. Алгебры. Алгебраические системы. Булева алгебра.
Кольцо целых чисел. Теория делимости в кольце целых чисел. Кольца классов вычетов.
Поле комплексных чисел.
Кольцо многочленов от одной переменной, теория делимости. Многочлены от нескольких переменных.
Дискретная математика
Комбинаторика
Предмет комбинаторики. Правило суммы и правило произведения. Принцип включения и исключения. Размещения, перестановки, сочетания без повторений и с повторениями.
Биноминальные коэффициенты и соотношения для них. Задачи перечисления.
Математическая логика
Основные понятия логики: высказывания и рассуждения. Основные логические связки. Алгебра высказываний. Логические функции и способы их задания – таблицы и формулы. Функциональная полнота. Булева алгебра и ее законы.
Дизъюнктивные и конъюнктивные нормальные формы.
Логика предикатов. Предметная область и предметные переменные. Кванторы общности и существования. Свободные и связанные переменные. Эквивалентные соотношения в логике предикатов. Общезначимые и противоречивые формулы. Запись утверждений естественного языка в логике предикатов.
Теория графов
Неориентированные и ориентированные графы, мультиграфы и кратные ребра. Смежность и инцидентность. Способы представления графов. Матрица смежности. Графы и бинарные отношения. Изоморфизм графов. Полные графы и клики. Двудольные графы.
Пути, циклы, цепи, простые цепи в неориентированных графах. Связность и компоненты связности. Расстояния. Центр, радиус, диаметр графа. Обходы графов.
Виды связности в ориентированных графах.
Матрицы графов и операции над ними.
Деревья и их свойства. Корневые деревья. Приложения деревьев: иерархии, классификации. Обходы деревьев.
Теория алгоритмов
Алгоритм Евклида и оптимизационные задачи на графах. Минимальное остовное дерево. Кратчайшие пути и алгоритм Дейкстры. Потоки в сетях: определения, понятие увеличивающей цепи, алгоритм нахождения минимального потока. Понятие о сложности, переборных и трудно вычислимых задачах.
Математический анализ
Введение в анализ
Функции. Последовательности. Предел последовательности и предел функции. Бесконечно малые и бесконечно большие величины. Замечательные пределы. Эквивалентные бесконечно малые функции. Непрерывность функций, точки разрыва.
Неопределенный интеграл
Неопределенный интеграл и его свойства. Таблица неопределенных интегралов. Методы интегрирования: непосредственное интегрирование, метод подстановки, интегрирование по частям. Интегрирование основных классов элементарных функций.
Определенный интеграл
Определенный интеграл и его свойства. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. Метод интегрирования подстановкой. Интегрирование по частям. Геометрические приложения определенного интеграла: вычисление площадей плоских фигур, длины дуги плоской кривой, объема тела, площади поверхности вращения и др. физические приложения определенного интеграла: вычисление работы, давления и др.
Несобственные интегралы I и II рода, признаки их сходимости.
Тематическое содержание рабочей программы по дисциплине «Математика» для специальностей 1706, 2713
Алгебра и геометрия
Векторная алгебра
Векторы и линейные операции над ними. Коллинеарность и компланарность векторов. Линейная зависимость систем векторов. Описание базисов плоскости и пространства. Координаты векторов в базисе плоскости и пространства. Действия над векторами, заданными своими координатами. Критерии коллинеарности и компланарности векторов в координатах. Скалярное, векторное и смешанное произведения векторов, их свойства и геометрический смысл.
Математический анализ
Введение в анализ
Функции. Последовательности. Предел последовательности и предел функции. Бесконечно малые и бесконечно большие величины. Замечательные пределы. Эквивалентные бесконечно малые функции. Непрерывность функций, точки разрыва.
Неопределенный интеграл
Неопределенный интеграл и его свойства. Таблица неопределенных интегралов. Методы интегрирования: непосредственное интегрирование, метод подстановки, интегрирование по частям. Интегрирование основных классов элементарных функций.
Определенный интеграл
Определенный интеграл и его свойства. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. Метод интегрирования подстановкой. Интегрирование по частям. Геометрические приложения определенного интеграла: вычисление площадей плоских фигур, длины дуги плоской кривой, объема тела, площади поверхности вращения и др. физические приложения определенного интеграла: вычисление работы, давления и др. Несобственные интегралы I и II рода, признаки их сходимости.
Контрольная работа №1
Задача 1.1.Решить систему уравнений: а) методом Гаусса; б) по формулам Крамера; в) с помощью обратной матрицы.
1. 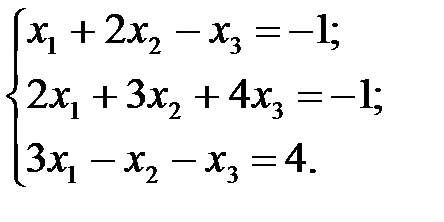 2.
2. 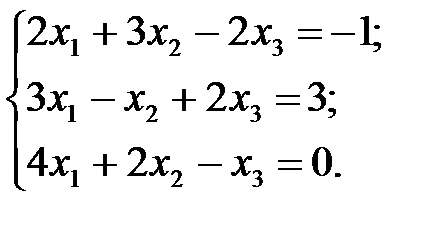
3. 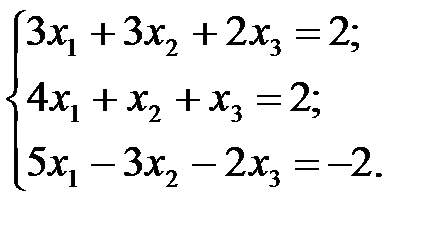 4.
4. 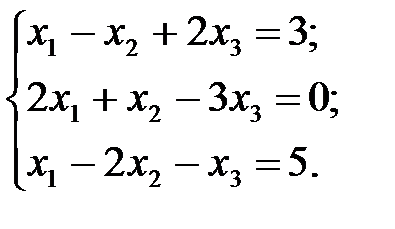
5. 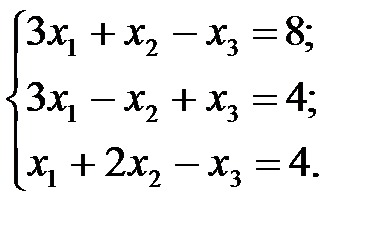 6.
6. 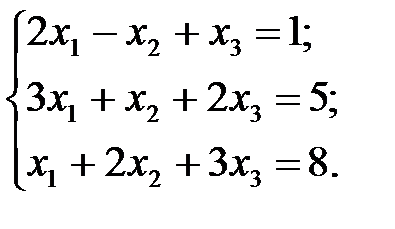
7. 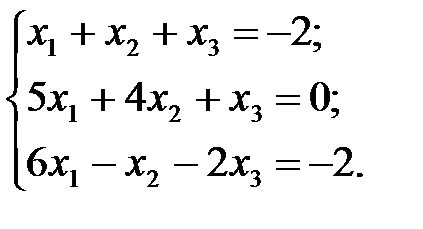 8.
8. 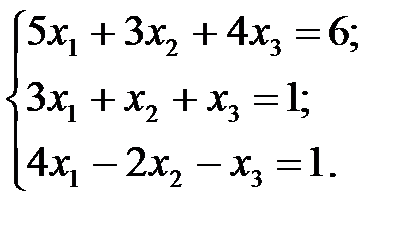
9. 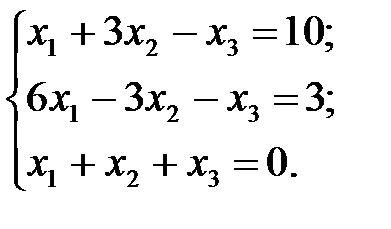 10.
10. 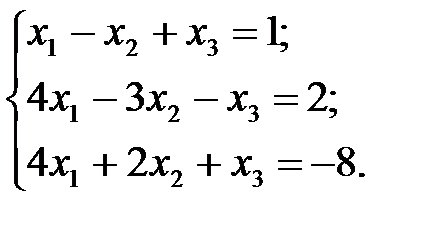
Задача 1.2.Исследовать, имеет ли нетривиальные решения однородная система уравнений. В случае положительного ответа, найти ее общее решение. Записать фундаментальную систему решений.
1. 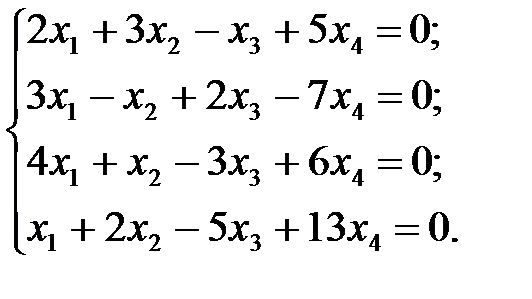 2.
2. 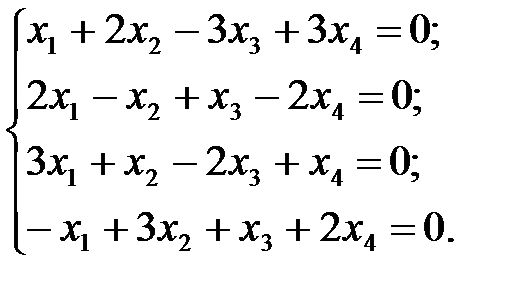
3. 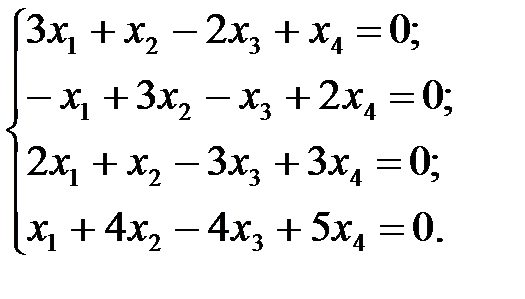 4.
4. 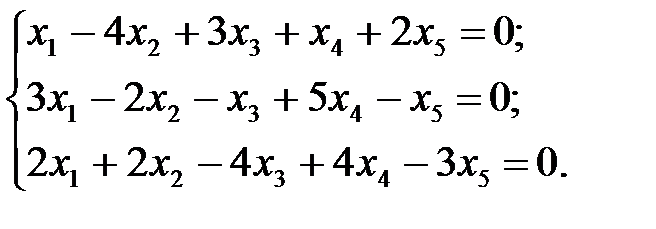
5. 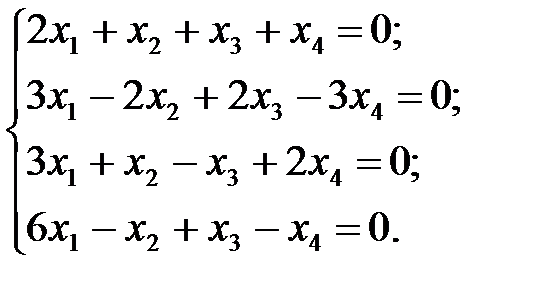 6.
6. 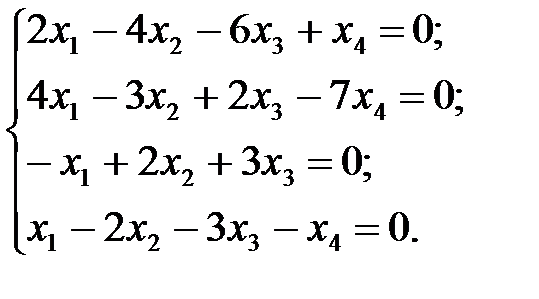
7. 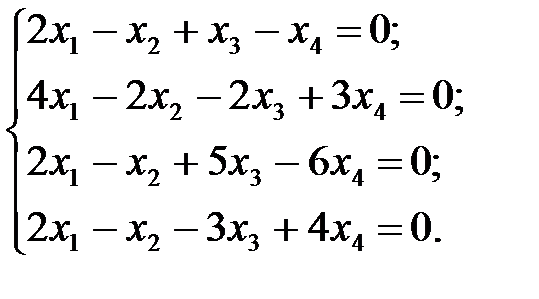 8.
8. 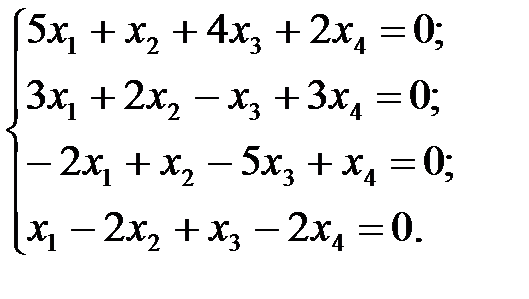
9. 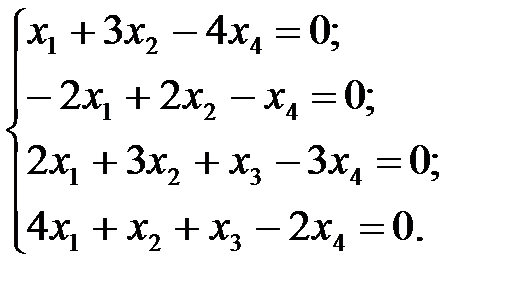 10.
10. 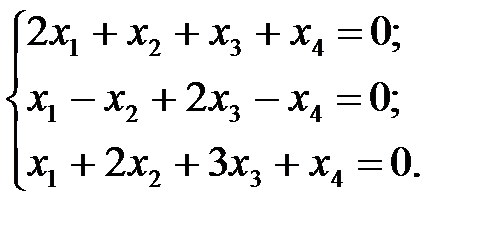
Задача 1.3.Даны координаты векторов 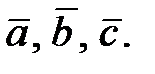 Найти:
Найти:
1) длину вектора 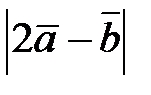 ;
;
2) скалярное произведение векторов 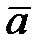 и
и 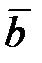 ;
;
3) косинус угла между векторами 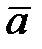 и
и 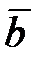 ;
;
4) векторное произведение векторов 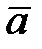 и
и 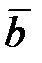 ;
;
5) площадь параллелограмма 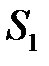 и площадь треугольника
и площадь треугольника 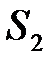 , построенных на векторах
, построенных на векторах 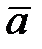 и
и 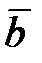 ;
;
6) смешанное произведение векторов 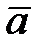 ,
, 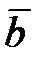 и
и 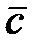 ;
;
7) объем параллелепипеда 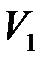 и объем пирамиды
и объем пирамиды 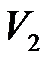 , построенных на векторах
, построенных на векторах 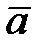 ,
, 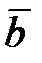 и
и 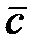 .
.
1. 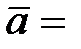 (2; 3; 1),
(2; 3; 1), 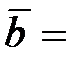 (2; 3; 4),
(2; 3; 4), 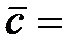 (3; 1; –1).
(3; 1; –1).
2. 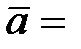 (1; –1; –3),
(1; –1; –3), 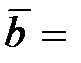 (2; 3; 1),
(2; 3; 1), 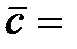 (2; 3; 4).
(2; 3; 4).
3. 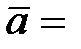 (3; 1; –1),
(3; 1; –1), 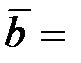 (–2; –1; 0),
(–2; –1; 0), 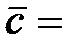 (5; 2; –1).
(5; 2; –1).
4. 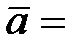 (4; 3; 1),
(4; 3; 1), 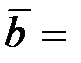 (6; 7; 4),
(6; 7; 4), 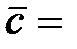 (2; 0; –1).
(2; 0; –1).
5. 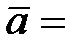 (–3; 3; 1),
(–3; 3; 1), 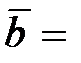 (1; 0; –3),
(1; 0; –3), 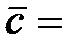 (2; 1; 6).
(2; 1; 6).
6. 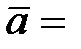 (1; –2; 6),
(1; –2; 6), 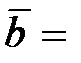 (1; 0; 1),
(1; 0; 1), 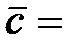 (2; –6; 7).
(2; –6; 7).
7. 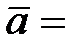 (1; 3; 7),
(1; 3; 7), 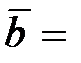 (-1; 3; 5),
(-1; 3; 5), 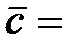 (-6; 0; 2).
(-6; 0; 2).
8. 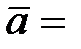 (4; 0; 3),
(4; 0; 3), 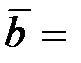 (1; –2; 4),
(1; –2; 4), 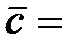 (1; –1; 2).
(1; –1; 2).
9. 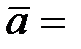 (2; 3; 2),
(2; 3; 2), 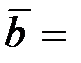 (4; 6; 3),
(4; 6; 3), 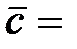 (2; –1; 3).
(2; –1; 3).
10. 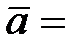 (3; 10; 5),
(3; 10; 5), 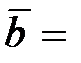 (–2; –2; –3),
(–2; –2; –3), 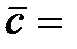 (2; 4; 3).
(2; 4; 3).
Задача 1.4.Известны координаты вершин треугольника ABC. Необходимо:
1) найти координаты вектора, перпендикулярного прямой BC и угловой коэффициент k этой прямой;
2) составить уравнение прямой AA1, параллельной прямой BC;
3) составить уравнение высоты AH;
4) составить уравнение медианы BM;
5) найти координаты точки пересечения E прямых AH и BM;
6) найти длину высоты AH.
| 1. | A (2; –2), | B (5; 4), | C (–2; 0). |
| 2. | A (–2; 2), | B (–5; –4), | C (2; 0). |
| 3. | A (–2; –2), | B (–5; 4), | C (2; 0). |
| 4. | A (2; 2), | B (5; –4), | C (–2; 0). |
| 5. | A (2; –2), | B (–4; –5), | C (0; 2). |
| 6. | A (2; 2), | B (–4; 5), | C (0; –2). |
| 7. | A (–2; –2), | B (4; –5), | C (0; 2). |
| 8. | A (1; –2), | B (4; 4), | C (–3; 0). |
| 9. | A (–1; 2), | B (–4; –4), | C (3; 0). |
| 10. | A (–1; –2), | B (–4; 4), | C (3; 0). |
Задача 1.5.Выяснить, какие кривые определяются следующими уравнениями. Построить графики кривых.
1. а) 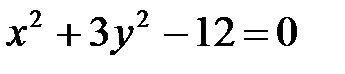 ; б)
; б) 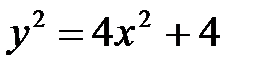 ; в)
; в) 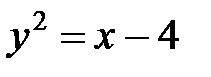 .
.
2. а) 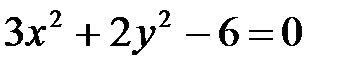 ; б)
; б) 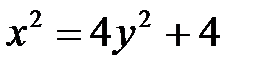 ; в)
; в) 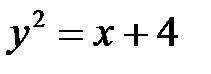 .
.
3. а) 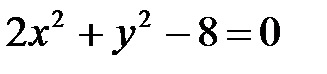 ; б)
; б) 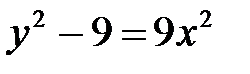 ; в)
; в) 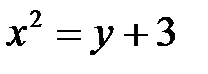 .
.
4. а) 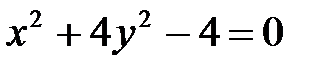 ; б)
; б) 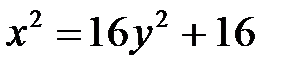 ; в)
; в) 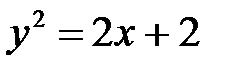 .
.
5. а) 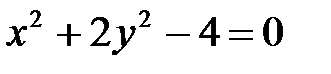 ; б)
; б) 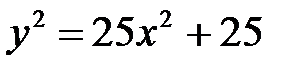 ; в)
; в) 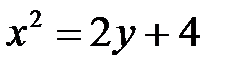 .
.
6. а) 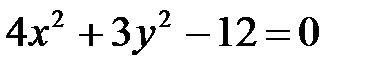 ; б)
; б) 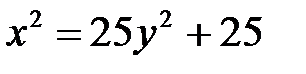 ; в)
; в) 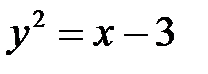 .
.
7. а) 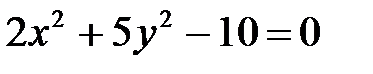 ; б)
; б) 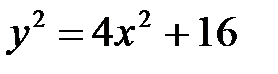 ; в)
; в) 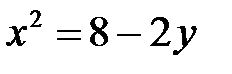 .
.
8. а) 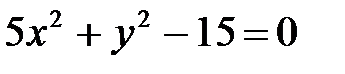 ; б)
; б) 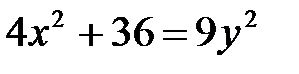 ; в)
; в) 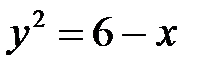 .
.
9. а) 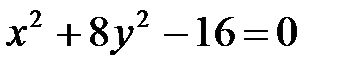 ; б)
; б) 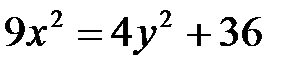 ; в)
; в) 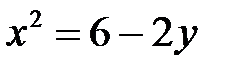 .
.
10. а) 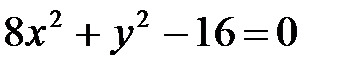 ; б)
; б) 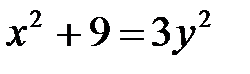 ; в)
; в) 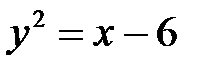 .
.
Задача 1.6. Известны координаты точек A, B, C и D. Необходимо:
1) составить уравнение плоскости ABC;
2) вычислить угол между плоскостями ABC и xOy;
3) вычислить угол между плоскостью ABC и осью Oz;
4) составить уравнение плоскости P, проходящей через точки B и C, перпендикулярно плоскости xOy;
5) составить канонические уравнения перпендикуляра AF к плоскости P;
6) вычислить координаты точки F;
7) найти длину перпендикуляра AF.
| 1. | A (0; −2; 0), | B (3; 2; −2), | C (−3; 6; 2), | D (0; 4; 6). |
| 2. | A (−1; −1; 0), | B (2; 3; -2), | C (−4; 7; 2), | D (−1; 5; 6). |
| 3. | A (1; −3; 0), | B (4; 1; -2), | C (−2; 5; 2), | D (1; 3; 6). |
| 4. | A (1; −2; -1), | B (4; 2; −3), | C (−2; 6; 1), | D (1; 4; 5). |
| 5. | A (0; −3; 1), | B (3; 1; −1), | C (−3; 5; 3), | D (0; 3; 7). |
| 6. | A (1; −1; 0), | B (4; 3; -2), | C (−2; 7; 2), | D (1; 5; 6). |
| 7. | A (0; −1; 1), | B (3; 3; −1), | C (−3; 7; 3), | D (0; 5; 7). |
| 8. | A (−1;−2; −1), | B (2; 2; −3), | C (−4; 6; 1), | D (−1; 4; 5). |
| 9. | A (1; −2; 1), | B (4; 2; −1), | C (−2; 6; 3), | D (1; 4; 7). |
| 10. | A (0; −1; −1), | B (3; 3; −3), | C (−3; 7; 1), | D (0; 5; 5). |
К задаче 1.1
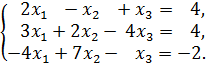
а) Решим систему методом Гаусса. Запишем расширенную матрицу системы и приведем ее к треугольному виду при помощи элементарных преобразований матрицы, выполненных над строками:
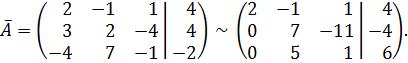
Здесь оставили первую строку без изменения, затем первую строку умножили на (−3), а вторую на 2, сложили их и записали второй строкой, после чего первую строку умножили на 2, сложили с третьей строкой и записали третьей строкой.
Затем, оставив первую и вторую строки без изменений, умножим вторую строку на (−5), а третью – на 7, сложим их и запишем третьей строкой:
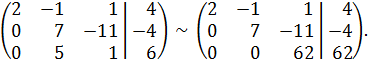
Ранг основной матрицы равен рангу расширенной матрицы и равен количеству неизвестных
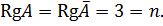
Система совместна, имеет единственное решение.
Поставим в соответствие расширенной матрице систему, эквивалентную исходной, решение которой совершаем снизу вверх:
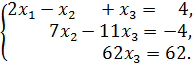
Из третьего уравнения получим 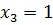 . Подставляя значение
. Подставляя значение 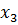 во второе уравнение, получим
во второе уравнение, получим 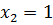 . Подставляя значения
. Подставляя значения 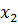 и
и 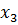 в первое уравнение, получим
в первое уравнение, получим 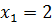 .
.
Ответ: (2; 1; 1).
б) Решим систему уравнений по формулам Крамера. Формулы Крамера имеют вид:
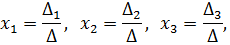
где  – определитель системы,
– определитель системы, 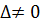 ;
; 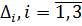 получим из определителя
получим из определителя  системы, заменой i-го столбца столбцом свободных членов.
системы, заменой i-го столбца столбцом свободных членов.
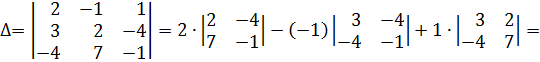
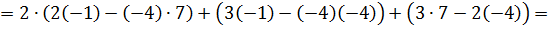
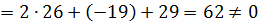 .
.
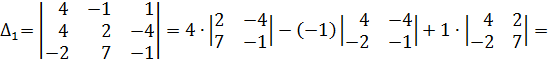 124,
124,
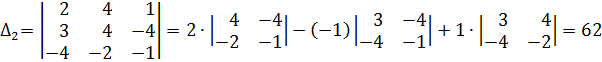 ,
,
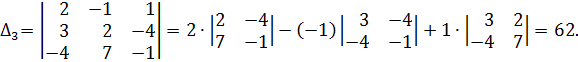
Значит, по формулам Крамера
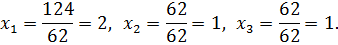
в) Решим систему с помощью обратной матрицы. Запишем систему в матричной форме
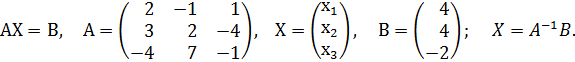
Найдем обратную матрицу 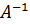 . Определитель системы
. Определитель системы 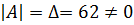 , значит, матрица
, значит, матрица 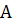 невырожденная и имеет обратную матрицу, определяемую по формуле
невырожденная и имеет обратную матрицу, определяемую по формуле
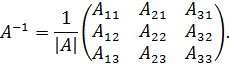
Вычислим алгебраические дополнения элементов матрицы:
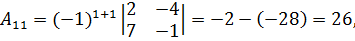
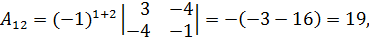
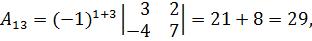
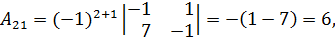
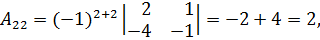
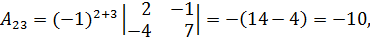
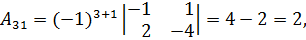
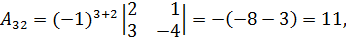
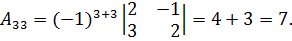
Таким образом,
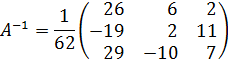
и искомое решение имеет вид
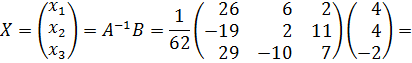
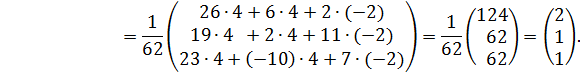
К задаче 1.2
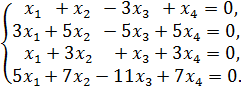
Выпишем матрицу системы и выполним элементарные преобразования строк матрицы. Для этого поочередно первую строку умножим на (–3), (–1) и
(–5) и сложим соответственно со второй, третьей и четвертой строками. Затем умножим вторую строку преобразованной матрицы на (–1) и сложим ее с третьей и четвертой строками. В результате получим матрицу с двумя нулевыми строками.
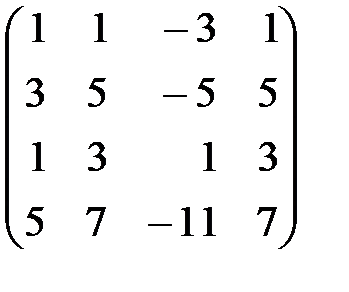 ~
~ 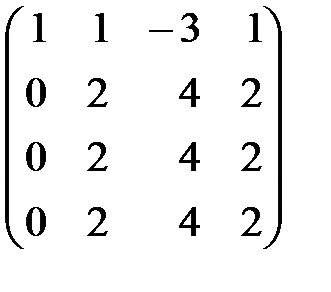 ~
~ 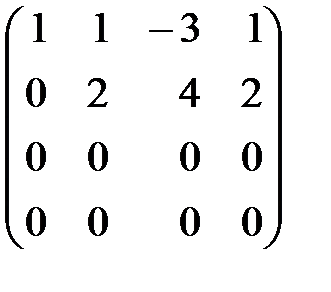 ~
~ 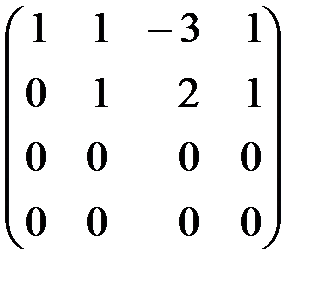 .
.
Ранг матрицы A равен 2 и меньше количества неизвестных 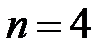 . Следовательно, система имеет нетривиальное решение.
. Следовательно, система имеет нетривиальное решение.
Базисный минор – 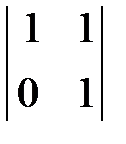 , базисные переменные –
, базисные переменные – 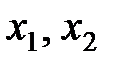 ; свободные переменные –
; свободные переменные – 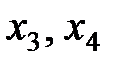 . Сокращенная система имеет вид
. Сокращенная система имеет вид
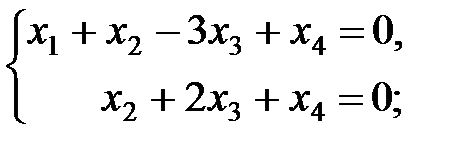 Û
Û 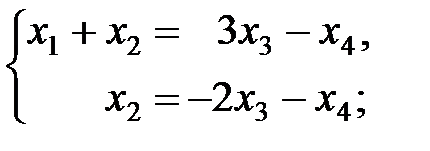 Û
Û 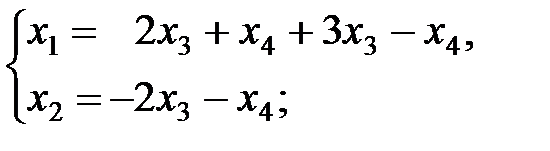 Û
Û
Û 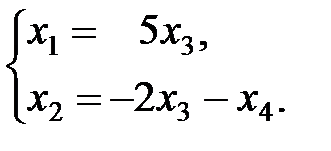
Пусть 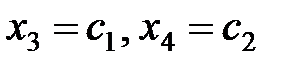 . Получим общее решение в виде:
. Получим общее решение в виде:
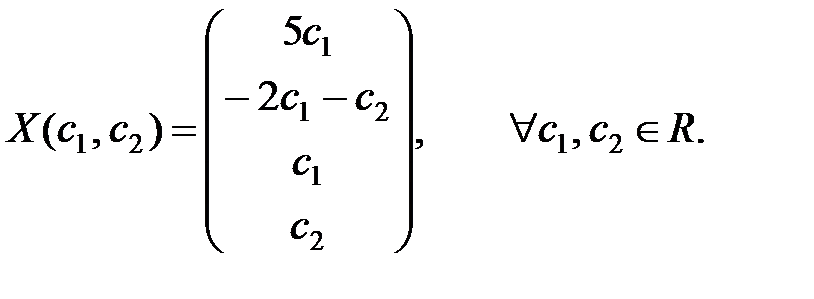
Положив 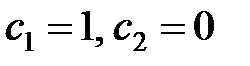 и
и 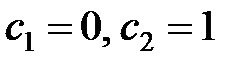 , из общего решения получим фундаментальную систему решений:
, из общего решения получим фундаментальную систему решений:
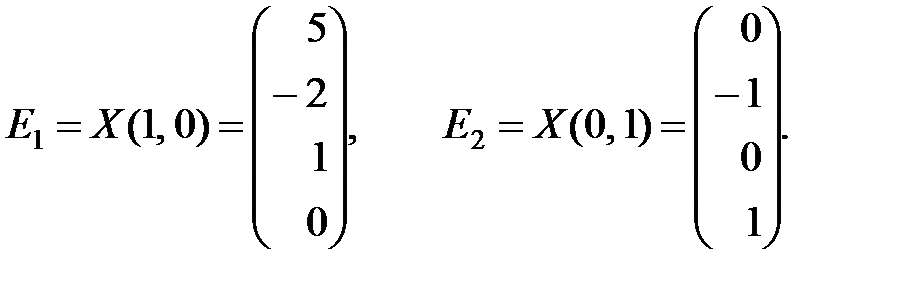
К задаче 1.3
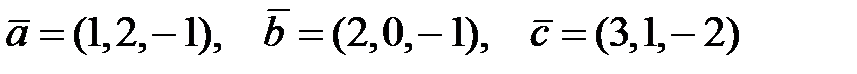 .
.
1) Определим координаты вектора 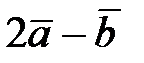 :
:
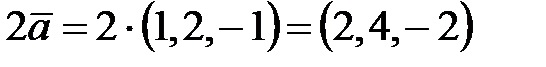 ;
;
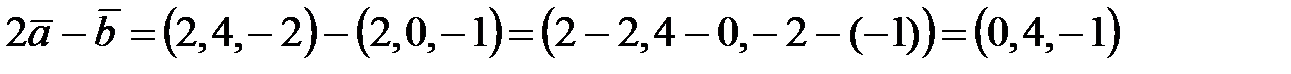 .
.
Определим длину вектора 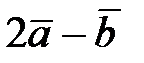 :
:
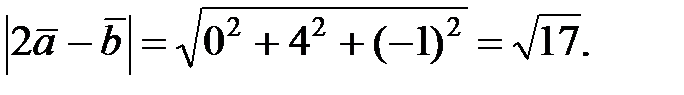
2) Найдем скалярное произведение векторов 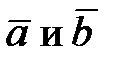 :
:
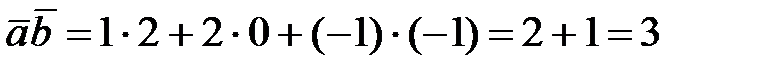 .
.
3) Косинус угла 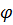 между векторами
между векторами 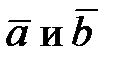 найдем по формуле
найдем по формуле

Длины векторов 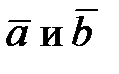 равны
равны
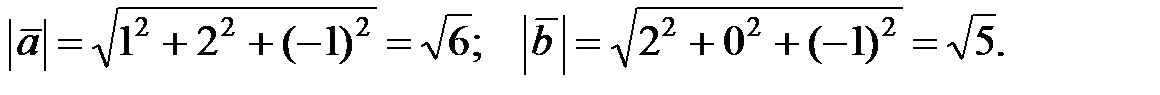 Значит, по формуле (1)
Значит, по формуле (1)
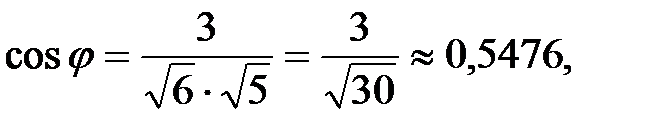
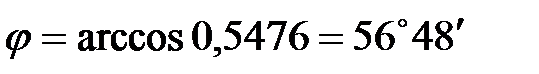 .
.
4) Имеем
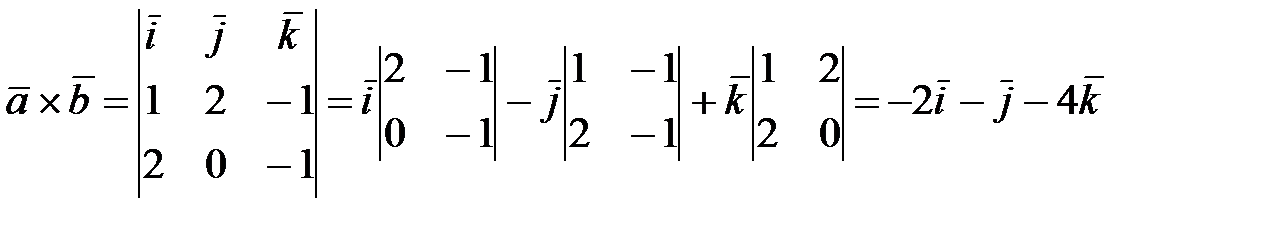 .
.
5) Площадь 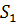 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 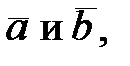
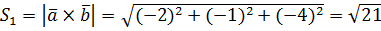 (кв. ед.).
(кв. ед.).
Площадь 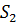 треугольника, построенного на векторах
треугольника, построенного на векторах 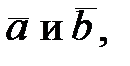
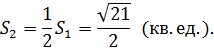
6) Объем 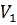 параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах 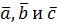 , равен
, равен
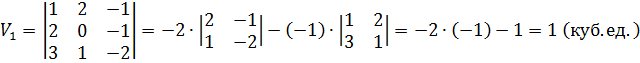
Объем 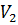 пирамиды, построенной на векторах
пирамиды, построенной на векторах 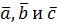 , равен
, равен
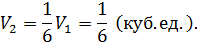
К задаче 1.4
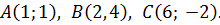
1) Запишем уравнение прямой BC как уравнение прямой, проходящей через две точки, по формуле:
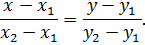
Имеем
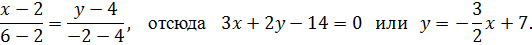
Координаты нормального вектора, перпендикулярного прямой BC 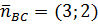 , угловой коэффициент
, угловой коэффициент 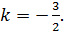
2) Составим уравнение прямой 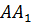 , параллельной прямой
, параллельной прямой 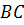 . Так как прямые
. Так как прямые 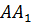 и
и 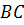 параллельны, то их угловые коэффициенты равны
параллельны, то их угловые коэффициенты равны
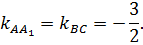
Составим уравнение прямой 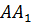 по формуле
по формуле
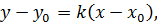
где 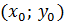 координаты точки A,
координаты точки A, 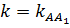 . Имеем
. Имеем
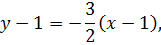
отсюда 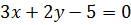 – уравнение прямой, параллельной прямой BC.
– уравнение прямой, параллельной прямой BC.
3) Составим уравнение высоты AH. Так как прямая AH перпендикулярна прямой BC, то
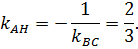
Находим уравнение высоты:
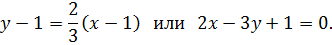
4) Составим уравнение медианы BM. Найдем координаты точки M – середины отрезка AC:
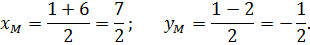
Запишем уравнение прямой BM как уравнение прямой, проходящей через две точки B и M:
ng w:val="RU"/></w:rPr><m:t>,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 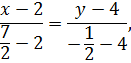
отсюда 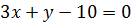 – уравнение медианы BM.
– уравнение медианы BM.
5) Найдем координаты точки E пересечения прямых AH и BM, решив систему уравнений:
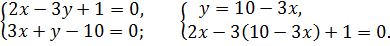
Отсюда 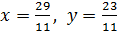 . Точка
. Точка 
6) Найдем длину высоты AH как расстояние от точки A до прямой BC по формуле

где 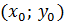 – координаты точки A,
– координаты точки A, 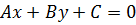 – общее уравнение прямой BC.
– общее уравнение прямой BC.
Получим по формуле (2)
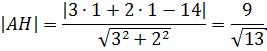
К задаче 1.5
а) 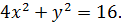
Уравнение кривой получим, разделив обе части данного уравнения на 16:
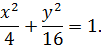
Получили эллипс, полуоси которого 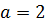 и
и 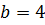 .
.
Построим эллипс (рис. 1).
| x |
| y |
| −2 |
| −4 |
| Рис. 1 |
б) 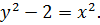
Уравнение кривой получим, разделив обе части данного уравнения на 2:
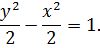
Получили гиперболу с одинаковыми полуосями 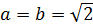 . Фокусы гиперболы находятся на оси
. Фокусы гиперболы находятся на оси 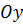 . Уравнения асимптот
. Уравнения асимптот 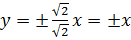 .
.
Строим гиперболу, причем сначала построим ее асимптоты (рис. 2).
| x |
| y |
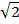 |
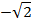 |
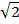 |
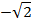 |
| Рис. 2 |
в) > 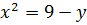 .
.
Уравнение кривой получим, преобразовав уравнение к виду
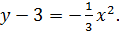 Точка
Точка 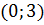 – вершина параболы. Ветви параболы направлены вниз. Парабола симметрична относительно оси
– вершина параболы. Ветви параболы направлены вниз. Парабола симметрична относительно оси 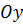 .
.
Строим параболу (рис. 3).
| x |
| y |
| −3 |
| Рис. 3 |
К задаче 1.6
| A (2; 1; −1), | B (3; 0; 2), | C (−1; 2; 2), | D (0; 1; −3). |
1) Пусть 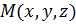 – произвольная точка плоскости. Тогда векторы
– произвольная точка плоскости. Тогда векторы 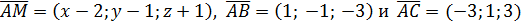 компланарны, поэтому
компланарны, поэтому
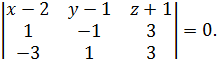
Раскрывая определитель, получим 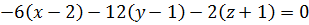
или 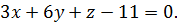 Это и есть искомое уравнение плоскости.
Это и есть искомое уравнение плоскости.
2) Выпишем координаты перпендикулярных к плоскостям ABC и xOy векторов 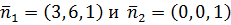 . Тогда, по формуле (1),
. Тогда, по формуле (1),
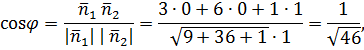
то есть 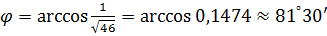 .
.
3) В качестве направляющего вектора оси Oz можно взять вектор
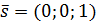 . Так как нормальный вектор
. Так как нормальный вектор 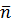 плоскости ABC имеет координаты
плоскости ABC имеет координаты 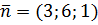 , то
, то
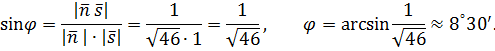
4) Вектор 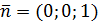 , перпендикулярный данной плоскости xOy
, перпендикулярный данной плоскости xOy
(или 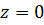 ), будет, очевидно, параллелен искомой. Таким образом, искомая плоскость проходит через точки B и C параллельно вектору
), будет, очевидно, параллелен искомой. Таким образом, искомая плоскость проходит через точки B и C параллельно вектору 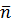 .
.
Пусть 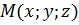 – произвольная точка искомой плоскости, тогда векторы
– произвольная точка искомой плоскости, тогда векторы 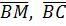 и
и 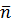 компланарны, следовательно, их смешанное произведение равно нулю:
компланарны, следовательно, их смешанное произведение равно нулю:
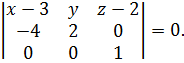
Вычисляя определитель, получим искомое уравнение плоскости
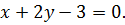
5) Вектор 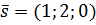 , перпендикулярный плоскости P, будет направляющим вектором перпендикуляра AF. Поэтому канонические уравнения этого перпендикуляра имеют вид
, перпендикулярный плоскости P, будет направляющим вектором перпендикуляра AF. Поэтому канонические уравнения этого перпендикуляра имеют вид
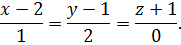
6) Параметрические уравнения прямой AF:
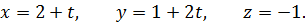
Подставляя значения 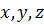 в уравнение плоскости P
в уравнение плоскости P
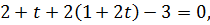
найдем значение параметра 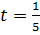 , отвечающее точке F как точке пересечения прямой AF с плоскостью P. Следовательно,
, отвечающее точке F как точке пересечения прямой AF с плоскостью P. Следовательно,
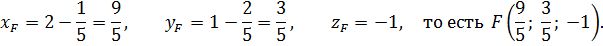
7) Найдем длину AF: 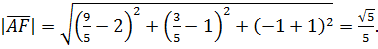
Контрольная работа №2
Задача 2.1.Даны комплексные числа 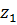 и
и 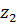 . Вычислить
. Вычислить 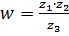 , где
, где
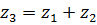 . Для контроля проверить равенство
. Для контроля проверить равенство 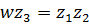 .
.
1. 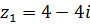 ,
, 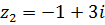 .
.
2. 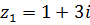 ,
, 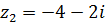 .
.
3. 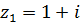 ,
, 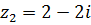 .
.
4. 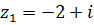 ,
, 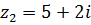 .
.
5. 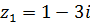 ,
, 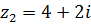 .
.
6. 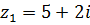 ,
, 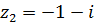 .
.
7. 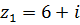 ,
, 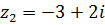 .
.
8. 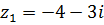 ,
, 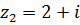 .
.
9. 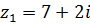 ,
, 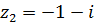 .
.
10. 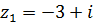 ,
, 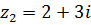 .
.
Задача 2.2.Решить уравнение:
1. 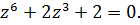 2.
2. 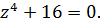
3. 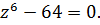 4.
4. 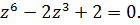
5. 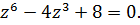 6.
6. 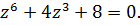
7. 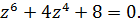 8.
8. 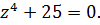
9. 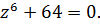 10.
10. 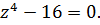
Задача 2.3.
1. Автобусу, в котором находится 10 пассажиров, предстоит сделать 5 остановок. Сколькими способами могут распределиться пассажиры между этими остановками, начиная со второй?
2. Общество из 20 членов выбирает открытым голосованием из своего состава одного представителя. Сколькими способами может произойти голосование, если каждый голосует за одного человека (быть может, и за себя)?
3. Общество из 20 человек выбирает «тайным» голосованием (учитывается лишь число голосов, полученных каждым кандидатом, но неизвестно, кто за него голосовал) из своего состава одного представителя. Сколькими способами может произойти голосование, если каждый голосует за одного человека?
4. Сколькими способами можно разделить на команды по 5 человек для игры в баскетбол группу из 20 человек?
5. Сколькими способами 3 человека могут разделить между собой 2 яблока, 5 груш, 4 сливы, 3 апельсина и 1 мандарин (фрукты одного вида считаются одинаковыми)?
6. Переплетчик должен переплести 12 одинаковых книг в красный, зеленый и синий переплеты. Сколькими способами он может это сделать?
7. Сколькими способами можно разделить на команды по 6 человек для игры в волейбол группу из 24 человек?
8. Сколькими способами 4 черных шара, 6 белых шаров и 2 красных шара можно разложить в 6 различных ящиков?
9. Ско
