Комбинаторика. бином ньютона

Перестановки. Факториал. Размещения. Сочетания.

Бином Ньютона. Биномиальные коэффициенты.

Треугольник Паскаля. Свойства биномиальных коэффициентов.

Общим термином «соединения» мы будем называть три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.).

Перестановки. Возьмём n различных элементов: a₁ , a₂ , a₃ , …, a_n . Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается P_n . Это число равно произведению всех целых чисел от 1 до n :

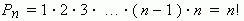
Символ n! ( называется факториал ) - сокращённая запись произведения: 1 · 2 · 3 · … · ( n – 1 ) · n .

П р и м е р . Найти число перестановок из трёх элементов: a, b, c.

Р е ш е н и е . В соответствии с приведенной формулой: P₃ = 1 · 2 · 3 = 6.
Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.

Размещения. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m .

Их общее количество обозначается: 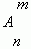и равно произведению:

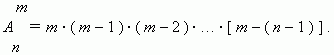
П р и м е р . Найти число размещений из четырёх элементов a, b, c, d по два.

Р е ш е н и е . В соответствии с формулой получим:

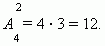
Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

Сочетания. Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, не принимая во внимание порядок расположения этих m элементов. Тогда мы получим сочетания из n элементов по m .

Их общее количество обозначается 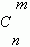и может быть вычислено по формуле:

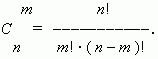
Из этой формулы ясно, что

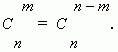
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1,что является определением 0! .

В соответствии с этим определением получим:

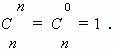
Общее число сочетаний можно вычислить, пользуясь и другим выражением:

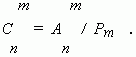
П р и м е р . Найти число сочетаний из пяти элементов: a, b, c, d, e по три.

Р е ш е н и е :

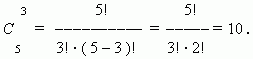
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Бином Ньютона. Это формула, представляющая выражение ( a + b ) ⁿ при положительном целом n в виде многочлена:

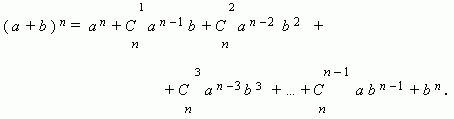
Заметим, что сумма показателей степеней для a и b постоянна и равна n.

П р и м е р 1 .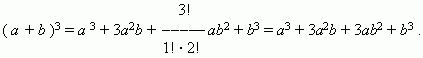

( См. формулу суммы кубов двух чисел ).

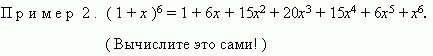
Числа 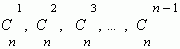называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

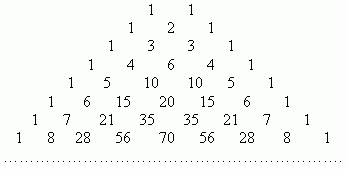
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

( a + b )⁷ ,

мы можем получить результат моментально, используя таблицу:

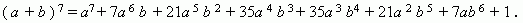
Свойства биномиальных коэффициентов.

1.Сумма коэффициентов разложения ( a + b ) ⁿ равна 2 ⁿ .

Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

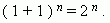
2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

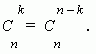
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

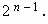
Для доказательства воспользуемся биномом: 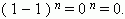Здесь чётные члены имеют знак « + » , а нечётные - « - ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: 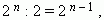что и требовалось доказать.

События

Событие. Элементарное событие.

Пространство элементарных событий.

Достоверное событие. Невозможное событие.

Тождественные события.

Сумма, произведение, разность событий.

Противоположные события. Несовместные события.

Равновозможные события.

Под событием в теории вероятностей понимают любой факт, который может произойти или не произойти в результате опыта со случайным исходом. Самый простой результат такого опыта ( например, появление "орла" или "решки" при бросании монеты, попадание в цель при стрельбе, появление туза при вынимании карты из колоды, случайное выпадение числа при бросании игральной кости и т.д.) называется элементарным событием.

Множество всех элементарных событий Е называется пространством элементарных событий. Так, при бросании игральной кости это пространство состоит из шести элементарных событий, а при вынимании карты из колоды – из 52. Событие может состоять из одного или нескольких элементарных событий, например, появление двух тузов подряд при вынимании карты из колоды, или выпадение одного и того же числа при трёхкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий.

Достоверным событием называется всё пространство элементарных событий. Таким образом, достоверное событие – это событие, которое обязательно должно произойти в результате данного опыта. При бросании игральной кости таким событием является её падение на одну из граней.

Невозможным событием ( 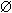) называется пустое подмножество пространства элементарных событий. То есть, невозможное событие не может произойти в результате данного опыта. Так, при бросании игральной кости невозможным событием является её падение на ребро.

События А и В называются тождественными ( А = В ), если событие А происходит тогда и только тогда, когда проиходит событие В .

Говорят, что событие А влечёт за собой событие В ( А 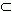В ), если из условия "произошло событие А" следует "произошло событие В".

Событие С называется суммой событий А и В ( С = А 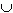В ), если событие С происходит тогда и только тогда, когда происходит либо А , либо В.

Событие С называется произведением событий А и В ( С = А В ), если событие С происходит тогда и только тогда, когда происходит и А , и В.

Событие С называется разностью событий А и В ( С = А – В ), если событие С происходит тогда и только тогда, когда происходит событие А , и не происходит событие В.

Событие А' называется противоположным событию А , если не произошло событие А. Так, промах и попадание при стрельбе – противоположные события.

События А и В называются несовместными ( А В = 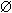) ,если их одновременное появление невозможно. Например, выпадение и "решки", и "орла" при бросании монеты.

Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются равновозможными. Примеры равновозможных событий: появление двойки, туза и валета при вынимании карты из колоды, выпадение любого из чисел от 1 до 6 при бросании игральной кости и т.п.