Другое определение непрерывной случайной величины

Случайная величина называется непрерывной, если её функция распределения есть непрерывная, кусочно-дифференцируемая функция.

Вспомним, что кусочная дифференцируемость означает, что функция состоит из частей, которые являются непрерывно дифференцируемыми, т.е. имеют непрерывную производную. Если график F(x) представляет собой гладкую кривую, без изломов, то функция является дифференцируемой во всей области определения. Если график не имеет разрывов, но имеет изломы (рис.9.2.4,а), то функция кусочно-дифференцируема. В точках излома производная не существует, в этих точках нельзя провести единственную касательную.

a)	б)
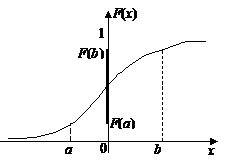Рис.9.2.4

Если функция распределения 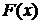на некоторых участках непрерывна, а в отдельных точках имеет разрывы (рис.9.2.3,б), то случайная величина называется смешанной. Например, функция распределения случайной величины - времени Т безотказной работы прибора, испытываемого в течение времени t- непрерывна всюду, кроме точки t. Смешанная случайная величина S- площадь разрушений, наносимых цели бомбой, имеет разрывную функцию распределения.

6.. Если Х – непрерывная случайная величина, то (априорная) вероятность того, что она примет данное конкретное значение, равна нулю:

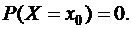(9.2.6)

Замечание.То, что вероятность Р(Х=х₀)=0, не означает, что данное событие невозможно. Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений, в частности, это значение может оказаться равным х₀. Следовательно, нулевой вероятностью могут обладать не только невозможные, но и возможные события, т.е.

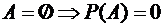, но .

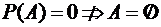Представление о возможном событии с нулевой вероятностью не более парадоксально, чем представление о длине точки. Известно, что длина одной точки равна нулю, тем не менее, длина отрезка, состоящего из многих точек, не равна нулю.

Пример 1.Вероятность того, что выточенная деталь примет строго заданные размеры, равна 0. На практике значение любой физической величины можно измерить лишь с некоторой точностью, а абсолютно точное значение физической величины есть лишь математическая абстракция. Однако можно определить вероятность того, что размеры деталей не выйдут за дозволенные границы.

7.Обобщение свойства 5 для непрерывной случайной величины.

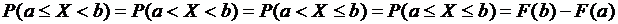. (9.2.8)

Примеры функций распределения

Пример 1. Функция распределения случайной величины Х задана аналитически следующим образом:

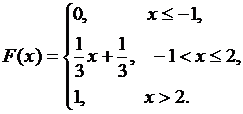
Построить график и найти вероятность того, что в результате испытания Х примет значение, заключенное в промежутке [0,1).

Решение. По формуле (9.2.5)

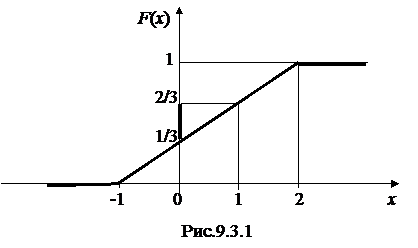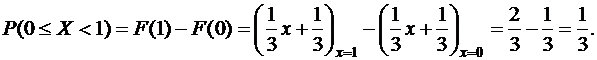
Геометрически это означает длину отрезка F(1)-F(0) на оси ординат (рис.9.3.1). По виду графика и по аналитическому выражению функции распределения можно определить, что значения случайной величины Х сосредоточены на промежутке [-1; 2). Кроме того, видно, что F(х) является непрерывной и кусочно-дифференцируемой функцией. В точках -1 и 2 функция не дифференцируема. На оси ординат отмечена вероятность попадания случайной величины в промежуток [0,1).

Пример 2. Случайная величина Х- проекция радиус-вектора случайной точки окружности радиуса а на диаметр - имеет функцию распределения (закон арксинуса, рис.9.3.2,а):

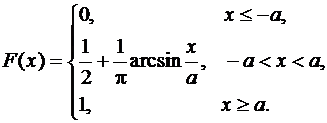
а)	б)
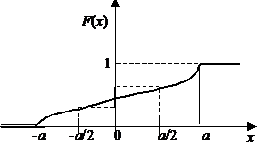Рис.9.3.2

Построить график и найти вероятность того, что Х окажется в пределах промежутка .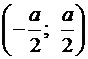

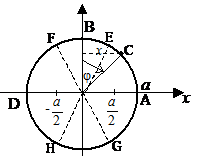
Решение. Здесь значения случайной величины сосредоточены на промежутке (-а; а)(рис.9.3.2,б). - это угол, отсчитываемый вправо и влево от оси ординат. Рассмотрим функцию распределения в нескольких точках, изображенных на чертеже.

а)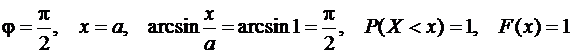

(все значения случайной величины сосредоточены на ).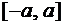

б)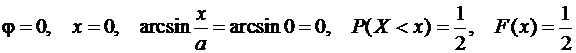

(левая половина окружности).

с)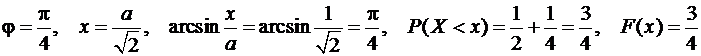

(слева ¾ окружности).

d) .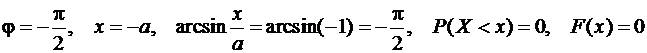

По формуле (9.2.5)

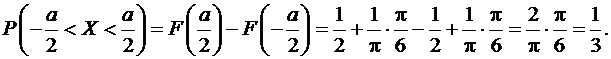
В промежуток 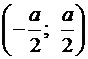могут попасть точки дуг FE и HG, каждая из которых содержит 60°, в сумме 120° (2p/3 радиан). Геометрически эта вероятность тоже равна .

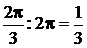Пример 3. .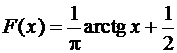

Построить график. Найти вероятность попадания случайной величины в промежутк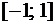и и .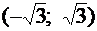

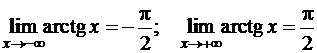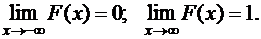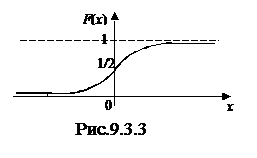
Здесь возможные значения ХÎ(-¥;+¥), т.е. принимают любые действительные значения. Как известно, Тогда Кроме того, из аналитического задания функции следует, что 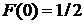. График приведен на рис. 9.3.3.

.

.

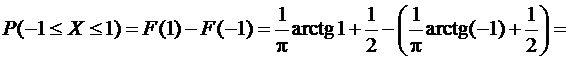
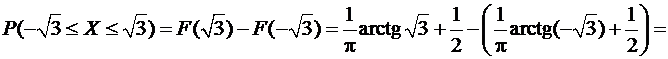
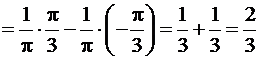В предыдущих примерах рассматривались непрерывные случайные величины. Однако интегральная функция распределения имеет смысл и для дискретной случайной величины.

Пример 4. Построить функцию распределения для характеристической случайной величины c_k(индикатора события).

ck
p	q	p

Закон распределения c_k:

Выясним значения функции распределения на различных участках числовой оси.

1) 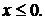Вероятность того, что c_k примет значение, меньшее 0, т.е. попадёт в промежуток (-¥; х), равна 0 (см. таблицу распределения) Þ

Р(c_k<x)=P(-¥<c_k<x)=F(x)=0.

2) 0<x£1. Случайная величина может принять только одно возможное значение, меньшее х, из этого промежутка: c_k =0. Вероятность этого события равна

qÞF(x)=q.

3) 1<x£¥. Все значения случайной величины c_k (0 и 1) меньше любого х из этого промежутка Þ событие c_k<x для этих х является достоверным,

Р(c_k<x)=1.

Функция распределения аналитически может быть записана так:

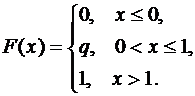
На рис. 9.3.4 показан график интегральной функции распределения. График можно построить быстрее, если воспользоваться свойством 4. Для индикатора события возможные значения случайной величины, а именно 0 и 1, сосредоточены на промежутке [0, 1] Þ для x<0F(x)=0, дляx>1F(x)=1. Легко проверить, что для такой функции выполняются все свойства функции распределения. Особо отметим свойство 3 – непрерывность слева, что наглядно выражено на графике.

Функция распределения дискретной случайной величины не является элементарной функцией. Это – ступенчатая функция, имеющая конечное или бесконечное (счётное) число разрывов первого рода. Такие функции называются кусочно-постоянными.

Пример 5. Производится три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4 (например, три выстрела по мишени, А- попадание при одном выстреле). Рассматривается случайная величина Х – число появлений события А в трёх опытах. Построить ряд распределения и функцию распределения.

Случайная величина Х имеет биномиальное распределение. Для построения ряда распределения вычислим вероятности по формуле Бернулли:

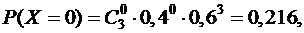и.т.д.

хi
pi	0,216	0,432	0,288	0,064

Для x<0 и x>3 сразу напишем значения F(x):

F(x)=0 для x<0 и F(x)=1для x>3, т.к. все возможные значения сосредоточены на промежутке [0; 3]. Разобьём оставшийся промежуток на части:

1) .

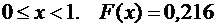2) 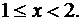Возможные значения Х, меньшие х из этого промежутка, равны 0 или 1.

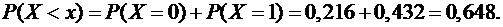
3)

.

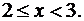
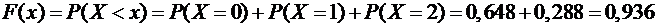Таким образом,

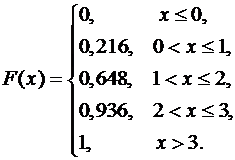
График функции распределения приведён на рис.9.3.5. Рис.9.3.5

Тема: Плотность распределения

Плотность распределения

(дифференциальная функция распределения)

Другим видом функциональной зависимости между возможными значениями случайной величины и вероятностями их принятия является плотность распределения. Понятие плотности распределения имеет смысл только для непрерывных случайных величин, т.е. имеющих непрерывную и кусочно-дифференцируемую интегральную функцию распределения.

Определение.Плотностью распределения, или дифференциальной функцией распределения называется производная от интегральной функции распределения:

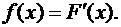(10.1)

Если F(x) непрерывно дифференцируема, то плотность непрерывна, если F(x) кусочно-дифференцируема, то плотность может иметь разрывы первого рода (в точках разрыва производной).