Понятие о нер-ве с 1й переменной и мн-ве его решений. Равносильные нер-ва. Теоремы о равносильных нер-вах.

(Напр 1-х 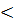3х-2,х 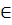Х – это предложение явл предикатом, такие предикаты наз-т нер-ми с 1й переменной). Предикатом вида f(х) 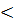g(х) или f(х) 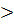g(х) заданный на мн-ве х наз-ся нерав-м с 1й переменной. Мн-вом решений нер-ва f(х) 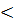g(х) заданным на мн-ве х наз мн-во истинности этого предиката, а каждый элемент этого мн-ва наз-ся решением нер-ва. Значение перемен-й х=а, при кот нер-во превращается в истинное числовое нер-во назыв его решением. Если кажд решение 1го нер-ва явл решением 2го нер-ва, то 2-е нер-во наз следствием 1го.

2 нер-ва наз равносильными, если их мн-во решений совпадают.

Теорема 1 о равносильности нер-в. Если в каждой части нер-ва f(х) 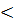g(х) заданного на мн-ве прибавить одно и тоже выражение с переменной h(x), x 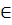Х, то получим нер-во f(x)+h(x)=g(x)+h(х) равносильное исходному. Следствие из теоремы: 1) если к каждой части нер-ва прибавить одно и тоже число, то получим нер-во равносильное данному; 2) члены нер-ва м переносить из 1й части в другую с противопол-м знаком.

Теорема 2 Если обе части нер-ва f(х) 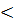g(х) заданного на мн-ве х умножить на одно и тоже выражение с переменной h(x) заданное на томже мн-ве х и положит-е на нем, то получим нер-во f(x)*h(x) 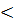g(x)*h(х) равносильное исходному. Следствие из теоремы: если обе части нер-ва умножить на одно и тоже положит-е действительное число, то получим нер-во равносильное данному.

Теорема 3 Если обе части нер-ва f(х) 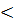g(х) заданного на мн-ве х умножить на одно и тоже выраж-е с переменной h(х) заданного на том же мн-ве х и отрицательное на нем, то получим нер-во f(x)*h(x) 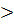g(x)*h(х) равносильно данному. Следствие: если обе части нер-ва умножить на одно и тоже отрицат-е действ-е число и при этом знак нер-ва поменять на противопол-й, получим нер-во равносильное данному.

10. Бинарные отношения м/у элементами 2х мн-в, сп-бы из задания. Виды отношений м/у элементами 2х мн-в.

Бинарным соответствием м/у элем-ми мн-в х и у наз любое ( декартово произ-е этих мн-в. Обознач-ся больш буквами лат алфавита, обычно не первые а кот стоят в конце алфавита (R,S,T..). для задания соответствия м/у элементами мн-в х и у надо указать ( дек-во произв-е х и у – это подмн-во обознач-ся Г. Соответствие – упорядоченная тройка мн-в, где (Х, У, Г), где Г(х*у. если а и b элементы мн-в Х; У, т. е. а 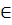х, b 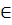у и элемент а наход-ся в соответствии R с элементом b, то это запис-ся- aRb, (a,b) 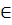R(элемент а наход-ся в соотв-и Rс элементом b). Мн-во х наз-ся мн-ом отправления соответствия R, а мн-во у мн-ом прибытия соответст-я R. Мн-во 1х компонентов пар, кот 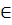соответ-ю R наз областью опред-ия соответствия, а мн-во др компанентов пар наз мн-ом значений соответствия. Т. к. соотв-е это мн-во, то его м задать теми же сп-ми, что и любое мн-во . 1) Если мн-во х и у конечные, то соотв-е м задать перечислением. Форма записи пар м/б различной: а) в виде мн-ва; б) таблицы; в) графа; в виде рисунка, в кот мн-во х и у показывают авалами. Элементы мн-в х и у обозн-т авалами, элементы обозн-т точками, а соответствие стрелками. 2) указание характеристич-го св-ва всех пар, кот 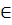соответствию R. 3) если мн-во х и у числовые, то соответствие м/у элементами этих мн-в м задать при помоши графика на координатной пл-ти. Соответствие R наз полным, если график Г совпадает с декартовым * мн-в (х;у) (Г=х;у). Если график соответствия R есть пустое мн-во, то соответствие R наз пустым. Соответствием, обратным соответствию R м/у элементами мн-в (х;у) наз соответствие 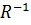м/у мн-ми у и х такое, что У 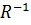Х тогда и т т , к х R у. для того, чтобы получить обратное соответв-е необходимо поменять местами компаненты пар. Для того, чтобы построить граф обратного соответствия достаточно поменять направление всех стрелок в графе в соответст-и с R. Если мн-во х и у числовые, то графики соответст-я R 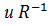симметричны относительно биссектрисы 1го и 3го координат-х углов. Соответст-е, график кот явл дополнение-м графика соответст-я R до декарт-во * мн-в х и у наз противопол-м для соответст-я R и обознач-ся 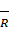. соответст-я 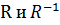наз взаимнопротивопол-м. Графики взаимнопротивопол-м соответствий не пересекаются, а их объединения есть мн-ва.