Однородные линейные ДУ n-го порядка. Две теоремы о свойствах решений ОЛДУ (док.)
1) Если у1(х) – решение ЛОДУ у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0 (2) , то функция С у1(х), где С=const, также является решением этого ЛОДУ.
 Док-во:
Док-во:
Су(n) + P1Сy(n-1) +…+ Pn-1 С y’ + Pn С y = 0
С(у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y ) = 0
у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0
2) Если у1(х) и у2(х) – решение ЛОДУ (2), то функции у1(х) + у2(х) также являются решениями этого ДУ
Док-во:
(у1+у2)(n) + P1(у1+у2) (n-1) +…+ Pn-1 (у1+у2)’ + Pn (у1+у2) =
= [у1 (n) + P1 у1 (n-1) +…+ Pn-1 у1’ + Pn у1] + [у2 (n) + P1 у2 (n-1) +…+ Pn-1 у2’ + Pn у2] = 0
51. Определитель Вронского. Теорема о равенстве нулю вронскиана линейно-зависимых функций (док.).
Определение:
C1y1(x0) + C2y2(x0) + … + Cnyn(x0) = y0
C1y1’(x0) + C2y2’(x0) + … + Cnyn’(x0) = y0’
…………………………………………..
C1y1(n-1)(x0) + C2y2(n-1)(x0) + … + Cnyn(n-1) (x0) = y0(n-1)
(, где y1, y2, yn - ФСР C1 ,C2 ,…,Cn- const)
Определителем этой системой является определитель Вронского
Теорема: (Необходимое условие линейной зависимости функции, но не являются достаточным)
Если функции y1, y2, … ,yn - линейно зависимы, то их определитель Вронского тождественно равен 0.
Док-во:
Т.к. y1, y2, … ,yn - линейно зависимы, то
α1y1 + α2y2 + …+ αnyn = 0 на (a,b),
какое-то αi ≠ 0
продифференцируем равенство (n-1) раз и получим линейную однородную систему уравнений
 α1y1 + α2y2 + …+ αnyn = 0
α1y1 + α2y2 + …+ αnyn = 0
α1y1’ + α2y2’ + …+ αnyn’ = 0
α1y1’’ + α2y2’’ + …+ αnyn’’ = 0 =>
……………………………..
α1y1(n-1) + α2y2(n-1) + …+ αnyn(n-1) = 0
ð эта теорема имеет нетривиальное решение любых Х из (а,b), определитель этой системы – определитель Вронского.
W[y1, y2, … ,yn ] = 0 для любых Х из [а,b]
52. Теорема о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ
( док.).
Если n решений y1, y2, … ,yn ЛОДУ у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0 линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х 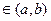 | для любого Х из (а,b) .
| для любого Х из (а,b) .
Следствие:
Определитель Вронского системы уравнений [y1, y2, … ,yn ] , где yi – решение ЛОДУ (2), либо 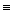 0, если система линейно-зависима.
0, если система линейно-зависима.
53. Теорема о структуре общего решения ЛОДУ (док). Понятие ФСР.
Опр: фундаментальной системы решений (ФСР) -система n линейно-зависимого решения ЛОДУ n-го порядка называется ее ФСР
Теорема о структуре общего решения ЛОДУ
Если функции y1(х), y2(х), … ,yn(х) – образует ФСР ЛОДУ у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0 , то y(х) = C1y1(x) + C2y2(x) + … + Cnyn(x) = 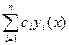 , есть общее решение этого уровня. (4).
, есть общее решение этого уровня. (4).
Док-во:
Из теоремы о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ:
Если n решений y1, y2, … ,yn ЛОДУ (2) и они линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х 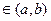 | для любого Х из (а,b) .
| для любого Х из (а,b) .
ð что (4) являются решением у(n) + P1y(n-1) +…+ Pn-1 y’ + Pn y = 0
остается доказать, что можно подобрать const-ты то С1, С2, … Сn , таким образом что функция (4) удовлетворяет любой системе начальных условий [н.у.]
Задаем н.у. , при x0 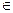 (а,b) y(х0) = y0, y’(х0) = y0’, y(n-1) (x0) = y0(n-1) определяем C1,C2,…, Cn
(а,b) y(х0) = y0, y’(х0) = y0’, y(n-1) (x0) = y0(n-1) определяем C1,C2,…, Cn
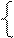 Определение:
Определение:
C1y1(x0) + C2y2(x0) + … + Cnyn(x0) = y0
C1y1’(x0) + C2y2’(x0) + … + Cnyn’(x0) = y0’ , где y1, y2, yn ФСР C1 C2 Cn const
………………………………………….. (5)
C1y1(n-1)(x0) + C2y2(n-1)(x0) + … + Cnyn(n-1) (x0) = y0(n-1)
Определителем этой системы является определитель Вронского
W[y1, y2, … ,yn] 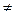 0, C1,C2,…, Cn - определяется един-м образом
0, C1,C2,…, Cn - определяется един-м образом
Построим 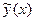 = C1y1(x) + C2y2(x) + … + Cnyn(x) ,
= C1y1(x) + C2y2(x) + … + Cnyn(x) ,
согласно свойству (если y1) α1y1 + α2y2 + …+ αnyn = 0 причем хотя бы одно hi 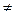 0.
0.
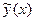 - является решением ДУ(2)
- является решением ДУ(2) 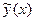 = y(x) , т.к. система (5) определена теми же н.у., что и y(x) ч.т.д.
= y(x) , т.к. система (5) определена теми же н.у., что и y(x) ч.т.д.
Следствие:
1) максимальное число линейно-независимых решение ЛОДУ, коэффициенты непрерывны на (a,b) равно порядку этого уравнения.
2) независимо от н.у. все другие решения таких уравнений ЛОДУ является линейной комбинацией этих независимых решений (решений ФС)
3) Пространство решений ЛОДУ n-го порядка имеет базис из n-векторов, т.е. пространство n-мерное.
4) Для решения ЛОДУ n-го порядка необходимо найти ФСР. Общее решение получается как линейная комбинация решений ФС.
