Метод равносильных переходов
Методы решения
логарифмических неравенств
(задания С3 ЕГЭ)
Корянов А.Г., Прокофьев А.А.
Основой для написания данной статьи явился анализ заданий материалов МИОО, предлагавшихся в течение двух лет в качестве подготовки к итоговому экзамену, и результаты проверки авторами в качестве экспертов работ ЕГЭ 2010 и 2011 гг.
Надо отдать должное составителям заданий, поскольку при решении логарифмических неравенств в заданиях С3 в диагностических, тренировочных, репетиционных работах и в итоговых вариантах ЕГЭ 2010 и 2011 в основном было достаточно использования стандартных методов. К таковым методам можно отнести:
· метод равносильных переходов;
· решение неравенства на промежутках;
· метод замены;
· обобщенный метод интервалов;
Кроме того, в ряде репетиционных работ для решения неравенств использовались нестандартные методы:
· метод рационализации;
· метод оценки, в частности, использование классических неравенств.
Остановимся на перечисленных выше методах решения.
Метод равносильных переходов
При решении неравенств используют преобразования, при которых множество решений неравенства либо не меняется, либо расширяется (можно получить посторонние решения). Поэтому важно знать, какие преобразования неравенства являются равносильными и при каких условиях.
Начнем с примеров, в которых используются логарифмы с постоянными основаниями.
неравенства вида 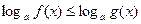
Пусть логарифмическое неравенство удалось свести к виду
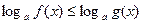 ,
,
тогда для дальнейшего решения применяется одна из схем.
Если число 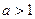 , то
, то
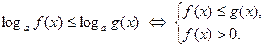 (1)
(1)
Если число 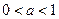 , то
, то
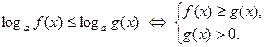 (2)
(2)
При выводе этих схем решения неравенства используется свойство монотонности функции 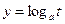 на множестве
на множестве 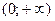 . При
. При 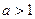 функция возрастающая, при
функция возрастающая, при 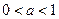 – убывающая.
– убывающая.
Замечание. При решении строгого неравенства 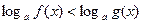 в схемах (1) и (2) нестрогие неравенства заменяются строгими.
в схемах (1) и (2) нестрогие неравенства заменяются строгими.
Пример 1. Решить неравенство
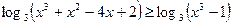 .
.
Решение.Так как функция 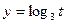 строго возрастает на множестве
строго возрастает на множестве 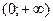 , то данное неравенство можно заменить равносильной системой
, то данное неравенство можно заменить равносильной системой
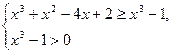
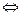
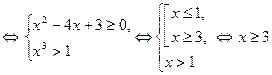

Ответ: 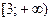 .
.
Рассмотрим неравенства, в которых присутствуют логарифмы с переменным основанием.
неравенства вида 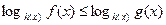
Из предыдущего пункта следует, что неравенство указанного вида равносильно совокупности систем неравенств.
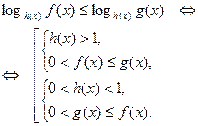 (3)
(3)
Замечание. При решении строгого неравенства 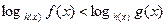 в схеме (3) нестрогие неравенства заменяются строгими.
в схеме (3) нестрогие неравенства заменяются строгими.
Пример 2.Решить неравенство
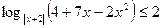 .
.
Решение. Запишем неравенство в виде
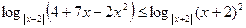
и заменим его равносильной совокупностью двух систем
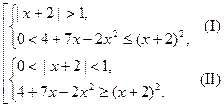
 Решим систему (I):
Решим систему (I): 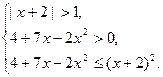 Имеем
Имеем 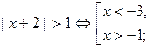
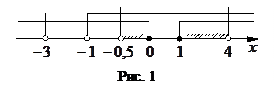
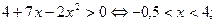
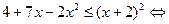
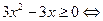
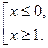
Отсюда получаем (см. рис. 1) решение (I):
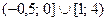 .
.
Решим систему (II): 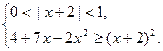
Имеем 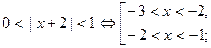
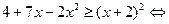
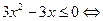
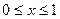 .
.
Получаем, что система (II) решений не имеет.
Ответ: 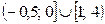 .
.
Пример 3. (МИОО,2009).Решить неравенство
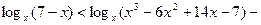
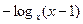 .
.
Решение. Выполняя равносильные переходы, получим, что данное неравенство равносильно следующей системе неравенств
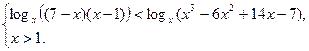
Необходимо рассмотреть только случай, когда основание больше единицы, поэтому полученная система равносильна следующей
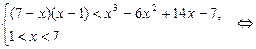
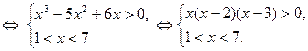
На рис. 2 представлена графическая интерпретация получения решения последней системы неравенств.
Ответ: 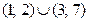 .
.
неравенства вида
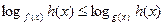
В общем случае в неравенствах данного вида логарифмы приводят к одному числовому основанию 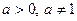 , переходя к равносильному неравенству
, переходя к равносильному неравенству
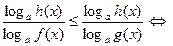
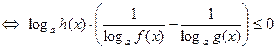 .
.
Пример 4. (МИОО, январь 2010).Решить неравенство
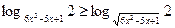 .
.
Решение. Данное неравенство равносильно неравенству:
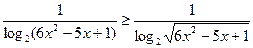 .
.
Используя замену 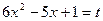 , где
, где 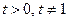 , получим
, получим
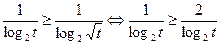 .
.
Отсюда получаем 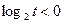 или
или 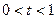 . Выполнив обратную замену, имеем
. Выполнив обратную замену, имеем 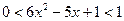 .
.
Решая неравенство 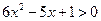 , получаем значения
, получаем значения 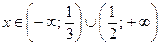 .
.
Неравенство 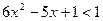 имеет решения
имеет решения 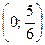 . Следовательно, решением исходного неравенства является множество
. Следовательно, решением исходного неравенства является множество 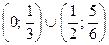 .
.
Ответ. 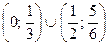 .
.
Пример 5.Решить неравенство
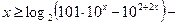
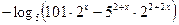 .
.
Решение. Используя тождество 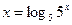 , выполняя равносильные преобразования, преобразуем исходное неравенство:
, выполняя равносильные преобразования, преобразуем исходное неравенство:
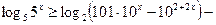
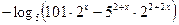 ,
,
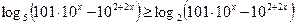 .
.
Используя замену 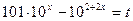 , где
, где 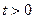 , получаем неравенство
, получаем неравенство
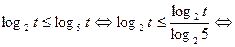
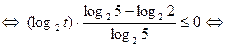
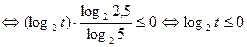 .
.
Отсюда имеем 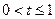 .
.
Выполняя обратную замену, имеем
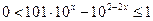 .
.
Пусть 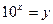 . Тогда решая систему
. Тогда решая систему
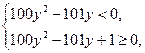
получим с учетом 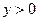 , что значения
, что значения 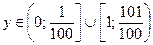 .
.
Выполним обратную замену
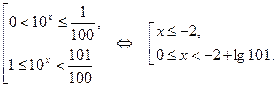
Ответ. 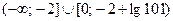 .
.
Приведем другой способ решения неравенств рассматриваемого вида.
Для этого исследуем функцию 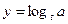 , где переменная
, где переменная 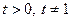 и число
и число 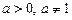 . Так как
. Так как
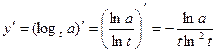 ,
,
то при 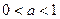 функция
функция 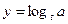 возрастает на каждом из промежутков
возрастает на каждом из промежутков 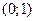 и
и 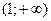 , при
, при 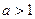 функция
функция 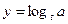 убывает на каждом из промежутков
убывает на каждом из промежутков 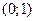 и
и 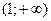 .
.
Отметим, что при 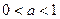 функция
функция 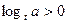 при
при 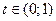 и
и 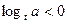 при
при 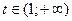 , при
, при 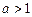 функция
функция 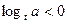 при
при 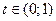 и
и 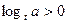 при
при 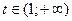 .
.
Из этих рассуждений следует, что строгое неравенство
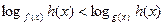
равносильно совокупности двух систем:
(I) 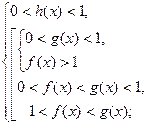
(II) 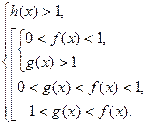
Для нестрого неравенства 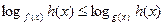 в представленной выше совокупности неравенства
в представленной выше совокупности неравенства 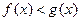 и
и 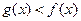 заменяются на нестрогие и совокупность содержит еще следующую систему
заменяются на нестрогие и совокупность содержит еще следующую систему
(III) 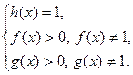
Пример 6.Решить неравенство
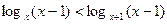 .
.
Решение.Данноенеравенство равносильно совокупности систем
(I) 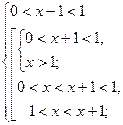 и (II)
и (II) 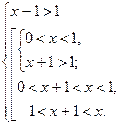
Система (I) имеет решения 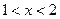 . Система (II) не имеет решений.
. Система (II) не имеет решений.
Ответ: 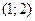 .
.
Использование формул
Наибольшее число ошибок при решении задания С3 в ЕГЭ 2010 и 2011 возникло в результате неправильного использования формул:
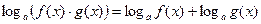 (4)
(4)
и
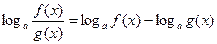 , (5)
, (5)
где 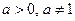 ,
, 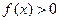 и
и 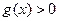 .
.
Заметим, что равенства (4) и (5) в общем случае не являются тождествами, поскольку области определения левой и правой частей равенства могут не совпадать. Так в левой части равенств (4) и (5) выражение будет определено при таких значениях 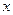 , когда и
, когда и 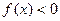 и
и 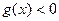 . Правая часть при таких значениях
. Правая часть при таких значениях 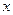 не имеет смысла.
не имеет смысла.
Формулы (4) и (5) используются как для преобразования логарифма произведения (частного) в сумму (разность) логарифмов соответственно, так и в обратную сторону.
В общем случае переход слева направо может привести к потере решений. Если даны выражения 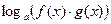 или
или 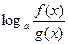 и есть желание преобразовать их в сумму или разность логарифмов, равносильный переход выглядит так
и есть желание преобразовать их в сумму или разность логарифмов, равносильный переход выглядит так
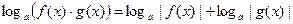
и
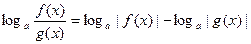 .
.
В общем случае переход справа налево может привести к приобретению посторонних решений. Однако эти посторонние решения могут быть исключены, как не входящие в область определения переменной исходного выражения.
Пример 7 (ЕГЭ-2011). Решить неравенство
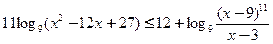 .
.
Решение (предложенное в критериях).
1-й способ. Значения 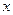 , при которых определены обе части неравенства, задаются условиями
, при которых определены обе части неравенства, задаются условиями
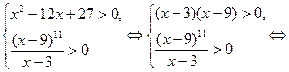
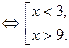
Для таких 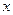 получаем
получаем
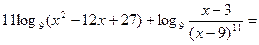
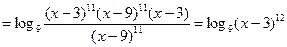 .
.
Исходное неравенство примет вид
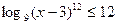 .
.
Так как 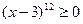 , то при
, то при 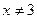 имеем:
имеем:
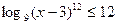
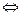
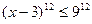
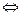
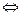
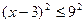
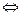
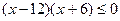 .
.
Откуда значения 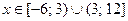 .
.
Учитывая область определения исходного неравенства 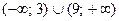 , получим в ответе множество
, получим в ответе множество 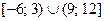 .
.
Решение. 2-й способ. Область определения данного неравенства – есть множество 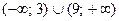 . Для таких
. Для таких 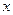 исходное неравенство приводится к виду:
исходное неравенство приводится к виду:
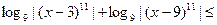
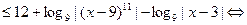
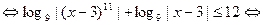
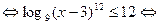
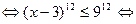
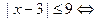
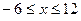 .
.
Учитывая, что значения 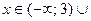
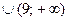 , получим ответ
, получим ответ 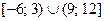 .
.
Ответ: 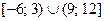 .
.
Комментарий.Большинство выпускников использовало 2-й способ. При этом массово забывали о необходимости использования модулей.
Иногда в логарифмических неравенствах присутствуют логарифмы с разными основаниями. В этом случае часто для последующего решения привести их к одному основанию, используя формулу перехода к другому основанию:
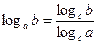 , (6)
, (6)
где 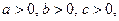
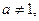
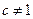 .
.
Пример 8. (ЕГЭ 2010).Решить неравенство
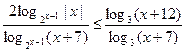 .
.
Решение. В соответствии с определением логарифма, входящие в неравенство выражения имеют смысл при выполнении условий:
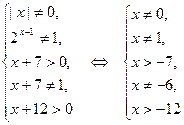
Отсюда получаем значения
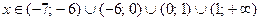 .
.
Так как при допустимых значениях переменной 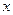 по свойствам логарифма справедливы равенства:
по свойствам логарифма справедливы равенства:
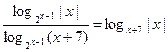
и
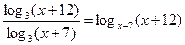 ,
,
то исходное неравенство приводится к виду
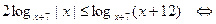
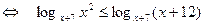 .
.
Последнее неравенство равносильно совокупности двух систем на множестве
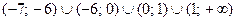 :
:
(I) 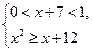 и (II)
и (II) 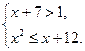
Для системы неравенств (I) имеем:
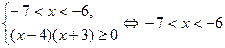 .
.
Для системы неравенств (II) имеем:
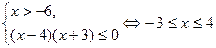 .
.
С учетом области определения данного неравенства получаем ответ.
Ответ: 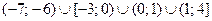 .
.
Расщепление неравенств
Названный метод применяется для решения неравенств вида 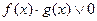 или
или 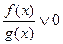 , где символ
, где символ 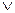 означает один из знаков неравенств
означает один из знаков неравенств 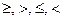 . Например,
. Например,
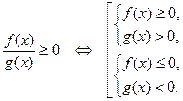 (7)
(7)
Пример 9. Решить неравенство
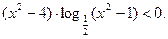
Решение.Данноенеравенство равносильно совокупности систем (I) и (II):
(I) 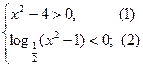
(II) 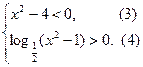
Решим каждое неравенство системы (I). Для неравенства (1) имеем:
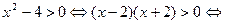
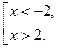
Для неравенства (2) имеем:
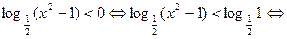
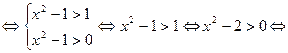
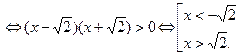
Значит все 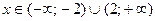 – решения системы (I).
– решения системы (I).
Найдем решение системы (II). Для неравенства (3) имеем:
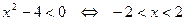 .
.
Для неравенства (4) имеем:
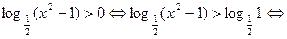
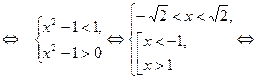
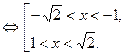
Значит все 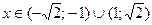 – решения системы (II).
– решения системы (II).
Объединяя решения систем (I) и (II), получаем ответ.
Ответ: 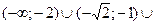
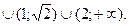
Воспользуемся рассмотренным методом и для решения следующего неравенства.
Пример 10. (ЕГЭ 2011).Решить неравенство 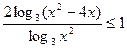 .
.
Решение. Значения 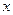 , при которых определены обе части неравенства, задаются условиями
, при которых определены обе части неравенства, задаются условиями
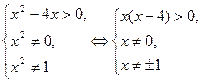
Отсюда находим значения
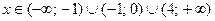 .
.
Для таких 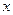 получаем, что исходное неравенство равносильно следующему
получаем, что исходное неравенство равносильно следующему
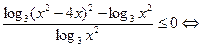
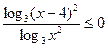 .
.
Последнее неравенство, а значит и исходное, равносильно совокупности двух систем.
(I) 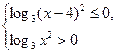 и (II)
и (II) 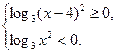
Рассмотрим систему (I). По свойству возрастающей функции 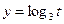 на промежутке
на промежутке 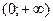 получаем
получаем
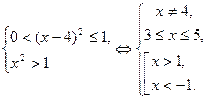
Отсюда имеем значения 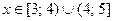 .
.
Учитывая полученные выше ограничения, получаем решения системы (I): 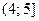 .
.
Рассмотрим систему (II). Аналогично предыдущему получаем
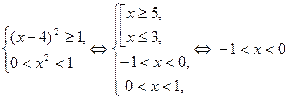 .
.
Объединяя найденные решения, получаем значения 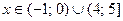 .
.
Ответ: 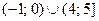 .
.
