Понятие мн-ва. Отнош-я м/у мн-ми. Операции пересеч и объед мн-в, законы этих операций.
Понятие об уравнении с 1-й переменной и мн-ве его решений. Равноильные уравнения. Теоремы о равносильных уравнениях.
Пусть f(х) и g(х)-выражения с 1й переменной, заданные на мн-ве х предикатами вида f(х)=g(х), заданный на мн-ве х наз-ся уравнением с 1й переменной. (напр. 2х+3=3х-8,х 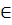 R).корнем уравнения наз-ся значение переменной из области определения при кот ур-ие преврашается в верное числовое равенство. Решить уравнение, значит найти мн-во корней этого уравнения. Уравление
R).корнем уравнения наз-ся значение переменной из области определения при кот ур-ие преврашается в верное числовое равенство. Решить уравнение, значит найти мн-во корней этого уравнения. Уравление 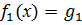 (х) явл следствием уравн-я
(х) явл следствием уравн-я 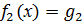 (х), если мн-во корней 2-го уравн-я явл подмн-м мн-ва корней 1-го уравн-я или уравн-е
(х), если мн-во корней 2-го уравн-я явл подмн-м мн-ва корней 1-го уравн-я или уравн-е 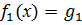 (х) явл следствием уравн-я
(х) явл следствием уравн-я 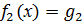 (х), если каждый корень 2-го уравн-я явл корнем уравн-я 1-го.
(х), если каждый корень 2-го уравн-я явл корнем уравн-я 1-го. 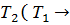 (2)
(2) 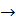 (1).
(1).
Теорема 1 о равенстве уравн-й и следствия из них. Если к каждой части уравн-я n f(х)=g(х) заданных на мн-ве х, прибавить одно и тоже выражение с переменной, n(x), заданное на том же мн-ве х, то получим уравн-е f(x)+h(x)=g(x)+h(х) равносильно данному. Следствие из теорем: 1) к каждой части уравн-я м прибавить одно и тоже число; 2) слагаемы в уравн-и м переносить из одной части уравн-я в другую с противоположным знаком.
Теорема 2. Если каждую часть уравн-я f(х)=g(х) заданного на мн-ве х умножить на одно и тоже выражение h(x) заданного на томже мн-ве х и не равно 0, то получим уравнение f(x)*h(x)=g(x)*h(х) равносильно первому. Следствие: обе части уравн-я м умножить или разделить на одно и тоже число, отличное от нуля.
Понятие мн-ва. Отнош-я м/у мн-ми. Операции пересеч и объед мн-в, законы этих операций.
Мн-во- совок-ть объектов, предметов и понятий, которы объеденены на основании какого-нибудь признака(множ.натур чисел, множ. треугольников, множ.участников класса). Объекты из кот состоят мн-ва – наз-ся его элементами. Мн-во обозначают большими буквами лат алфавита: А,B,C,D, а его элементы – малыми: a,b,c,d. Мн-во, кот не содержит ни 1-го элемента наз пустым (обозн.Ǿ). Мн-ва быв-т конеч-е(множ.однозначных чисел), бескон-е(множ.натуральных чисел, целых чисел, действительных ч.) и не имеет ни одного элемента(множ.действительных корней уровнения 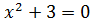 .)
.)
Отношения мн-ва: 1) пересеч-я (если элементы принадлежат к 1-му и 2-му мн-ву одновр-но); 2) включения (подмножество, если каждый элемент 1-го мн-ва явл элементом 2-го мн-ва); 3) равенства (если 2 мн-ва состоят из одних и тех же элементов).
2 множ.наз.равными если они содержат одни и теже элементы. множ В наз. по множ. множ. Аесли каждый элемент мнлж. В является также и элементом множ. А, обозначают В с А
(В с А 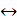 х є В
х є В 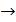 х є А). Пустое множ.явл.подмножеством любого множества. Любое множество является подмножеством самого себе. Ǿ с А; А с А. Если множ.не имеет общих элементов, то говорят что они не пересекаются. Если множ.имеет хотябы один общий элимент, то они пересекаются. Любое множ.можно показывать графически при помощи кругов Эйлера или диограмм Венна.
х є А). Пустое множ.явл.подмножеством любого множества. Любое множество является подмножеством самого себе. Ǿ с А; А с А. Если множ.не имеет общих элементов, то говорят что они не пересекаются. Если множ.имеет хотябы один общий элимент, то они пересекаются. Любое множ.можно показывать графически при помощи кругов Эйлера или диограмм Венна.
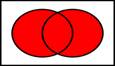
Мн-во наз-ся универсальным, если все мн-ва явл его подмнож-ми. Пересеч-м мн-в А и В наз-ся мн-во, кот состоит из тех и только тех элементов, кот одноврем-но принадлежат и мн-ву А и мн-ву В (обознач 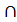 ) Объединением мн-в А и В наз-ся мн-во, кот состоит из тех и только тех элементов, кот входят хотя бы в одно из мн-в А или В. (А
) Объединением мн-в А и В наз-ся мн-во, кот состоит из тех и только тех элементов, кот входят хотя бы в одно из мн-в А или В. (А 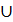 В)
В)
Операции пересечения множеств имеют следующие свойства:
коммутативный (перемест-й) А 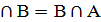 (следует из определения операции пересечения множеств); 2) ассоциативный (сочитательный)
(следует из определения операции пересечения множеств); 2) ассоциативный (сочитательный) 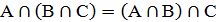 Сочитательный закон позволяет находить пересеч-я и оъед-я 3-х и более мн-в, а также записывать выражения без скобок. 3) дистрибутивный (распределительный)
Сочитательный закон позволяет находить пересеч-я и оъед-я 3-х и более мн-в, а также записывать выражения без скобок. 3) дистрибутивный (распределительный) 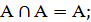
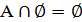 ;
; 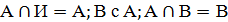
Свойства объединений множеств:
1.коммуникативность 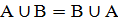 (доказывать следует из объединения множеств)
(доказывать следует из объединения множеств)
2. Ассоциативность 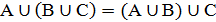 (док. На кругах Эйлера)
(док. На кругах Эйлера)
3. Дистрибутивный: а) 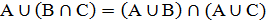 ; б)
; б) 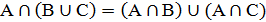
4. 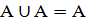
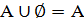
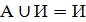
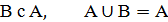
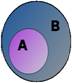 A c B
A c B 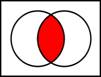 A
A 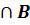
 A
A 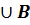
3.Понятие комбинаторной задачи. Правила + и *. Перестановки, размещения без повторений и с повторениями, сочетание без повторений.
Раздел матем-ки, кот рассматр-т задачи,связан-е с комбиниров-мэлементов мн-ва наз-т комбинаторикой. В основе всей теории лежат 2 осн правила: прав-ло суммы и произвед-я. Правило суммы позволяет найти число элементов в объединении 2х или неск-х мн-в, кот не пересек-ся. 1.а) 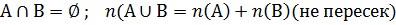 ; б)
; б) 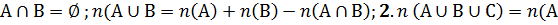 )+n(В)+n(С)-n(А
)+n(В)+n(С)-n(А 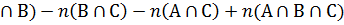
Комбинат-е правило суммы: если выбор одногоэлемента из объединения к не пересекает множество можно выполнить Р1-различными способами,Р2-различными способами, отличных от предыдущ-го и т д, то выбор какого-нибудь одного объкта из все данных объектов к осущ-ть Р1+Р2+…спос-ми.
Правило нахожд-я числа элементов декартово произведения R множеств в мат. наз-ся правилом произведения. 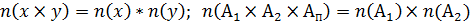
Правило произведения: если первый элимент можно выбрать 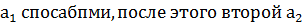 способами и т.д. n-ный после выбора всех предыдущих элиментов можно выбрать
способами и т.д. n-ный после выбора всех предыдущих элиментов можно выбрать 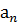 спосабами, то упорядоченную n-ку элементов из всей совокупности можно выбрать
спосабами, то упорядоченную n-ку элементов из всей совокупности можно выбрать 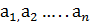 спосабами.
спосабами.
Мн-во наз упорядоч-м,если его элементы расположены в соотв-м порядке. Картежем наз.упорядоченные n-ка элементов. В отличии от картежа в упорядоченном множ.все элементы разные, разные упорядоченные одного и того же множества состоит из одних и тех же элементов и отличаются только порядком элементов. Всевозможные упорядоченные множества составленные из данных n элементов наз. перестановками без повтор-й. Теорема: число СП-в упорядочения n-элем-го мн-ва опред-ся по формуле Рn=n!, где Рn-это число перестановок из n-элементов, n!- n-факториал, n!-произвед-е все N от 1 до n (1, 2, 3… n) (напр. 3! – 1*2*3=6.). Размещение без повторений наз-ся каждое упорядоч-е к-элементное подмн-во данного n-элем-го мн-ва. Теорема:число элементов размещений из n-элем по к-элем опред-ся по формуле. A  =
= 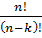 . Сочетанием без повторений наз каждое к-ое подмн-во данного n-элем-го мн-ва обознач-ся Сn. Теорема: кол-во сочетаний без повторений из n-элем по к вычисляется по формуле С
. Сочетанием без повторений наз каждое к-ое подмн-во данного n-элем-го мн-ва обознач-ся Сn. Теорема: кол-во сочетаний без повторений из n-элем по к вычисляется по формуле С 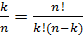 . Кол-во упорядоченных к-элем-х подмн-вданного n-элем-го мн-ва выч-ся по формуле A
. Кол-во упорядоченных к-элем-х подмн-вданного n-элем-го мн-ва выч-ся по формуле A  =
= 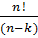 . Тогда кол-во неупоряд-х подмн-в будет в к! раз меньше, чем кол-во упорядоченных т к из каждого неупоряд-го подмн-ва кот содержит к-элементов м составить к-факториал упорядоч-х подмн-в. Т. о. С
. Тогда кол-во неупоряд-х подмн-в будет в к! раз меньше, чем кол-во упорядоченных т к из каждого неупоряд-го подмн-ва кот содержит к-элементов м составить к-факториал упорядоч-х подмн-в. Т. о. С  =
= 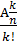 =
= 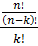 =
= 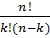 .
.
Размещения с повторениями наз кортеж длины к составленный из k-элементного мн-ва (k м/б 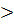 n). Кол-во размещ-й из n-элем по к обозн-ся
n). Кол-во размещ-й из n-элем по к обозн-ся 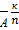 . Теорема: кол-во размещ-й с повторен-ми из n-элем выч-ся по формуле
. Теорема: кол-во размещ-й с повторен-ми из n-элем выч-ся по формуле 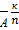 =nk. Перестановки с повтор-ми наз любой кортеж длины n n-элем-го мн-ва. Обозн-ся
=nk. Перестановки с повтор-ми наз любой кортеж длины n n-элем-го мн-ва. Обозн-ся 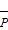 n. Теорема: кол-во различных перестановок с повтор-ми n-элем мн-ва, в кот один из элементов повтор-ся n1 раз, 2-й элемент n2 раз и т д, к-й элемент повтор nk раз вычиисл по формуле
n. Теорема: кол-во различных перестановок с повтор-ми n-элем мн-ва, в кот один из элементов повтор-ся n1 раз, 2-й элемент n2 раз и т д, к-й элемент повтор nk раз вычиисл по формуле 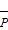 n=
n= 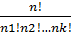 .
.
