Если произведение разделить на один из множителей, то получится другой множитель.
Все остальные таблицы деления получают аналогичным способом.
ПРИЕМЫ ЗАПОМИНАНИЯ ТАБЛИЦЫ ДЕЛЕНИЯ
Приемы запоминания табличных случаев деления связаны со способами получения таблицы деления из соответствующих табличных случаев умножения.
1. Прием, связанный со смыслом действия деления
При небольших значениях делимого и делителя ребенок может либо произвести предметные действия для непосредственного получения результата деления, либо выполнить эти действия мысленно, либо использовать пальцевую модель.
Например: На два окна расставили поровну 10 горшков с цветами. Сколько горшков на каждом окне?
Для получения результата ребенок может воспользоваться любой из упомянутых выше моделей.
При больших значениях делимого и делителя этот прием неудобен. Например: 72 горшка с цветами расставили на 8 окон. Сколько горшков на каждом окне?
Находить результат, используя предметную модель в этом случае неудобно.
2. Прием, связанный с правилом взаимосвязи компонентов умножения и деления
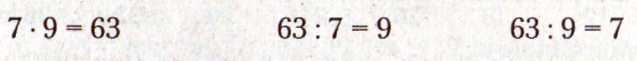В этом случае ребенок ориентируется. На запоминание взаимосвязанной тройки случаев, например:
Если ребенку удается хорошо запомнить один из этих случаев (обычно опорный — это случай умножения) или он может получить его с помощью любого из приемов запоминания таблицы умножения, то используя правило «если произведение разделить на один из множителей, то получится второй множитель», легко получить второй и третий табличные случаи.
№ 13 Методика изучения приема деления двузначного числа на однозначное
При изучении приёма деления двузначного числа на однозначное пользуются правилом деления суммы на число. Рассматриваются группы примеров:
1) 46: 2 = "(40 + 6) : 2=40: 2 +-'6: 2=20 + 3=23 (делимое заменять суммой разрядных слагаемых)
2) 50 : 2= (40 + 10) : 2=40 : 2 + 10 : 2=20 + 5=25 (делимое заменяют суммой удобных слагаемых - круглые числа)
3) 72: 6= (60 +12) : 6=60: 6+ 12: 6= 10 + 2= 12 ( делимое заменяют суммой двух чисел: круглое число и двузначное)
Во всех примерах данные слагаемые будут удобными , если при делении их на данный делитель получаются разрядные слагаемые частного.
В подготовительный период используют упражнения: выделите круглые числа до 100, которые делятся на 2 (10, 20, 40, 60, 80), на 3 (30, 60, 90), на 4 (40, 80) и т. д.; представьте разными способами числа в виде суммы двух слагаемых, каждое из которых делится на данное число без остатка: 24 можно заменить суммой, каждое слагаемое которой делится на 2: 20 + 4, 12 + 12, 10+14 и т. д.; решать разными способами примеры вида: (18 + 45) : 9.
После подготовительной работы рассматриваются примеры трёх групп, при этом обращают большое внимание замене делимого суммой удобных слагаемых и выбору самого удобного способа:
42 : 3= (30+12) : 3=30 : 3+12: 3= 14
42:3=(27+15) :3=27: 3+15 : 3=14 42 :3= (24+1&) : 3 = 24: 3+18:3=14
42 : 3= (36 + 6) : 3=36:3+6: 3=14 и др.
К самому удобному способу можно отнести первый способ, так как при делении удобных слагаемых (30 и 12) получаются разрядные слагаемые частного (10 + 4=14).
Трудными являются примеры вида: 96:4. В таких случаях целесообразно заменить делимое суммой удобных слагаемых, первое из которых выражает наибольшее число десятков, делящееся на делитель: 96: 4= (80+16): 4.
Знания:
1. Разрядный состав числа
2. свойство деления суммы на число
3. Деление числа, оканчивающегося на 0
4. Табличные случая деления
5. «Удобный» состав числа.
Деление с остатком.
Деление с остатком изучается во II классе после завершения работы над внетабличными случаями умножения и деления.
Работа над делением с остатком в пределах 100 расширяет знания учащихся о действии деления, создает новые условия для применения знаний табличных результатов умножения и деления, для применения вычислительных приемов внетабличного умножения и деления, а также своевременно готовит учащихся к изучению письменных приемов деления.
Особенностью деления с остатком по сравнению с известными детям действиями является тот факт, что здесь по двум данным числам — делимому и делителю — находят два числа: частное и остаток.
Дети в своем опыте неоднократно встречались со случаями деления с остатком, выполняя деление предметов (конфет, яблок, орехов и т. д.). Поэтому при изучении деления с остатком важно опираться на этот опыт детей и вместе с тем обогатить его. Полезно начать работу с решения жизненно практических задач. Например: «15 тетрадей раздай ученикам, по 2 тетради каждому. Сколько учеников получили тетради и сколько тетрадей осталось?»
Ученики раздают, раскладывают предметы и устно отвечают на поставленные вопросы.
Наряду с этими заданиями проводится работа с дидактическим материалом и с рисунками.
Делим 14 кружков по 3 кружка. Сколько раз по 3 кружка содержится в 14 кружках? (4 раза.) Сколько кружков остается? (2.) Вводится запись деления с остатком: 14:3=4 (ост. 2). Ученики решают несколько аналогичных примеров и задач, используя предметы или рисунки. Возьмем задачу:" «Мама принесла 11 яблок и раздала их детям, по 2 яблока каждому. Сколько детей получили эти яблоки и сколько яблок осталось?» Ученики решают задачу с помощью кружков .
Решение и ответ задачи записываются следующим образом-11:2=5 (ост. 1).
Ответ: 5 детей и остается 1 яблоко.
Затем раскрывается соотношение между делителем и остатком, т. е. ученики устанавливают: если при делении получается остаток, то он всегда меньше делителя. Для этого сначала решаются примеры на деление последовательных чисел на 2, затем на 3 (4, 5). Например:
10:2=5 12:3 = 4 16:4 = 4
11:2=5(ост.1) 13:3 = 4 (ост. 1) 17:4 = 4(ост 1)
12:2=6 14:3 = 4(ост. 2) 18:4 = 4 (ост. 2)
13:2=6(ост.1) 15:3 = 5 19:4 = 4 (ост. 3)
Учащиеся сравнивают остаток с делителем и замечают, что при делении на 2 в остатке получается только число 1 и не может быть 2 (3, 4 и т. д.). Точно так же выясняется, что при делении на 3 остатком может быть число 1 или 2, при делении на 4 — только числа 1, 2, 3 и т. д. Сравнив остаток и делитель, дети делают вывод, что остаток всегда меньше делителя.
Чтобы соотношение это было усвоено, целесообразно предлагать упражнения, аналогичные следующим:
Какие числа могут получиться в остатке при делении на 5, 7, 10? Сколько различных остатков может быть при делении на 8, 11, 14? Какой наибольший остаток может быть получен при делении на 9, 15, 18? Может ли при делении на 7 получиться в остатке 8, 3, 10?
Для подготовки учащихся к усвоению приема деления с остатком полезно предлагать следующие задания:
Какие числа от 6 до 60 делятся без остатка на б, 7, 9? Какое ближайшее к 47 (52, 61) меньшее число делится без остатка на 8, 9, 6?
Раскрывая общий прием деления с остатком, лучше брать примеры парами: один из них на деление без остатка, а другой 'на деление с остатком, но примеры должны иметь одинаковые делители и частные.
Далее решаются примеры на деление с остатком без примера-помощника. -Пусть надо 37 разделить на 8. Ученик должен усвоить следующее рассуждение: «37 на 8 без остатка не делится. Самое большое число, которое меньше, чем 37, и делится на 8 без остатка, 32. 32 разделить на 8, получится 4; из 37 вычтем 32, получится 5, в остатке 5. Значит, 37 разделить на 8, получится 4 и в остатке 5».
Навык деления с остатком вырабатывается в результате тренировки, поэтому надо больше включать примеров на деление с остатком как в устные упражнения, так и в письменные работы.
Выполняя деление с остатком, учащиеся иногда получают остаток больше делителя, например: 47:5=8 (ост. 7). Чтобы предупредить такие ошибки, полезно предлагать детям неверно решенные примеры, пусть они найдут ошибку, объяснят причину ее появления и решат пример правильно.
ПАМЯТКА
1. подбери число, близкое к делимому, которое меньше его и делится без остатка;
2. раздели это число;
3. найди остаток;
4. проверь остаток, меньше ли делителя;
5. запиши пример
Во II и III классах надо как можно больше включать разнообразных упражнений на все изученные случаи умножения и деления: примеры в одно и несколько действий, сравнение выражений, заполнение таблиц, решение уравнений и т.д.
№ 14. Понятие составная задача.
Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к разбиению ее на ряд простых задач и последовательному их решению. Таким образом, для решения составной задачи надо установить ряд связей между данными и искомым, в соответствии с которыми выбрать, а затем выполнить арифметические действия.
В решении составной задачи появилось существенно новое сравнительно с решением простой задачи: здесь устанавливается не одна связь, а несколько, в соответствии с которыми выбираются арифметические действия. Поэтому проводится специальная работа по ознакомлению детей с составной задачей, а также по формированию у них умений решать составные задачи.
Подготовительная работа к ознакомлению с составными задачами должна помочь учащимся уяснить основное отличие составной задачи от простой —ее нельзя решить сразу, т. е. одним действием, а для решения надо вычленить простые задачи, установив соответствующие связи между данными и искомым. С этой целью предусматриваются специальные Упражнения: