Умножение многозначного числа на однозначное число.

1) Правило умножения суммы на число учащиеся могут применить самостоятельно к устному умножению многозначных чисел на однозначное, например:

2100·3= (2000 + 100) ·3 = 2000·3+100-·3=6300

5007·4= (5000 + 7) ·4 = 5000·4 + 7·4 = 20028

Переход от устного умножения к письменному строят так, чтобы учащиеся поняли, что сущность вычислительного приема при устном и при письменном умножении на однозначное число одна и та же: используется правило умножения суммы на число, но письменное умножение начинается с низших разрядов, устное — с высших.

2) При ознакомлении с письменным умножением рассматривают пример на умножение трех- или четырехзначного числа на однозначное, где есть переходы через десяток или через сотню.

418·3. Сначала решают способом замены первого множителя суммой разрядных слагаемых и умножают сумму на число:

а) 418·3= (400+10 + 8)-3=400·3+ 10·3 + 8·3= 1200 + 30 + 24=1254

Далее решают пример, переставив разрядные слагаемые:

418·3=(8+10 + 400)·3= 8·3+ 10·3 + 400·3 = 24 +30+1200=1254

3

После этого знакомят с письменным умножением на однозначное число: показывают новую запись столбиком и дает подробное объяснение решения этого же примера. Надо умножить 418 на 3. Записываем второй множитель под единицами первого множителя. Проводим черту. Слева ставим знак умножения «X» (надо пояснить детям, что умножение обозначается не только точкой, но и таким знаком, хотя и здесь можно использовать точку). Начинаем письменное умножение с единиц. Умножаем 8 единиц на 3, получается 24 единицы. Это два десятка и 4 единицы. 4 единицы пишем под единицами, а 2 десятка запомним. 1 десяток умножим на 3, получим 3 десятка, да еще 2 десятка, получим 5 десятков. Пишем их под десятками. 4 сотни умножаем на 3, получим 12 сотен. Это 1 тысяча и 2 сотни. 2 сотни пишем под сотнями и 1 тысячу пишем на месте тысяч. Произведение 1254.

Постепенно переходят к краткому объяснению, опускается название разрядных единиц, например:

4

Надо умножить 578 на 4. Умножаю 8 на 4, получится 32. Два пишу, а 3 запоминаю. 7 умножу на 4, получится 28, да 3. Всего 31; 1 пишу, а 3 запоминаю. Умножаю 5 на 4, получится 20, да 3. Всего 23; записываю 23. Произведение 2312. Можно кратко объяснить и так: четырежды восемь — тридцать два. Два пишу, 3 запоминаю. Четырежды семь — двадцать восемь и т. д.

Запись выполнят и в строчку578·4 = 2312.

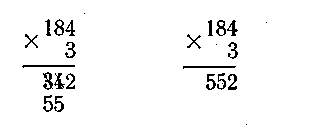В начале изучения темы учитель сообщает, что письменное умножение на однозначное число начинается с единиц, а позднее разъясняют, почему письменное умножение, начинают с низшего, а не с высшего разряда(неудобно приходится зачеркивать ранее записанные цифры) С этой целью решают пример двумя способами:

б) Рассмотрим случаи с нулями в первом множителе. Пусть надо 42300 умножить на 6.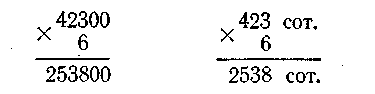

В числе 42 300 содержится 423 сотни. Умножаем 423 сотни на 6, получится 2538 сотен, или 253 800.

в) Умножение однозначного числа на многозначное, используя переместительное свойство

На данном этапе решают примеры на умножение однозначных чисел на многозначные, используя переместительное свойство умножения: 913·6, 4·2836, 7·1230 (136·9, 2836·4, 1230·7).

г) Умножение многозначных чисел, у которых есть нули в конце и середине, используя переместительное свойство

д) Умножение величин, выраженных в метрических единицах.

Примеры решают по-разному: сразу выполнить умножение или сначала заменить составное именованное число простым, выполнить действие над отвлеченными числами и затем простое число заменить составным:

9 т 438 кг 3 28т 314 кг

9 т 438 кг · 3 = 28 т 314 кг 9 т 438 3 28т 314 (кг)

№ 22. ТАБЛИЧНОЕ УМНОЖЕНИЕ

Изучение таблицы умножения является центральной задачей обучения математике во 2 и 3 классе.

К табличному умножению относят случаи умножения однозначных натуральных чисел на однозначные натуральные числа, результаты которых находят на основе конкретного смысла действия умножения (находят суммы одинаковых слагаемых).

Результаты табличного умножения в соответствии с программными требованиями к знаниям, умениям и навыкам дети должны знать наизусть. Умножение с числом нуль, умножение с числами 1 и 10 относят к особым случаям.

Первые приемы составления таблиц умножения связаны со смыслом действия умножения. Результаты этих таблиц получают последовательным сложением одинаковых слагаемых.

Например:

Умножение числа 2

Расположенный рядом рисунок помогает ребенку получить результат пересчетом фигурок. При небольших значениях множителей прием сосчитывания для получения табличного значения произведения вполне приемлем, и учитель им часто пользуется при получении результатов таблиц значений умножения чисел 2, 3, 4. Приведенный пример показывает, что этот прием удобен лишь при небольших значениях второго множителя.

При значении второго множителя больше 5, удобнее использовать для получения результатов табличных значений другой прием: прием прибавления к предыдущему результату.

Например:

Вычисли и запомни:

2• 6 = 2• 5 + 2 = ...

2• 7 = 2• 6 + 2 =...

В учебнике математики для 2 класса этот прием дан более пространно, и поэтому не всегда правильно понимается с точки зрения техники выполнения: 2+2+2+2+2+2 2 • 6

Аналогичным образом составляется таблица значений умножения числа 3.

Следующим приемом, на основе которого составляются таблицы значений умножения чисел, является прием перестановки множителей.

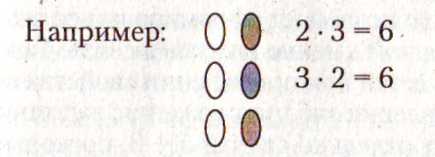Этот прием фактически является первым математическим законом относительно действия умножения в начальной школе: