Производная. Геометрический и физический смысл
Производная
Производная. Геометрический и физический смысл
Определение.Производной функции у = f(x) в точке х = х0 называется предел отношения приращения функции 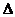 у = f(x0 +
у = f(x0 + 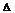 x) – f(x0) к приращению аргумента
x) – f(x0) к приращению аргумента 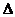 х = (х0+
х = (х0+ 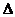 х)-х0, когда последнее стремится к нулю. Обозначается производная функции y’ = f’(x).
х)-х0, когда последнее стремится к нулю. Обозначается производная функции y’ = f’(x).
Итак, имеем
f’(x) = 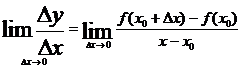
Геометрический смысл
Определение.Производная функции у = f(x) при данном значении аргумента х = х1 равна угловому коэффициенту касательной 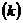 проведенной к графику этой функции в точке, абсцисса которой равна х1:
проведенной к графику этой функции в точке, абсцисса которой равна х1: 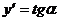 , или
, или 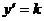
ПРИМЕР 7.Дана кривая 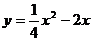 . Найти наклон этой кривой в точке, абсцисса которой равна 6.
. Найти наклон этой кривой в точке, абсцисса которой равна 6.
Решение. Найдем производную этой кривой: 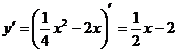 .
.
При х = 6 получим 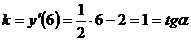 .
.
Физический смысл
Определение.Средняя скорость изменения функции у для промежутка значений аргумента от х до х+ 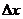 выражается отношением
выражается отношением
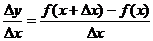
Отношение 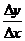 показывает, сколько единиц приращения функции приходится на единицу приращения аргумента.
показывает, сколько единиц приращения функции приходится на единицу приращения аргумента.
Мгновенная (или истинная) скорость изменения функции при данном значении х есть предел, к которому стремится средняя скорость 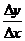 при
при 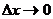 в промежутке изменения аргумента от х до х+
в промежутке изменения аргумента от х до х+ 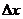 , т.е.
, т.е. 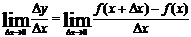
Для линейной функции 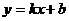 средняя скорость
средняя скорость 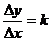 и истинная скорость
и истинная скорость 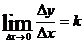 совпадают по величине и численное значение истинной скорости равно коэффициенту k.
совпадают по величине и численное значение истинной скорости равно коэффициенту k.
ПРИМЕР 8. Найти среднюю скорость изменения функции у=3х2 – 6 при изменении х от х1=3 до х2=3,5.
Решение.Найдем приращение аргумента: 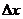 =х2-х1= 3,5 – 3 = 0,5
=х2-х1= 3,5 – 3 = 0,5
Определим значения функции при х2 и х1:У1 = 3*32 – 6 = 21, у2 = 3*(3,5)2 – 6 = 30,75
Вычислим приращение функции: 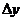 = у2-у1 = 30,75 – 21 = 9,75.
= у2-у1 = 30,75 – 21 = 9,75.
Находим среднюю скорость изменения функции: 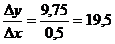 .
.
Основные правила дифференцирования
Если С - постоянное число, u=u(x), v=v(x)- функции, имеющие производные, тогда:
1. 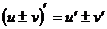
2. 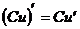
3. 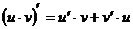
4. 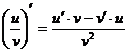
Формулы дифференцирования основных функций
При условии 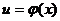 | При условии 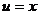 |
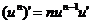 где n – любое действительное число где n – любое действительное число 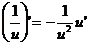 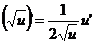 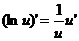 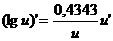 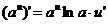 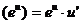 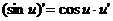 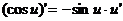 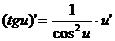 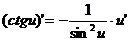 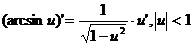 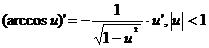 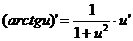 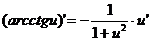 | С’=0 Х’=1 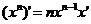 где n – любое действительное число где n – любое действительное число 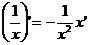 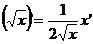 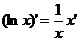 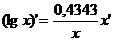 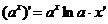 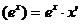 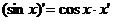 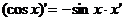 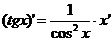 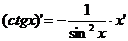 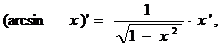 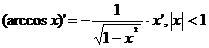 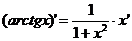 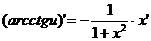 |
ПРИМЕР 9. Найти производные функций: 1) f(x) = 5 + x3 + 3x2 + sin x + 2tg x; 2) f(x) = 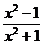 ; 3) f(x) = x sin x.
; 3) f(x) = x sin x.
Решение.
1) f ‘ (x) = (5 + x3 + 3x2 + sin x + 2tg x) ‘ = (5)’ + (x3 )’+ (3x2 )’+ (sin x)’ + (2tg x)’ = = 3x2 + 6x + cos x + 2 / cos2x
2) f ‘ (x) = ( 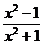 )’=
)’= 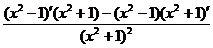 =
= 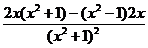 = =
= = 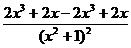 =
= 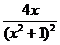
3) f ‘(x) = (x sin x)’ = (x )’sin x + (sin x)’ x = 1*sin x + x cos x = sin x + x cos x.
ПРИМЕР 10.Найти производную функции: 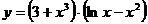
Решение. 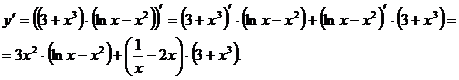
Производные обратных тригонометрических функций
ПРИМЕР 11. Найти производную функции f(x) = arcsin 2x, вычислить f ‘(-1/4).
Решение.
f ' (x) = (arcsin 2x)’= 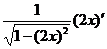 =
= 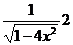 =
= 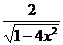
f ‘ (-1/4) = 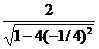 =
= 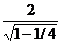 =
= 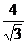
ПРИМЕР 12.Найти производную функции: 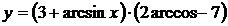
Решение.
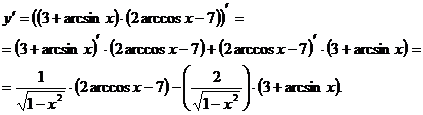
Производная сложной функции
Если имеется сложная функция у = f [ h(x) ], то yx’ = fh’(h) * hx’(x) – производная сложной функции.
ПРИМЕР 13. Найти производные сложных функций: 1) f (x) = cos 6 (3x2 – 5);
2) f (x) = ln ( x - 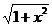 ).
).
Решение.
1) Если обозначим функцию cos (3x2 – 5) = u, то для нахождения производной используем формулу 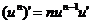 , где n=6, тогда получим
, где n=6, тогда получим
f ‘(x) = (cos6 (3x2 – 5))’ = 6× cos 5 (3x2 – 5) × (cos (3x2 – 5))’
Теперь обозначим 3x2 – 5 = t и воспользуемся формулой 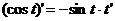 , получим
, получим
(cos (3x2 – 5))’ = -sin(3x2 – 5) × (3x2 – 5)’ = -sin(3x2 – 5) × 6x, подставим в искомую производную функции:
f ‘(x) = 6 × cos 5 (3x2 – 5) × (-sin(3x2 – 5)) × 6x = - 36x × cos 5 (3x2 – 5) × sin(3x2 – 5)
2) Аналогично рассмотренному примеру обозначим x - 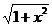 = u , тогда
= u , тогда
f ‘(x) = 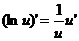 , получим
, получим
f ‘(x) = [ln ( x - 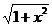 )]’=
)]’= 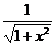 (х -
(х - 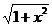 )’ =
)’ = 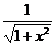 × (1 – (
× (1 – ( 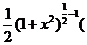 1+x2)’)=
1+x2)’)=
= 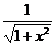 ×(1 –
×(1 – 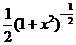 × 2x )=
× 2x )= 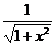 ×
× 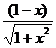 =
= 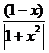
Производные высших порядков
Производная f ‘(х) называется производной первого порядка. Производная от f ‘(x) называется производной второго порядка (или второй производной) от функции f(x) и обозначается y `` или f ``(x). Производная от f ``(x) называется производной третьего порядка (или третьей производной) от функции f (x) и обозначается y``` или f ```(x) и т.д.
Производная n – го порядка есть производная от производной (n – 1)-го порядка, т.е. 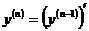 .
.
Производные начиная со второго порядка называются производными высшего порядка.
ПРИМЕР 14. Найти производную второго порядка от функции y = tg x
Решение.
y ` = (tg x)` = 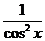
y `` = ( 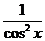 )` =
)` = 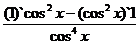 =
= 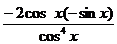 =
= 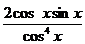 =
= 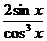
Интегральное исчисление
Таблица основных интегралов
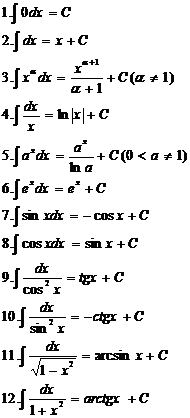
ПРИМЕР 20. Найти следующие интегралы а) 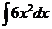
Решение. Используя свойства и формулы интегрирования, получим
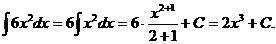
Проверка: d(2x3+C)=6x2dx. Получили подынтегральное выражение; следовательно, интеграл найден правильно.
б) 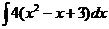
Решение. Используя свойства 30 и 40 и формулы таблицы интегралов, имеем 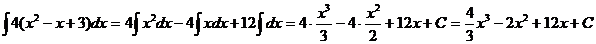 . Постоянная интегрирования С равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную
. Постоянная интегрирования С равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную
(С1+С2+С3=С).
Вопросы самоконтроля:
1.Дать определение неопределенного интеграла.
2.Что называется первообразной функции?
3.Перечислите основные свойства интегралов.
Методы интегрирования
Метод подстановки
ПРИМЕР 22. Вычислить интеграл 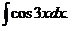
Решение. Интеграл не табличный. Применим подстановку t = 3x, тогда 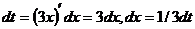 . Подставив в интеграл получаем:
. Подставив в интеграл получаем:
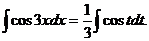 - табличный интеграл. Применяя формулу таблицы основных интегралов, находим
- табличный интеграл. Применяя формулу таблицы основных интегралов, находим 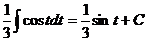 . Возвращаясь к переменной х, окончательно получаем
. Возвращаясь к переменной х, окончательно получаем 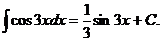
3. Интегрирование по частям:Используем формулу 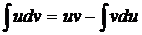
ПРИМЕР 23. Найти следующие интегралы:
а) 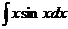
Решение. Положим u=x, dv=sinxdx; тогда du=dx, 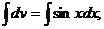 т.е. v=-cosx. Используя формулу (11.14), получим
т.е. v=-cosx. Используя формулу (11.14), получим 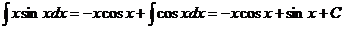 .
.
б) 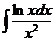
Решение. Положим u=lnx, 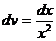 ; тогда
; тогда 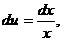
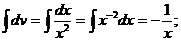
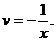 По формуле (11.14) получим
По формуле (11.14) получим 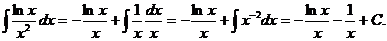
Вопросы и задания для самопроверки:
1. Объяснить в чем заключается метод замены переменной.
2. Напишите формулу интегрирования по частям.
3. Вычислите интеграл
Определенный интеграл
Определение. Определенным интегралом от функции f(x) на отрезке 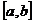 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю.
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю.
Для вычисления определенного интеграла служит формула Ньютона – Лейбница, где определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
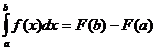 - формула Ньютона – Лейбница
- формула Ньютона – Лейбница
ПРИМЕР 24. Вычислить интегралы
а) 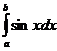
Решение. Так как одной из первообразных для функции f(x) = sin x является функция F(x) = -cos x, то применяя формулу Ньютона – Лейбница, получаем
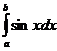 =
= 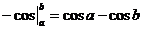
б) 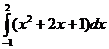 .
.
Решение. По формуле Ньютона – Лейбница получаем. 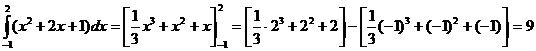 .
.
в) 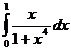
Решение.Воспользуемся методом подстановки
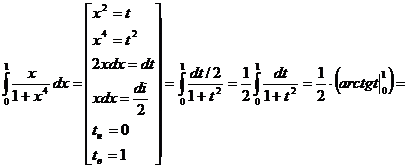
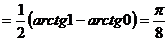
Вопросы и задания для самоконтроля:
1.Дайте определение определенного интеграла.
2.Как выглядит формула Ньютона – Лейбница.
3.Вычислить интеграл 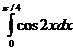
Производная
Производная. Геометрический и физический смысл
Определение.Производной функции у = f(x) в точке х = х0 называется предел отношения приращения функции 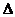 у = f(x0 +
у = f(x0 + 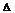 x) – f(x0) к приращению аргумента
x) – f(x0) к приращению аргумента 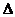 х = (х0+
х = (х0+ 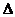 х)-х0, когда последнее стремится к нулю. Обозначается производная функции y’ = f’(x).
х)-х0, когда последнее стремится к нулю. Обозначается производная функции y’ = f’(x).
Итак, имеем
f’(x) = 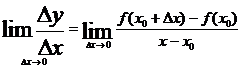
Геометрический смысл
Определение.Производная функции у = f(x) при данном значении аргумента х = х1 равна угловому коэффициенту касательной 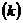 проведенной к графику этой функции в точке, абсцисса которой равна х1:
проведенной к графику этой функции в точке, абсцисса которой равна х1: 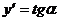 , или
, или 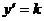
ПРИМЕР 7.Дана кривая 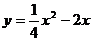 . Найти наклон этой кривой в точке, абсцисса которой равна 6.
. Найти наклон этой кривой в точке, абсцисса которой равна 6.
Решение. Найдем производную этой кривой: 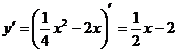 .
.
При х = 6 получим 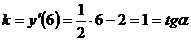 .
.
Физический смысл
Определение.Средняя скорость изменения функции у для промежутка значений аргумента от х до х+ 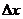 выражается отношением
выражается отношением
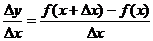
Отношение 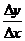 показывает, сколько единиц приращения функции приходится на единицу приращения аргумента.
показывает, сколько единиц приращения функции приходится на единицу приращения аргумента.
Мгновенная (или истинная) скорость изменения функции при данном значении х есть предел, к которому стремится средняя скорость 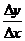 при
при 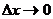 в промежутке изменения аргумента от х до х+
в промежутке изменения аргумента от х до х+ 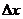 , т.е.
, т.е. 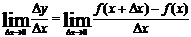
Для линейной функции 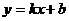 средняя скорость
средняя скорость 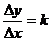 и истинная скорость
и истинная скорость 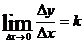 совпадают по величине и численное значение истинной скорости равно коэффициенту k.
совпадают по величине и численное значение истинной скорости равно коэффициенту k.
ПРИМЕР 8. Найти среднюю скорость изменения функции у=3х2 – 6 при изменении х от х1=3 до х2=3,5.
Решение.Найдем приращение аргумента: 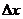 =х2-х1= 3,5 – 3 = 0,5
=х2-х1= 3,5 – 3 = 0,5
Определим значения функции при х2 и х1:У1 = 3*32 – 6 = 21, у2 = 3*(3,5)2 – 6 = 30,75
Вычислим приращение функции: 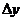 = у2-у1 = 30,75 – 21 = 9,75.
= у2-у1 = 30,75 – 21 = 9,75.
Находим среднюю скорость изменения функции: 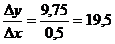 .
.
