Теория функций комплексного переменного
1. Разложить функцию 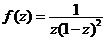 в ряд Лорана в кольцах
в ряд Лорана в кольцах
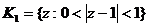 и
и 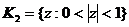
2. Исследовать характер изолированных особых точек функции 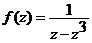 , включая и точку
, включая и точку 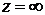 . Найти вычеты функции f в этих точках.
. Найти вычеты функции f в этих точках.
3. C помощью теории вычетов вычислить интеграл
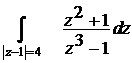 .
.
4. Построить дробно-линейное отображение w(z) круга 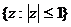
на полуплоскость 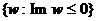
Функциональный анализ и интегральные уравнения
- Пусть m – мера Лебега на
 R. Найти
R. Найти
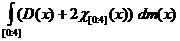 , где D(x) – функция Дирихле,
, где D(x) – функция Дирихле, 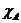 - характеристическая функция множества А.
- характеристическая функция множества А.
- Проверить, является ли последовательность
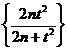 точек метрического пространства С[0;1] сходящейся, фундаментальной.
точек метрического пространства С[0;1] сходящейся, фундаментальной.
- Является ли оператор
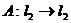 , действующий по формуле
, действующий по формуле
Ax = (2x2, 2x3, …, 2xn, …) линейным, ограниченным? Если да, то найти его норму.
- Пусть
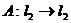 , действующий по формуле Ax = (x1, x2, 5x3,0,…). Найти спектр этого оператора.
, действующий по формуле Ax = (x1, x2, 5x3,0,…). Найти спектр этого оператора.
5. Найти сопряжённый оператор к оператору
A: L 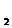 [0;1]
[0;1] 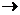 L
L 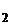 [0;1], если (Ax)(t) =
[0;1], если (Ax)(t) = 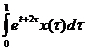 .
.
- Определить, при каких значениях
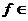 L
L 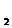 [0;1] уравнение
[0;1] уравнение
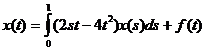 имеет решение в пространстве L
имеет решение в пространстве L 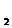 [0;1].
[0;1].
Теория вероятностей и математическая статистика
1. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей, когда он будет тащить первым или вторым?
2. Среди 25 экзаменационных билетов 5 "хороших". Два студента по очереди берут по одному билету. Найти вероятность следующих событий:
A = {первый студент взял "хороший" билет};
В = {второй студент взял "хороший" билет};
C = {оба студента взяли "хорошие" билеты}.
3. На отрезок АВ длины 3 наудачу брошено пять точек. Найти вероятность того, две точки будут находиться от точки А на расстоянии, меньшем 2, а три – на расстоянии, большем 2.
4. В партии из 10 деталей содержится 3 нестандартных. На удачу отобраны 2 детали. Найти математическое ожидание и дисперсию числа нестандартных деталей среди отобранных.
5. Плотность распределения вероятностей абсолютно непрерывной случайной величины 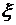 имеет форму
имеет форму
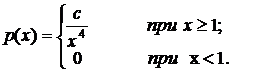
Найти константу с, функцию распределения и дисперсию 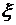 .
.
Алгебра и теория чисел
1. Исследовать систему на совместимость и решить методом Крамера.
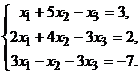
2. Решить систему линейных алгебраических уравнений методом Гаусса

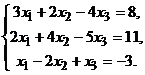 .
.
3. Разложить пространство R4 на прямую сумму подпространств размерности 2.
4. Докажите, что в пространстве M(2, R) система векторов 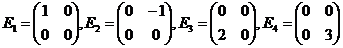 линейно независима.
линейно независима.
5. Найдите жорданову нормальную форму матриц: 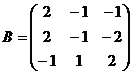 .
.
6. Исследовать, являются ли векторы
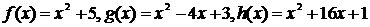
векторного пространства 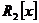 линейно зависимыми.
линейно зависимыми.
7. Найти собственные значения и собственные векторы линейного оператора пространства R2, заданного в некотором базисе матрицей
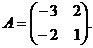 .
.
8. Найти все значения 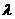 , при которых вектор
, при которых вектор 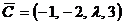 линейно выражается через векторы
линейно выражается через векторы
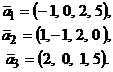
9. Найти базис и размерность линейной оболочки 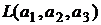 векторов из
векторов из 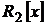 , где
, где 
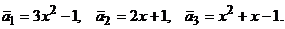
10. Докажите, что линейные пространства 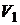 и
и 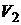 изоморфны:
изоморфны:
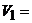 C над R ,
C над R , 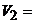 R2.
R2.
11. Найти матрицу, обратную матрице А
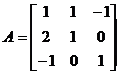 .
.
12. Вычислить: а) 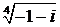 ; б)
; б) 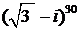 .
.
13. С помощью алгоритма Евклида найти наибольший общий делитель (96,165) и выразить его через исходные числа.
14. Составить таблицы сложения и умножения в кольце классов вычетов 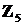 .
.
15. Даны два базиса 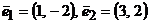 и
и 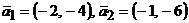 пространства
пространства 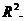
Найти матрицу перехода от базиса 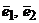 к
к 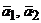 .
.
16. Найти ранг матрицы А
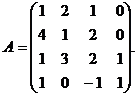
Аналитическая геометрия
1. Вычислите длины диагоналей параллелограмма, построенного на векторах 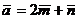 и
и 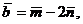 где
где 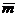 и
и 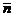 – единичные векторы, угол между которыми 600.
– единичные векторы, угол между которыми 600.
2. Вычислите площадь параллелограмма, диагонали которого определяют векторы 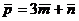 и
и 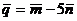 , если
, если 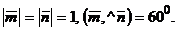
3 .Составьте уравнение прямой, проходящей через точку А (12, 6) так, чтобы площадь треугольника, образованного ею и координатными осями, была равна 150 кв. ед.
4. Найдите основание перпендикуляра, проведенного из точки А (1, 3, 5) к прямой, по которой пересекаются плоскости 2x + 2y + z – 1 = 0,
3x + y +2z – 3 = 0.
5. Найдите расстояние между скрещивающимися прямыми:
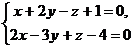 и
и 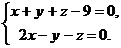
6. Через прямую x = 2 + 5t, y = 3 + t, z = –1 + 2t проведите плоскость, перпендикулярную к плоскости 4x + 3y – z + 3 = 0.
7. Какая плоская фигура задана уравнением:
x2 – 4y2 + 4x + 24y – 36 = 0.
