Исследование функции на монотонность с помощью производной.

Если x₂>x₁, f(x₂)>f(x₁), то ф-ция монотонно возрастает

Если x₂>x₁, f(x₂)<f(x₁), то ф-ция монотонно убывает

Монотонность - постоянство

Необходимые признаки:1)если ф-ция f(x) всюду в интервале возрастает, то ее производная в этом интервале неотрицательна (f`(x)>=0)

2)если ф-ция f(x) всюду в интервале убывает, то ее производная в этом интервале неположительная (f`(x)<=0)

3)если ф-ция f(x) всюду в интервале постоянна, то ее производная в этом интервале =0 (f`(x)=0)

Достаточные признаки монотонности: 1)если f`(x) в интервале положительна, то ф-ция f(x) возрастает в этом интервале.

2)если f`(x)<0, то ф-ция f(x) возрастает в этом интервале.

3)если f`(x)=0, то ф-ция f(x)=const на интервале.

x₁<a<x₂, x₂-x₁>0, x₂>x₁

1. если f`(a)>0, то f(x₂)>f(x₁)

2. если f`(a)<0, то f(x₂)<f(x₁)

3. если f`(a)=0, то f(x₂)=f(x₁)

Точки экстремума функции. Признаки точек экстремума

Точка х называется точкой max ф-ции, если значение ф-ции в этой точке - наименьшее в некоторой ее окрестности.

1- локальный max

2- локальный min

3- глобальный max

4- глобальный min

если tga>0, то f`(x)>0

если tga<0, то f`(x)<0

Необходимый признак экстремума: ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.

(В них можно построить ¥ касательных).

Достаточный признак: точка х₀ является точкой экстремума, если ее производная в этой точке меняет знак:

- если с “+” на “-”, то х₀- т. max

- если с “-” на “+”, то х₀- т. min

Выпуклость и вогнутость графика функции. Точки перегиба.

Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.

Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.

Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0

Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая

Признаки точки перегиба: чтобы X₀ была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х₀.

Схема исследования функции. Показать на примере.

Найти:
-обл. определения ф-ции

-точки разрыва и интервалы, где ф-ция явл-ся непрерывной

-поведение ф-ции в окрестностях точки разрыва, вертикальной асимптоты

-т. пересечения графика с осями координат

-симметрия графика (чет./нечет):

f(-x)=x симметрична относительно осей

f(-x)=-x симметрична относительно О(0,0)

-периодичность

-интервалы монотонности

-точки экстремума

-наибольшее и наименьшее значение

-выпуклость, вогнутость

-точки перегиба

-поведение ф-ции в безконечности, наклонная и горизонтальные асимптоты

-нанесение на график.

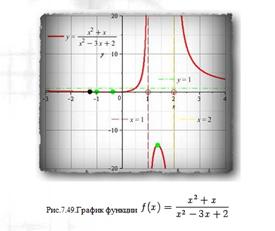
Пример 1

Исследовать и построить график функции

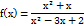
1). Заметим, что знаменатель имеет корни 1 и2, так что функцию можно представить в виде

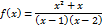
Т.к. , отсюда следует, что области определения функции

2)Определим тип функции, т.е. четная,нечетная или общего вида функция.

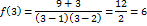
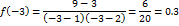
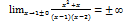
3) 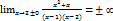,следовательно x=1 и x=2 является точкой разрыва II рода, что в свою очередь

Даёт нам две вертикальные ассимптоты.

4)С ox: y=0

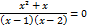
C oy: x=0

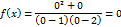
Пользуясь методом интервалов (известным из школьной программы), определим знак функции на интервалах между корнями и точками разрыва. Таких интервалов получается пять: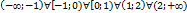

На этом рисунке знаком + отмечены те интервалы, на которых функция положительна, и знаком - те, где она отрицательна.

5) Найдём производную:

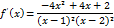
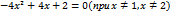
Решением квадратного неравенства служит интервал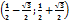

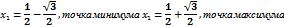
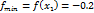
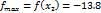
6) Найдём вторую производную:

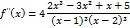
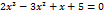
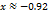
7)Построение графика.